1. 关于 GAMES 201 课程
- 课程简介:本课程将会介绍基于物理的动画(Physically based animation)的基础和前沿知识,从拉格朗日、欧拉、混合欧拉-拉格朗日三大视角,介绍刚体、布料、烟雾、液体、弹塑性体(雪、泥沙、果冻、橡皮泥等)的模拟。通过本课程的学习,配合Taichi编程语言的使用,同学们可以独立从零开始编写最先进的高性能影视级物理求解器,并且利用自己的渲染器生成自己的特效动画。
- 课程内容:Taichi语言基础、刚体、液体、烟雾、弹塑性体、PIC/FLIP法、Krylov-子空间求解器、预条件、无矩阵法、多重网格、弱形式与有限元、隐式积分器、辛积分器、拓扑优化、带符号距离场、自由表面追踪、物质点法、大规模物理效果渲染、现代处理器微架构、内存层级、并行编程、GPU编程、稀疏数据结构、可微编程…
物理引擎(Physics Engine):A physics engine is computer software that provides an approximate simulation of certain physical systems, such as rigid body dynamics (including collision detection), soft body dynamics, and fluid dynamics, of use in the domains of computer graphics, video games and film.
Keywords: Discretization(离散化), Efficient Solvers(高效率求解器), Productivity(提高生产力), Performance(性能), Hardware Architecture(硬件架构), Data Structures(数据结构), Parallelization(并行化), Differentiability(可微性).
1.1. Taichi 编程语言 简洁介绍
Taichi 是一个嵌入在python的高性能领域特定的语言。
- 设计初衷自娱提高计算机图形学应用的生产力和可移植性
- 数据导向、并行、megakernels(将多个小内核合并成一个更大的内核,以减少内核启动的开销并优化硬件资源利用率)
- 将数据结构从计算中解耦(decouple)
- 以密集方式访问空间稀疏张量
- 可微分编程支持
1.2. 环境搭建
在 python 环境下按如下指令搭建即可:
pip install taichi加载 demo gallery
ti gallery1.3. 初始化
在使用 taichi 前,一定要先初始化 taichi
ti.init(arch=ti.gpu)最频繁使用的参数:arch
ti.x64/arm/cuda/vulkan/opengl/metal:指定使用某个后端;ti.cpu:(默认),自动检测x64/armCPUs;ti.gpu:按顺序尝试使用ti.cuda/vulkan/opengl/metal,如果没有可用的 GPU 架构,会使用 CPU。
1.4. 数据类型
Taichi 是强类型(Strongly Typed,显式类型声明、严格类型检查、限制隐式转换),支持如下基本类型:
- Signed integers:ti.i8/i16/i32/i64
- Unsigned integers:ti.u8/u16/u32/u64
- Float-point numbers:ti.f32/f64
最常用:ti.i32 and ti.f32,布尔值用 ti.i32 表示。
在 Taichi 中,tensors(张量)是 first-class citizens(某种数据类型或对象能够像其他数据类型一样被平等地使用、传递、赋值、返回和操作)。
- 张量本质上是多维数组
- 张量的元素可以是标量(
var),向量(ti.Vector),或矩阵(ti.Matrix) - 张量的元素总是通过
a[i,j,k]语法来访问(没有指针!)。 - 访问越界会导致未定义行为
- (高级)张量可以是空间稀疏的
- 尽管数学上矩阵被视为 2D 张量,但在 Taichi 中,张量和矩阵是两个完全不同的概念,矩阵可以作为张量元素使用。
tensor 使用示例:
import taichi as ti
ti.init()
a = ti.var(dt=ti.f32, shape=(42, 63)) # A tensor of 42x63 scalars
b = ti.Vector(3, dt=ti.f32, shape=4) # A tensor of 4x3D vectors
c = ti.Matrix(2, 2, dt=ti.f32, shape=(3, 5)) # A tensor of 3x5 2x2 matrices
loss = ti.var(dt=ti.f32, shape=()) # A (0-D) tensor of a single scalar
a[3, 4] = 1
print('a[3, 4] =', a[3, 4]) # "a[3, 4] = 1.000000"
b[2] = [6, 7, 8]
print('b[0] =', b[0][0], b[0][1], b[0][2])
loss[None] = 3
print(loss[None]) # 31.5. 计算
1.5.1. kernel 和 function
在 Taichi 中,计算位于(reside)内核(kernel),kernel 无法调用 kernel。
- Taichi 内核和函数使用的语言类似于 Python
- Taichi 内核语言是 compiled(编译型),statically-typed(静态类型的),lexically-scoped(词法作用域的),parallel(并行)和 differentiable(可微分)
- 内核必须使用
@ti.kernel修饰,这样内核才会被标记并编译 - 内核的参数和返回值必修进行 type-hinted 类型提示(比如 ti.i32)
示例:
@ti.kernel
def hello(i: ti.i32):
a = 40
print('Hello world!', a + i)
hello(2) # "Hello world! 42"
@ti.kernel
def calc() -> ti.i32:
s = 0
for i in range(10):
s += i
return s # 45Taichi 函数可以由 Taichi 内核和其他 Taichi 函数调用。它们必须使用 @ti.func 装饰器。(Taichi 中内核和函数的区别:Python 可以直接调用 kernel 但不能直接调用 function)
示例:
@ti.func
def triple(x):
return x * 3
@ti.kernel
def triple_array():
for i in range(128):
a[i] = triple(a[i])- Taichi 函数会被强制内联,当前不支持递归(2020)
- Taichi 函数最多只能包含一个返回语句
1.5.2. 数学计算
大部分 Python 的数学运算函数在 Taichi 中均支持,且支持链式比较(chaining comparisons, e.g. a < b <= c != d)。
ti.Matrix仅适用于小矩阵(例如 3×3)。如果需要处理 64×64 的矩阵,应该考虑使用一个 2D 张量来存储标量。ti.Vector和ti.Matrix相同,只不过它只有一列。- 区分元素级(element-wise)乘积
*(会把矩阵 A 和 B 对应位置的元素取出来相乘得到新矩阵)和矩阵乘积@。 - 常见的矩阵操作:
A.transpose() # 转置矩阵
A.inverse() # 求矩阵的逆
A.trace() # 求矩阵的迹(对角线元素之和)
A.determinant(type) # 求矩阵的行列式
A.normalized() # 将矩阵归一化
A.cast(type) # 转换矩阵的数据类型
R, S = ti.polar_decompose(A, ti.f32) # 极分解
U, sigma, V = ti.svd(A, ti.f32) # 奇异值分解(SVD),sigma 是对角矩阵
ti.sin(A)/cos(A) # (元素级)正弦除以余弦1.5.3. 循环
Taichi 中的 for 循环有两种形式:
- 范围循环(Range-for loops):
语法上与 Python 的for循环没有区别,但在 Taichi 内核中最外层作用域 使用时,会被自动并行化。范围循环是可以嵌套使用的。 - 结构循环(Struct-for loops):
用于遍历张量(尤其是稀疏 sparse 张量)中已经分配的元素。(稍后会详细介绍这一点。) - 在 Taichi 内核中,处于最外层作用域的
for循环会自动并行化执行。
Range-for loops 示例:
@ti.kernel
def fill():
for i in range(10): # Parallelized
x[i] += i
s = 0
for j in range(5): # Serialized in each parallel thread
s += j
y[i] = s
@ti.kernel
def fill_3d():
# Parallelized for all 3 <= i < 8, 1 <= j < 6, 0 <= k < 9
for i, j, k in ti.ndrange((3, 8), (1, 6), 9):
x[i, j, k] = i + j + k只有处于最外层作用域的 for 循环才会被并行化,而不是代码中最外层的循环。
@ti.kernel
def foo():
for i in range(10): # ✅ 并行化执行!
...
@ti.kernel
def bar(k: ti.i32):
if k > 42:
for i in range(10): # ❌ 串行执行(因为不在最外层作用域)
...Struct-for 示例:
from taichi import ti
ti.init(arch=ti.gpu)
n = 320
pixels = ti.var(dt=ti.f32, shape=(n * 2, n))
@ti.kernel
def paint(t: ti.f32):
for i, j in pixels: # ✅ 并行遍历所有像素
pixels[i, j] = i * 0.001 + j * 0.002 + t
paint(0.3)
# Struct-for 循环会遍历张量 pixels 中所有的坐标,也就是:(0, 0), (0, 1), (0, 2), ..., (0, 319),(1, 0), ..., (639, 319)1.5.4. 原子操作
在 Taichi 中,增强赋值操作(例如 x[i] += 1)会自动执行为 原子操作,以确保并行环境下数据安全。
当你在并行环境中修改全局变量时,务必使用原子操作,否则结果将是错误的。例如,想要对张量 x 中所有元素求和:
@ti.kernel
def sum():
for i in x:
# 方法 1:正确,使用 +=,自动原子操作
total[None] += x[i]
# 方法 2:正确,显式使用 atomic_add
ti.atomic_add(total[None], x[i])
# 方法 3:❌ 错误,非原子操作,可能导致结果错误
total[None] = total[None] + x[i]1.5.5. Taichi-scope v.s. Python-scope
- Taichi 作用域(Taichi-scope):
所有被@ti.kernel或@ti.func装饰的代码。 - Python 作用域(Python-scope):
所有在 Taichi 作用域之外的普通 Python 代码。 - Note:
- Taichi 作用域 中的代码会被 Taichi 编译器编译,并在 并行设备上执行(如 GPU 或 CPU 多线程)。
- Python 作用域 中的代码是普通的 Python 代码,由 Python 解释器 逐行执行。
1.5.6. Taichi 程序的执行阶段(Phases)
- 初始化阶段(Initialization):
ti.init(…) - 张量分配阶段(Tensor Allocation):
ti.var, ti.Vector, ti.Matrix - 计算阶段(Computation)(启动内核,在 Python 作用域中访问张量):在初次加载一个 kernel 或在 Python-scope 访问一个 tensor 的时候会从张量分配阶段转向计算阶段,此时无法再分配新的张量(2020)
- (可选)重置阶段(Optional Reset):重置 Taichi 状态(清除所有已分配的张量和内核,释放内存):
ti.reset()
1.5.7. 综合示例:fractal.py
import taichi as ti
ti.init(arch=ti.gpu)
n = 320
pixels = ti.var(dt=ti.f32, shape=(n * 2, n))
@ti.func
def complex_sqr(z):
return ti.Vector([z[0] ** 2 - z[1] ** 2, z[1] * z[0] * 2])
@ti.kernel
def paint(t: ti.f32):
for i, j in pixels: # 并行绘制所有像素
c = ti.Vector([-0.8, ti.cos(t) * 0.2])
z = ti.Vector([i / n - 1, j / n - 0.5]) * 2
iterations = 0
while z.norm() < 20 and iterations < 50:
z = complex_sqr(z) + c
iterations += 1
pixels[i, j] = 1 - iterations * 0.02
gui = ti.GUI("Julia Set", res=(n * 2, n))
for i in range(1000000):
paint(i * 0.03)
gui.set_image(pixels)
gui.show()1.6. Debug mode
以 debug mod 初始化 Taichi:ti.init(debug=True, arch=ti.cpu) ,启用越界检查(仅限 CPU 后端)。
示例:
import taichi as ti
ti.init(debug=True, arch=ti.cpu)
a = ti.var(ti.i32, shape=(10))
b = ti.var(ti.i32, shape=(10))
@ti.kernel
def shift():
for i in range(10):
a[i] = b[i + 1] # 在 Runtime error in debug mode
shift()Python 代码格式化可以使用 yapf
2. 拉格朗日视角(1):Mass-Spring System and SPH
2.1. Lagrangian v.s. Eulerian: Two Views of Continuums(连续体)
- Lagrangian(拉格朗日视角)
- 核心思想:跟踪每一个粒子(或质点)随时间的运动和状态变化。
- 像是“坐在物体上观察世界”。
- 常用于:固体力学、粒子方法(如 MPM、SPH)。
- 例子:追踪一滴水的路径,从出发点到当前位置。
- Eulerian(欧拉视角)
- 核心思想:固定在空间的某个位置,观察有多少粒子经过这里,它们的速度、密度、压力等如何变化。
- 像是“站在原地看物体经过你”。
- 常用于:传统流体模拟(如基于网格的 Navier-Stokes 解法)。
- 例子:在河边观察水流经过你的位置。
2.2. Mass-Spring Systems(弹簧质点系统)
2.2.1. Force Formulation(力学建模)
Hooke’s Law: \[\mathbf{f}_{ij} = -k(\|\mathbf{x}_i – \mathbf{x}_j\|_2 – l_{ij})(\widehat{\mathbf{x}_i – \mathbf{x}_j})\]
\[\mathbf{f}_i = \sum\limits_j^{j \ne i}\mathbf{f}_{ij}\]
Newton’s second law of motion: \[\frac{\partial \mathbf{v}_i}{\partial t} = \frac{1}{m_i}\mathbf{f}_i\]
\[\frac{\partial \mathbf{x}_i}{\partial t} = \mathbf{v}_i\]
- \(k\):弹簧刚度(spring stiffness)
- \(l_{ij}\):粒子 \(i\) 和粒子 \(j\) 之间弹簧的原长(spring rest length)
- \(m_i\):粒子 \(i\) 的质量(mass of particle \(i\))
- \(\widehat{\mathbf{x}_i – \mathbf{x}_j}\):从粒子 \(j\) 指向粒子 \(i\) 的方向向量
- \(\widehat{□}\):表示单位化(归一化,normalization),即方向向量的归一版本(单位向量)
2.2.2. Time integration(时间积分)
- Forward Euler(explicit,显式欧拉)\[\mathbf{v}_{t+1} = \mathbf{v}_{t} + \Delta t \frac{\mathbf{f}_{t}}{m}\]\[\mathbf{x}_{t+1} = \mathbf{x}_{t} + \Delta t \mathbf{v}_{t}\]
- Semi-implicit Euler(aka. symplectic Euler, explicit,半隐式欧拉)\[\mathbf{v}_{t+1} = \mathbf{v}_{t} + \Delta t \frac{\mathbf{f}_{t}}{m}\]\[\mathbf{x}_{t+1} = \mathbf{x}_{t} + \Delta t \mathbf{v}_{t+1}\]
- Backward Euler(often with Newton’s method, implicit,隐式欧拉,需迭代求解)
简单实现示例(基于 Semi-implicit Euler):计算新速度,与地面碰撞,计算新位置
@ti.kernel
def substep():
n = num_particles[None]
# 1. 计算弹簧力 + 阻尼力 + 重力,加速度 -> 更新速度
for i in range(n):
# 阻尼(指数衰减)
v[i] *= ti.exp(-dt * damping[None])
# 初始总力 = 重力
total_force = ti.Vector(gravity) * particle_mass
for j in range(n):
if rest_length[i, j] != 0:
x_ij = x[i] - x[j]
total_force += -spring_stiffness[None] * (x_ij.norm() - rest_length[i, j]) * x_ij.normalized()
# 更新速度
v[i] += dt * total_force / particle_mass
# 2. 与地面碰撞(y 轴下界)
for i in range(n):
if x[i].y < bottom_y:
x[i].y = bottom_y
v[i].y = 0
# 3. 更新位置
for i in range(n):
x[i] += v[i] * dt2.2.3. 显式 v.s. 隐式 时间积分器(time integrators)
- 显式方法(Explicit)如:Forward Euler、Symplectic Euler、Runge-Kutta(RK) 等
- 未来状态只依赖于过去(无需迭代)
- 实现简单
- 容易“爆炸”(数值不稳定): \[\Delta t \leq c \sqrt{\frac{m}{k}} \quad (c \approx 1)\]即时间步长受限于质量和刚度(适用于弹簧质点等系统)
- 不适合处理高刚度(stiff)材料
- 隐式方法(Implicit)如:Backward Euler、中点法(Midpoint method)等
- 未来状态依赖于过去与未来自身
- 存在“先有鸡还是先有蛋”的问题 —— 需要求解一个线性或非线性方程系统
- 实现相对复杂
- 每一步计算开销更大,但允许使用更大的时间步长(提升整体效率):有时能带来很大收益(如数值稳定性),但并不总是划算
- 存在数值阻尼(Numerical Damping)和锁死现象(Locking)
- 隐式时间积分:\[\mathbf{x}_{t+1} = \mathbf{x}_{t} + \Delta t \mathbf{v}_{t+1}\]\[\mathbf{v}_{t+1} = \mathbf{v}_{t} + \Delta t M^{-1} \mathbf{f}(\mathbf{x}_{t+1})\]
- 消除 \(\mathbf{x}_{t+1}\):\[\mathbf{v}_{t+1} = \mathbf{v}_{t} + \Delta t \mathbf{M}^{-1} \mathbf{f}(\mathbf{x}_{t} + \Delta t \mathbf{v}_{t+1})\]
- 一阶牛顿线性化(First-order Newton Approximation),使用泰勒展开,对力项线性近似(仅用牛顿法的一步):\[\mathbf{v}_{t+1} = \mathbf{v}_{t} + \Delta t \mathbf{M}^{-1} \big[\mathbf{f}(\mathbf{x}_t) + \frac{\partial \mathbf{f}}{\partial \mathbf{x}} (\mathbf{x}_t) \Delta t \mathbf{v}_{t+1}\big]\]
- 整理(Clean up):\[\big[ \mathbf{I} – \Delta t^2 \mathbf{M}^{-1} \frac{\partial \mathbf{f}}{\partial \mathbf{x}} (\mathbf{x}_t) \big] \mathbf{v}_{t+1} = \mathbf{v}_t + \Delta t \mathbf{M}^{-1} \mathbf{f}(\mathbf{x}_t)\]\[\mathbf{A} = \big[ \mathbf{I} – \Delta t^2 \mathbf{M}^{-1} \frac{\partial \mathbf{f}}{\partial \mathbf{x}} (\mathbf{x}_t) \big]\]\[\mathbf{b} = \mathbf{v}_t + \Delta t \mathbf{M}^{-1} \mathbf{f}(\mathbf{x}_t)\]\[\mathbf{A}\mathbf{v}_{t+1} = \mathbf{b}\]得到一个线性系统
- 求解方式:
- Jacobi(实现简单):每一轮使用上一轮的解去更新所有变量
- Gauss-Seidel 迭代法(实现简单):使用最新计算出的值即使更新后续变量
- Conjugate gradients 共轭梯度法
使用 Jacobi 迭代的示例(Demo):
A = ti.var(dt=ti.f32, shape=(n, n)) # 系数矩阵 A
x = ti.var(dt=ti.f32, shape=n) # 当前解向量 x
new_x = ti.var(dt=ti.f32, shape=n) # 下一轮迭代解
b = ti.var(dt=ti.f32, shape=n) # 右侧常数向量 b
@ti.kernel
def iterate():
# 每个维度更新一次
for i in range(n):
r = b[i]
for j in range(n):
if i != j:
r -= A[i, j] * x[j] # 减去非对角项
new_x[i] = r / A[i, i] # 使用对角元素除以得到新值
# 把 new_x 拷贝回 x,准备下一轮
for i in range(n):
x[i] = new_x[i]2.2.4. 统一显式与隐式积分器
\[\big[ \mathbf{I} – \beta \Delta t^2 \mathbf{M}^{-1} \frac{\partial \mathbf{f}}{\partial \mathbf{x}} (\mathbf{x}_t) \big] \mathbf{v}_{t+1} = \mathbf{v}_t + \Delta t \mathbf{M}^{-1} \mathbf{f}(\mathbf{x}_t)\]
- \(\beta = 0\):forward / semi-implicit Euler(explicit)
- \(\beta = 1 / 2\):middle-point(implicit)
- \(\beta = 1\):backward Euler(implicit)
2.2.5. 高效求解思路
如果有巨量的质点和弹簧(如上百万):
- 稀疏矩阵(Sparse matrices):系统中的矩阵非常稀疏,大部分元素为 0,可以用稀疏矩阵存储与计算优化性能。
- 共轭梯度法(Conjugate gradients):一种高效的迭代方法,适用于稀疏、对称正定系统,用于解线性方程组。
- 预条件(Preconditioning):为加速共轭梯度等迭代方法的收敛速度,提升解算器效率。
- 基于位置的动力学(Position-Based Dynamics, PBD):一种稳定性更高、更易并行的动力学近似方法,适合实时布料/柔体模拟。M. Müller et al. (2007). “Position based dynamics”. In: Journal of Visual Communication and Image Representation 18.2, pp. 109–118.
- 快速弹簧质点系统求解器(Fast Mass-Spring System Solver):一种完全不同但更高效的解法,专为大规模模拟设计。T. Liu et al. (2013). “Fast simulation of mass-spring systems”. In: ACM Transactions on Graphics (TOG) 32.6, pp. 1–7.
2.3. 拉格朗日法流体模拟:平滑粒子流体动力学(Smoothed Particle Hydrodynamics, SPH)
高层思想:使用粒子(particles)来携带物理量的采样值,并借助一个核函数 \(W\) 来近似表示连续场(其中 \(A\) 可以是几乎任意随空间变化的物理属性:例如密度(density)、压力(pressure)等,但如果是微分项,则需要用不同的处理方式。)。
\[A(\mathbf{x}) = \sum\limits_{i}A_i \frac{m_i}{\mathbf{\rho}_i} W(\|\mathbf{x} – \mathbf{x}_j\|_2, h)\]
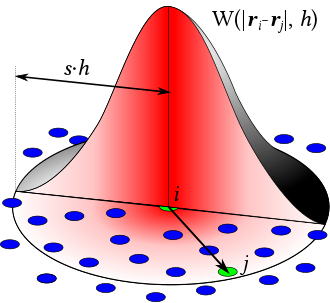
- 最初是为天体物理问题提出的(例如恒星形成、星系碰撞等)。R. A. Gingold and J. J. Monaghan (1977). “Smoothed particle hydrodynamics: theory and application to non-spherical stars”. In: Monthly notices of the royal astronomical society 181.3, pp. 375–389.
- 不需要网格,因此非常适合处理自由液面流动(free-surface flows)(如水花、泼溅等)。J. J. Monaghan (1994). “Simulating free surface flows with SPH”. In: Journal of computational physics 110.2, pp. 399–406.
- 直观上很容易理解:可以把每个粒子想象成一小团水(尽管严格来说并不完全等同)
2.3.1. 使用状态方程(Equation of States, EOS)实现 SPH
也称为弱可压缩 SPH(Weakly Compressible SPH, WCSPH)。M. Becker and M. Teschner (2007). “Weakly compressible SPH for free surface flows”. In: Proceedings of the 2007 ACM SIGGRAPH/Eurographics symposium on Computer animation. Eurographics Association, pp. 209–217.
动量(Momentum)方程:(\(D\):物质导数(粒子关于时间的导数) \(\rho\):密度 \(B\):体积模量(bulk modulus)\(\gamma\):常数,通常 \(\sim 7\))
\[\frac{D\mathbf{v}}{Dt} = -\frac{1}{\rho}\nabla p + \mathbf{g}, \quad p = B\big[\big( \frac{\rho}{\rho_0} \big)^{\gamma} – 1\big]\]\[A(\mathbf{x}) = \sum\limits_{i}A_i \frac{m_i}{\mathbf{\rho}_i} W(\|\mathbf{x} – \mathbf{x}_j\|_2, h), \quad \rho_i = \sum\limits_{j}m_jW(\|\mathbf{x}_i – \mathbf{x}_j\|_2, h)\]
Extras:表面张力(surface tension),粘性项(viscosity);tutorial:D. Koschier et al. (2019). “Smoothed Particle Hydrodynamics Techniques for the Physics Based Simulation of Fluids and Solids”, website.
2.3.2. SPH 中的梯度
\[A(\mathbf{x}) = \sum\limits_{i}A_i \frac{m_i}{\mathbf{\rho}_i} W(\|\mathbf{x} – \mathbf{x}_j\|_2, h)\]\[\nabla A_i = \rho_i \sum\limits_{j}m_j \big(\frac{A_i}{\rho_i^2} + \frac{A_j}{\rho_j^2}\big) \nabla_{\mathbf{x}_i} W(\|\mathbf{x} – \mathbf{x}_j\|_2, h)\]
并不是很准确且无法推导得到,但是至少是对称且动量守恒,能够计算 \(\nabla p_i\),如果不用如上公式,系统容易出现各种各样的不稳定性。
扩展:高阶梯度 Laplace operator (viscosity etc.)…
2.3.3. SPH 模拟循环
回顾动量方程和状态方程:\[\frac{D\mathbf{v}}{Dt} = -\frac{1}{\rho}\nabla p + \mathbf{g}, \quad p = B\big[\big( \frac{\rho}{\rho_0} \big)^{\gamma} – 1\big]\]
- 对于每一个粒子 \(i\),计算 \(\rho_i = \sum\limits_{j} m_jW(\|\mathbf{x}_i – \mathbf{x}_j\|_2, h)\)(注意粒子本身不携带密度,而是通过质量与周围平滑估计)
- 对于每一个粒子 \(i\),使用上述梯度算符计算 \(\nabla p_i\)
- Symplectic Euler step:\[\mathbf{v}_{t+1} = \mathbf{v}_t + \Delta t \frac{D\mathbf{v}}{Dt}, \quad \mathbf{x}_{t+1} = \mathbf{x}_t+\Delta t\mathbf{v}_{t+1}\]
2.3.4. SPH 的变种
- Predictive-Corrective Incompressible SPH(预测-校正不可压缩 SPH,简称 PCI-SPH)
- 改进了传统 WCSPH 的不可压缩性问题(相较于 WCSPH(可以看作显式),更偏向隐式但不完全)
- 通过迭代预测-校正过程逼近严格不可压缩状态
- B. Solenthaler and R. Pajarola (2009). “Predictive-corrective incompressible SPH”. In: ACM SIGGRAPH 2009 papers, pp. 1–6.
- Position-Based Fluids(基于位置的流体,PBF)
- 来源于 Position-Based Dynamics 框架
- 通过位置修正强制保持粒子之间的距离约束,稳定、快速,近年(2020)常用于实时
- Taichi 示例:
ti example pbf2d - M. Macklin and M. Müller (2013). “Position based fluids”. In: ACM Transactions on Graphics (TOG) 32.4, pp. 1–12.
- Divergence-Free SPH(无散度 SPH,DFSPH)
- 基于对速度场施加无散度约束,避免体积损失,适用于高稳定性水体模拟
- 与 PBF 类似,但从速度层面而非位置进行修正
- J. Bender and D. Koschier (2015). “Divergence-free smoothed particle hydrodynamics”. In: Proceedings of the 14th ACM SIGGRAPH/Eurographics symposium on computer animation, pp. 147–155.
- 综述论文(Survey paper):
2.3.5. Courant–Friedrichs–Lewy (CFL) 条件
CFL 条件是数值计算中用于控制时间步长(\(\Delta t\))的稳定性约束,特别适用于显式时间积分方法(explicit integrators),用于解决 stiff 过大时的数值爆炸问题。
公式(用于估算最大稳定时间步长):\[C = \frac{u \Delta t}{\Delta x} \le C_{\text{max}} \sim 1\]
- \(C\):CFL 数(Courant 数)
- \(\Delta t\):时间步长
- \(\Delta x\):空间步长(如粒子半径、网格尺寸等)
- \(u\):最大速度(流场或粒子)
- \(C_{\text{max}}\):稳定性所允许的最大 CFL 数,通常 \(\le 1\)
- CFL 条件用于显式积分法中估计“允许的最大时间步长”,确保仿真在数值上稳定。若违反 CFL 条件,可能导致数值发散或模拟崩溃。常见的 \(C_{\text{max}}\) 推荐值:
- SPH: \(\sim 0.4\)
- MPM: \(0.3 \sim 1\)
- FLIP fluid (smoke): \(1 \sim 5+\)
2.3.6. 加速 SPH:邻居搜索
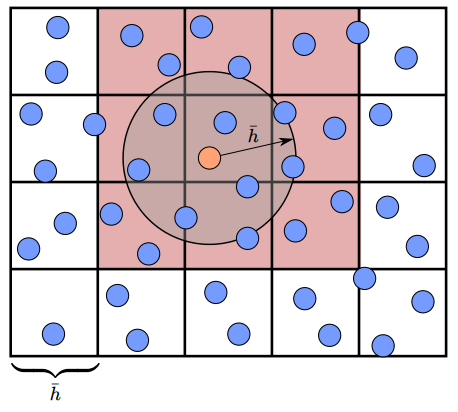
- 目前为止,每一步 SPH 子步骤的时间复杂度是 \(\mathcal{O}(n^2)\),因为每个粒子都要与所有其他粒子计算交互。这种计算成本太高,在实际中不可接受。
- 在实际应用中,通常会构建一种空间数据结构(如体素网格 voxel grid 或哈希表(Compact hashing)),用来加速邻域查找。这样可以显著降低时间复杂度:\(\mathcal{O}(n^2) \rightarrow \mathcal{O}(n)\)
2.3.7. 其他基于粒子的模拟方法
- 离散元方法(Discrete Element Method,DEM)
- 主要用于颗粒材料(如沙子、谷物、粉末)等的模拟
- 每个粒子代表一个实际的固体颗粒,模拟粒子之间的接触力、摩擦、碰撞
- 例如:N. Bell, Y. Yu, and P. J. Mucha (2005). “Particle-based simulation of granular materials”.In: Proceedings of the 2005 ACM SIGGRAPH/Eurographics symposium on Computer animation, pp. 77–86.
- 移动粒子半隐式法(Moving Particle Semi-implicit,MPS)
- 用于不可压缩流体模拟
- 不依赖压力状态方程(不同于 WCSPH),而是通过解一个泊松方程来维持不可压缩性
- S. Koshizuka and Y. Oka (1996). “Moving-particle semi-implicit method for fragmentation of incompressible fluid”. In: Nuclear science and engineering 123.3, pp. 421–434.
- 功率粒子法(Power Particles)
- 一种基于 Power Diagram(幂图) 的不可压缩流体求解器
- 与传统粒子法相比,几何结构更规整,有利于处理边界和物质分布
- F. de Goes et al. (2015). “Power particles: an incompressible fluid solver based on power diagrams.”. In: ACM Trans. Graph. 34.4, pp. 50–1.
- 基于周边动力学的弹簧-质点断裂模拟(A Peridynamic Perspective on Spring-Mass Fracture)
- 引入“周边动力学”(Peridynamics)理论来增强弹簧-质点系统在模拟断裂与裂纹传播方面的能力
- 克服了经典连续力学中微分方程对位移连续性的依赖,可自然处理材料断裂与分离现象
- J. A. Levine et al. (2014). “A peridynamic perspective on spring-mass fracture”. In: Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Citeseer, pp. 47–55.
3. 拉格朗日视角(2):形变、弹性与有限元的基础,Taichi 进阶
- 模拟弹性材料:
- 视觉效果
- 实现难度不高
- 是其他材料模拟的基础(如:黏弹性(viscoelastic)、弹塑性(elastoplastic)、黏塑性(viscoplastic))
3.1. 形变(Deformation)
- 形变映射(Deformation map)\(\boldsymbol{\phi}\):是一个向量到向量的函数,用于描述从参考(静止)材料位置到变形后位置的映射关系:\[\mathbf{x}_{\text{deformed}} = \boldsymbol{\phi} (\mathbf{x}_{\text{rest}})\]
- 形变梯度(Deformation Gradient)\(\mathbf{F}\):\[\mathbf{F} = \frac{\partial \mathbf{x}_{\text{deformed}}}{\partial \mathbf{x}_{\text{rest}}}\]
- 形变梯度的平移不变性(Translational Invariance):两种映射只相差一个常向量偏移,那么它们的形变梯度是相同的。即:形变梯度与整体平移无关,只与相对形变相关。
- 体积比(deform/rest volume ratio)\(J = \text{det}(\mathbf{F})\)(Jacobi Determinante)
3.2. 弹性(Elasticity)
3.2.1. 超弹性(Hyperelasticity)
- 超弹性材料是指其应力-应变关系可以通过一个应变能量密度函数(strain energy density function)来定义的材料,数学形式为:\[\boldsymbol{\psi} = \boldsymbol{\psi}(\mathbf{F})\]
- 其中:\(\boldsymbol{\psi}\):应变能量密度函数,\(\mathbf{F}\):形变梯度
- 直观理解:\(\boldsymbol{\psi}\) 可以被看作一个势能函数,它对材料的形变进行“惩罚”(即能量越高表示形变越大、不自然)。模拟时,系统会试图最小化总能量 \(\boldsymbol{\psi}\),从而实现弹性恢复。
- “应力”(Stress):表示材料内部因变形而产生的弹性力。
- “应变”(Strain):在这里可以近似理解为形变梯度 \(\mathbf{F}\)。
- 注意区分:
- \(\boldsymbol{\psi}\):应变能量密度函数
- \(\boldsymbol{\phi}\):形变映射函数,描述物体从参考状态到当前状态的位置变化
3.2.2. 应力张量(Stress Tensor)
- 应力(stress)描述的是材料内部微小单元之间由于变形而产生的相互作用力,即一个微元对其邻近单元施加的内力密度。
- 应力张量(stress tensor)是一个 \(3 \times 3\) 的矩阵或二阶张量,用于全面描述各方向上的应力分布。在一个给定方向的微小截面上,其单位法向量为 \(\mathbf{n}\),通过应力张量 \(\boldsymbol{\sigma}\) 与 \(\mathbf{n}\) 点乘:\[\text{牵引力(traction)}~ \mathbf{t} = \boldsymbol{\sigma}^T \mathbf{n}\] 可得到该截面上单位面积所受的牵引力(traction vector),即邻近单元施加在该面的内力密度。
- 根据不同的需求会使用不同类型的应力张量:
- 第一类 Piola–Kirchhoff 应力张量(PK1)\[\mathbf{P}(\mathbf{F}) = \frac{\partial \boldsymbol{\psi} (\mathbf{F})}{\partial \mathbf{F}}\]
- 表示参考空间(rest space)中的应力
- 优点:计算简单,广泛用于模拟中
- 缺点:不对称,不守恒动量
- Kirchhoff 应力张量:\(\boldsymbol{\tau}\)
- 一种中间变量,应力张量乘以体积比 J=det(F)J = \det(\mathbf{F})J=det(F) 得到
- 与 Cauchy 应力相关
- Cauchy 应力张量:\(\boldsymbol{\sigma}\)
- 在当前变形空间下定义的真实应力
- 对称张量,因为角动量守恒要求内力对称
- 第一类 Piola–Kirchhoff 应力张量(PK1)\[\mathbf{P}(\mathbf{F}) = \frac{\partial \boldsymbol{\psi} (\mathbf{F})}{\partial \mathbf{F}}\]
- 应力张量间关系:\[\boldsymbol{\tau} = J\boldsymbol{\sigma} = \mathbf{P} \mathbf{F}^T \quad \mathbf{P} = J \boldsymbol{\sigma} \mathbf{F}^{-T}\]
- 直观理解(关于 \(\mathbf{P} = J \boldsymbol{\sigma} \mathbf{F}^{-T}\)):
- \(J\):体积变化因子
- \(\boldsymbol{\sigma}\):真实空间中的应力
- \(\mathbf{F}^{-T}\):将法向量 n\mathbf{n}n 从当前空间变换回参考空间
- 使用 \(\mathbf{F}^{-T}\) 而不是 \(\mathbf{F}^{-1}\),是因为我们在变换的是单位法向量(转置是 \(^{-T}\))而不是点的位置
3.2.3. 弹性模量(Elastic Moduli,针对各向同性材料(isotropic materials))
- 杨氏模量(Young’s modulus)\(E\) \[E = \frac{\sigma}{\varepsilon}\]描述材料抵抗拉伸/压缩变形的能力(应力/应变)。
- 体积模量(Bulk modulus)\(K\) \[K = −V \frac{dV}{dP}\]描述材料抵抗拉伸/压缩变形的能力(应力/应变)。
- 泊松比(Poisson’s ratio)\(\nu\)
- 表示材料在一个方向受拉时,垂直方向的收缩程度
- 取值范围: \(\nu \in [0, 0.5)\)
- 某些“负泊松比材料”(Auxetics)具有 \(\nu \lt 0\),会在拉伸时横向也膨胀。
- Lamé 常数(Lamé parameters)
- 第一 Lamé 常数:\(\lambda\)
- 第二 Lamé 常数:\(\mu\),又称剪切模量(Shear modulus),也常记作 \(G\)
- 常用的转换公式:\[K = \frac{E}{3(1 − 2\nu)} \quad \lambda = \frac{E\nu}{(1 + \nu)(1 – 2\nu)} \quad \mu = \frac{E}{2(1 + \nu)}\]
- 刻画材料习惯于使用杨氏模量和泊松比,因为 Lamé 常数不太直观,一般指定 \(E\) 和 \(\nu\) 后计算得到 \(\lambda\) 和 \(\mu\)。
3.2.4. 超弹性材料模型(Hyperelastic Material Models)
- 线性弹性(Linear elasticity)(仅适用于小变形)
- Neo-Hookean
- \(\boldsymbol{\psi}(\mathbf{F}) = \frac{\mu}{2} \sum_i \big[(\mathbf{F}^T \mathbf{F})_{ii} – 1\big] – \mu \log(J) + \frac{\lambda}{2} \log^2(J)\)
- \(\mathbf{P}(\mathbf{F}) = \frac{\partial \boldsymbol{\psi}}{\partial \mathbf{F}} = \mu (\mathbf{F} – \mathbf{F}^{-T}) + \lambda \log(J) \mathbf{F}^{-T}\)
- (固定)共旋模型(Fixed Corotated)
- \(\boldsymbol{\psi}(\mathbf{F}) = \mu \sum_i (\sigma_i – 1)^2 + \frac{\lambda}{2} (J – 1)^2, \quad \sigma_i \text{ 是 } \mathbf{F} \text{ 的奇异值 }\)
- \(\mathbf{P}(\mathbf{F}) = \frac{\partial \boldsymbol{\psi}}{\partial \mathbf{F}} = 2\mu (\mathbf{F} – \mathbf{R}) + \lambda (J – 1) J \mathbf{F}^{-T}\)
- 详情参考:C. Jiang et al. (2016). “The material point method for simulating continuum materials”. In: ACM SIGGRAPH 2016 Courses, pp. 1–52.
3.3. 有限元基础(Finite Element Method Basics)
有限元方法:Galerkin 离散化方案使用连续偏微分方程(PDE)的弱形式构建离散方程。(课程后续将详细介绍。)
3.3.1. 线性四面体(或三角形)有限元(Linear tetrahedral (triangular) FEM)
线性四面体有限元(用于弹性问题)假设形变映射 \(\boldsymbol{\phi}\) 是仿射(affine)的,因此在单个四面体单元中,变形梯度 \(\mathbf{F}\) 是常数:\[\mathbf{x}_{\text{deformed}} = \mathbf{F}\mathbf{x}_{\text{rest}} + \mathbf{p}\]
对于每个单元 \(e\),其弹性能量为:\[U(e)=\int_e\boldsymbol{\psi}(\mathbf{F}(\mathbf{x})) d\mathbf{x} = V_e\boldsymbol{\psi}(\mathbf{F}_e)\]
问题:如何计算 \(\mathbf{F}_e(\mathbf{x})\)?
3.3.2. 在线性三角形有限元中计算 \(\mathbf{F}_e\)
在二维三角形单元中(对于三维来说是四面体单元),假设顶点的参考位置分别为 \(\mathbf{a_{\text{rest}}}, \mathbf{b_{\text{rest}}}, \mathbf{c_{\text{rest}}}\),而变形后的顶点位置分别为 \(\mathbf{a_{\text{deformed}}}, \mathbf{b_{\text{deformed}}}, \mathbf{c_{\text{deformed}}}\)。由于在线性三角形单元中 \(\mathbf{F}\) 是常数,我们有以下关系: \[ \mathbf{a_{\text{deformed}}} = \mathbf{F a_{\text{rest}}} + \mathbf{p} \tag{1} \] \[ \mathbf{b_{\text{deformed}}} = \mathbf{F b_{\text{rest}}} + \mathbf{p} \tag{2} \] \[ \mathbf{c_{\text{deformed}}} = \mathbf{F c_{\text{rest}}} + \mathbf{p} \tag{3} \] 为了消去 \(\mathbf{p}\): \[ (\mathbf{a_{\text{deformed}}} – \mathbf{c_{\text{deformed}}}) = \mathbf{F} (\mathbf{a_{\text{rest}}} – \mathbf{c_{\text{rest}}}) \tag{4} \] \[ (\mathbf{b_{\text{deformed}}} – \mathbf{c_{\text{deformed}}}) = \mathbf{F} (\mathbf{b_{\text{rest}}} – \mathbf{c_{\text{rest}}}) \tag{5} \] 注意:\(\mathbf{F}_{2 \times 2}\) 包含 4 个线性约束(方程)。 \[ \mathbf{B} = \begin{bmatrix} \mathbf{a_{\text{rest}}} – \mathbf{c_{\text{rest}}} & \mathbf{b_{\text{rest}}} – \mathbf{c_{\text{rest}}} \end{bmatrix}^{-1} \tag{6} \] \[ \mathbf{D} = \begin{bmatrix} \mathbf{a_{\text{deformed}}} – \mathbf{c_{\text{deformed}}} & \mathbf{b_{\text{deformed}}} – \mathbf{c_{\text{deformed}}} \end{bmatrix} \tag{7} \] \[ \mathbf{F} = \mathbf{D} \mathbf{B} \tag{8} \] 注意:矩阵 \(\mathbf{B}\) 在整个物理过程是常数,因此应该预先计算。
3.3.3. 显式线性三角形有限元模拟
回顾半隐式欧拉(Semi-implicit Euler, aka. Symplectic Euler)积分方法:
\[\mathbf{v}_{t+1, i} = \mathbf{v}_{t, i} + \Delta t \frac{\mathbf{f}_{t, i}}{m_i}\] \[\mathbf{x}_{t+1, i} = \mathbf{x}_{t, i} + \Delta t \mathbf{v}_{t+1, i}\]
注意,\(x_{t, i}\) 和 \(v_{t, i}\) 是存储在有限元(如三角形/四面体)的顶点上的。
力的计算公式为:\[\mathbf{f}_{t, i} = -\frac{\partial U}{\partial \mathbf{x}_i} = -\sum_e \frac{\partial U(e)}{\partial \mathbf{x}_i} = -\sum_e V_e \frac{\partial \boldsymbol{\psi}(\mathbf{F})}{\partial \mathbf{F}_e} \frac{\partial \mathbf{F}_e}{\partial \mathbf{x}_i} = -\sum_e V_e \mathbf{P}(\mathbf{F}_e) \frac{\partial \mathbf{F}_e}{\partial \mathbf{x}_i} \]
3.3.4. 隐式线性三角形有限元模拟
回顾 Backward Euler 积分方法:
\[\left[ \mathbf{I} – \Delta t^2 \mathbf{M}^{-1} \frac{\partial \mathbf{f}}{\partial \mathbf{x}}(\mathbf{x}_t) \right] \mathbf{v}_{t+1} = \mathbf{v}_t + \Delta t \ \mathbf{M}^{-1} \mathbf{f}(\mathbf{x}_t) \tag{11}\]
如果希望进行隐式时间积分,需要计算力的导数:\(\frac{\partial \mathbf{f}}{\partial \mathbf{x}} = -\frac{\partial^2 \boldsymbol{\psi}}{\partial \mathbf{x}^2}\)
问题:在显式和隐式方法中,如何计算 \(m_i\)?
可以使用质量集中法(mass lumping)或任何其他方便的方法。
3.4. Taichi 进阶
3.4.1. 目标式面向数据编程(Objective Data-Oriented Programming,ODOP)
Taichi 是一种面向数据编程(Data-Oriented Programming,DOP)的语言,但是单纯的 DOP 会让模块化变得困难。为了提升代码复用性,Taichi 借鉴了一些面向对象编程(Object-Oriented Programming,OOP)的概念。
- 这种混合方案称为目标式面向数据编程(Objective Data-Oriented Programming,ODOP)。
- 三个重要的装饰器:
- 使用
@ti.data_oriented来装饰类; - 使用
@ti.kernel来装饰类中的 Taichi kernel 成员函数; - 使用
@ti.func来装饰类中的 Taichi function 成员函数。
- 使用
3.4.2. 元编程(Metaprogramming)
Taichi 提供了元编程工具。元编程可以:
- 允许用户将几乎任何东西(包括 Taichi 张量)传递给 Taichi kernel;
- 通过将运行时开销转移到编译期来提升运行性能;
- 实现维度无关性(例如同时编写 2D 和 3D 的模拟代码);
- 简化 Taichi 标准库的开发。
Taichi 的 kernel 是延迟实例化(lazily instantiated)的,并且在编译期可以进行大量计算。在 Taichi 中,每一个 kernel 都是模板 kernel,即使它没有模板参数。
模板实例化:Kernel 模板会在第一次调用时实例化,并且会根据相同的模板签名缓存下来,以供后续调用重复使用。
模板参数几乎可以是任何值:可以将张量、类、函数和数值传递给 ti.template() 参数。
模板内核初始化:注意模板内核在初始化时会创造多个内核。
import taichi as ti
ti.init()
@ti.kernel
def hello(i: ti.template()):
print(i)
for i in range(100):
hello(i) # 100 different kernels will be created
@ti.kernel
def world(i: ti.i32):
print(i)
for i in range(100):
world(i) # The only instance will be reused维度无关编程
编译期分支:在 kernel 实例化时提前进行逻辑判断,减少运行期开销(类似 C++17 的 if constexpr)。
enable_projection = True
@ti.kernel
def static():
if ti.static(enable_projection): # 无运行时开销
x[0] = 1强制循环展开:使用 ti.static(range(...)) 在编译期展开循环:
x = ti.Vector(3, dt=ti.i32, shape=16)
@ti.kernel
def fill():
for i in x:
for j in ti.static(range(3)):
x[i][j] = j
print(x[i])
fill()使用 range-for 循环的场景:
- 追求性能
- 用于遍历 vector/matrix 元素。访问矩阵元素的索引必须是编译时常量(compile-time constants)。访问 tensor 时第一维可以是运行时变量,第二维必须是常量,例如:
x[tensor_index][matrix_index]。
变量别名:通过 ti.static 创建简短别名提升可读性。
@ti.kernel
def my_kernel():
a, b, fun = ti.static(tensor_a, tensor_b, some_function)
for i, j in a:
b[i, j] = fun(a[i, j])3.4.3. 可微编程(Differentiable Programming)
前向程序计算 \(f(x)\),可微程序计算 \(\frac{\partial f(x)}{\partial x}\)。
Taichi 支持关于标量损失函数 \(f(x)\) 的反向模式自动微分(AutoDiff),通过反向传播计算梯度。
计算梯度的两种方式:
- 使用 Taichi 的
ti.Tape(loss)同时执行前向与反向传播 - 显式编写梯度 kernel,以获得更灵活的控制
基于梯度的优化示例
目标函数 \(\text{min}_x \ L(\mathbf{x})=\frac{1}{2} \sum^{n-1}_{i=0}(\mathbf{x}_i−\mathbf{y}_i)^2
1. 分配带梯度的张量
x = ti.var(dt=ti.f32, shape=n, needs_grad=True)2. 定义损失函数 kernel
@ti.kernel
def reduce():
for i in range(n):
L[None] += 0.5 * (x[i] - y[i])**23. 使用 ti.Tape(loss=L) 自动执行前向与反向
with ti.Tape(loss=L):
reduce()4. 梯度下降更新
for i in x:
x[i] -= x.grad[i] * 0.13.4.4. 可视化
Taichi 本身支持 2D/3D 的可视化渲染。
4. 欧拉视角下的流体模拟
- 欧拉表示法在空间中使用静态传感器,通常排列成规则的网格/三角形网格。
- 本课程:直观推导 – 而不是有限体积/有限差分。
推荐书目:关于欧拉流体模拟的一本优秀入门书:R. Bridson (2015). Fluid simulation for computer graphics. CRC press.
4.1. 概述
4.1.1. 物质导数(Material Derivatives)
定义:\[\frac{D}{D t} := \frac{\partial}{\partial t} + \mathbf{u} \cdot \nabla\]
E.g.\[\frac{D T}{D t} = \frac{\partial T}{\partial t} + \mathbf{u} \cdot \nabla T\]\[\frac{D \mathbf{u}_x}{D t} = \frac{\partial \mathbf{u}_x}{\partial t} + \mathbf{u} \cdot \nabla \mathbf{u}_x\]
其中 \(\mathbf{u}\) 是物质(流体)速度;该导数也称对流(Advective)导数/拉格朗日导数/粒子导数。
直观上:在材料一部分上的物理量变化 = 时间项 \(\frac{\partial}{\partial t}\) (Eulerian)+ 空间迁移项(材料的运动,随场变化) \(\mathbf{u}\cdot\nabla\)。
4.1.2. (不可压缩)NS方程(Incompressible Navier-Stokes equations)
定义:\[\rho\frac{D \mathbf{u}}{D t} = -\nabla p + \mu \nabla^2 \mathbf{u} + \rho \mathbf{g}, \quad \nabla \cdot \mathbf{u} = 0\]或等价形式:\[\frac{D \mathbf{u}}{D t} = -\frac{1}{\rho}\nabla p + \nu \nabla^2 \mathbf{u} + \mathbf{g}, \quad \nabla \cdot \mathbf{u} = 0\]
其中:\(\mu\) 是动力黏度(Dynamic viscosity),\(\nu = \frac{\mu}{\rho}\) 是运动黏度(Kinematic viscosity)
由三项组成:压强的梯度,黏性相,重力加速度。在计算机图形学中,我们通常忽略黏度项,除非模拟高黏度流体(如蜂蜜)。
不可压缩意味着速度场不能有散度 \(\nabla \cdot \mathbf{u} = 0\) 。
求解方法:算子分裂(Operator Splitting)
忽略黏性项后:\[\frac{D \mathbf{u}}{D t} = -\frac{1}{\rho}\nabla p + \mathbf{g}, \quad \nabla \cdot \mathbf{u} = 0\]
可以将方程分解为三个部分:
\[\frac{D \mathbf{u}}{D t} = 0, \frac{D \mathbf{\alpha}}{D t} = 0 \quad \text{(advection)}\]
\[\frac{\partial \mathbf{u}}{\partial t} = g \quad \text{(external forces, optiona)}\]
\[\frac{\partial \mathbf{u}}{\partial t} = -\frac{1}{\rho}\nabla p \quad \nabla \cdot \mathbf{u} = 0 \quad \text{(projecton)}\]
\(\alpha\) :任何物理属性(温度,颜色,烟雾密度等)