关于机器学习课程
SJTU-SE3332-机器学习 课程笔记
1. 引言
定义:机器学习是一种人工智能技术,使机器能够在无需显式人工编程的情况下,通过从数据中自动发现潜在的统计规律(模型),并不断优化自身性能(优化),以实现特定的目标(如最小化损失函数)。
数据->训练/优化->统计模型->测试->指标
核心要素:
- 数据(经验)
- 模型(假设)
- 损失函数(目标)
- 优化算法(提升)
构建一个机器学习系统:
- 考虑数据可行性和规模
- 能获得多少数据?需要多少代价(时间、算力、人力成本)?
- 选择输入数据的合理表示形式
- 数据预处理,特征提取,等等。
- 选择合理的模型假设
- 选择合适的损失函数
- 选择或设计一个学习算法
流程:数据准备(数据收集、特征提取)→ 训练(训练、验证)→ 评估(预测、评估)
1.1. 机器学习分类
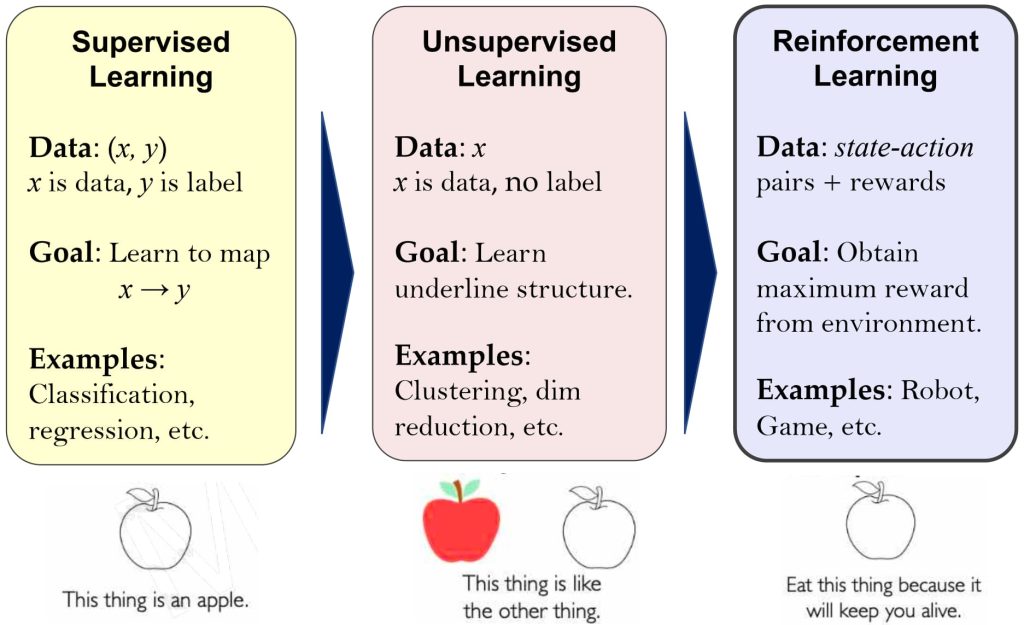
- 监督学习
- 数据:(x, y),x 表示数据, y 表示标签
- 学习目标:学习函数映射 x → y
- 典型任务: 分类、回归、目标检测、语义分割等
- 无监督学习
- 数据:x,x 表示数据,⽆标签
- 学习目标: 学习数据隐含或潜在的结构
- 典型任务: 聚类、降维和特征选择、概率密度估计、数据生成、异常检测等
- 强化学习
- 数据:通过自身(state)与环境交互(observation,reward 和 action)来学习
- 学习目标:学习状态(states)到动作(actions)的映射,以最大化长期奖励(reward)
- 典型任务: 蒙特卡洛强化学习等
1.2. 泛化能力
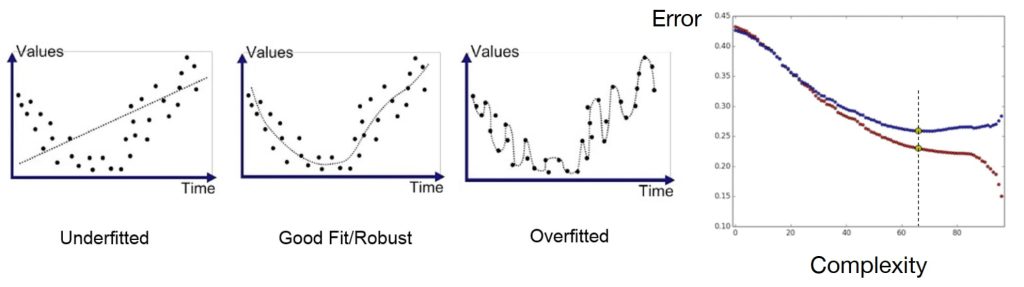
- 欠拟合 – 因模型不够复杂无法刻画真实规律,模型假设可能不成立。
- 过拟合 – 因模型过于复杂导致记住数据的细节(如随机噪声)而不是潜在的规律。
- 本质是模型的复杂度
常见的避免过拟合的方法:
- 增加训练数据(通过大量数据抑制模型记忆每个数据的细节)
- 正则化(惩罚模型复杂度)
- 数据划分 & 交叉验证(训练时用未知数据测试确保泛化能力)
- 早停
- 引入先验知识(如贝叶斯先验)
- 通常,设计好的损失函数评估预测模型在整个数据分布的表现,而非仅针对训练数据,有助于在模型结构的简单性与复杂性之间取得平衡。
1.2.1. 数据划分
- 模型拟合的是总体数据的分布而不仅仅是训练集的分布;
- 为了评估泛化误差,需要在训练的时候保留一部分未知数据;
- 数据划分(Hold-Out):训练集(e.g., 50%),验证集(e.g., 25%),测试集(e.g., 25%)。
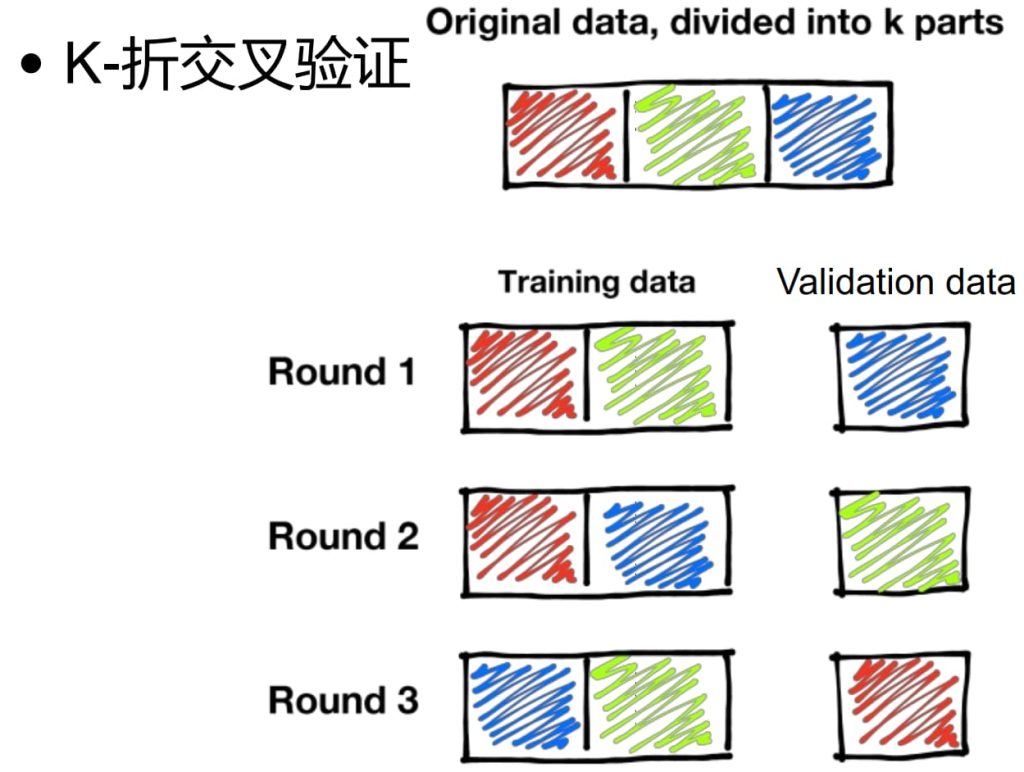
1.2.2. 交叉验证(Cross Validation)
- 充分利用有限数据(当数据规模较小),支持更多的训练集-测试集划分;
- 更能反映模型在未知数据上的表现;
- 需要更多计算资源和时间。
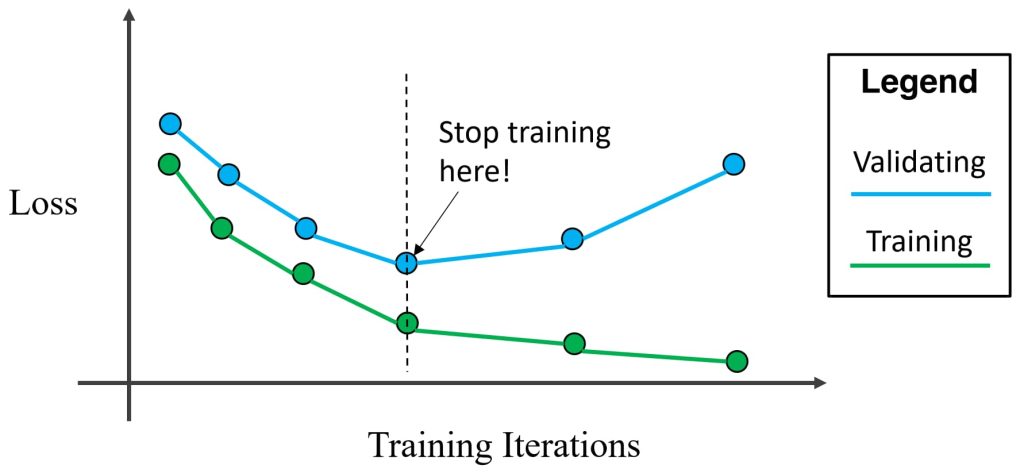
1.2.3. 早停(Early Stop)
- 在有过拟合迹象时及时停止训练。
1.2.4. 正则化(Regularization)
- 正则化的核心思想是在损失函数中引入对模型参数的惩罚项,通过限制参数的大小或稀疏性,防止模型过度拟合训练数据。
- e.g. \(L(W, \lambda_1, \lambda_2) = \|y – WX\|^2 + \lambda_2\|W\|_2^2 + \lambda_1\|W\|_1\)(其中:\(\|y – WX\|^2\)是均方误差损失(原始损失函数),\(\lambda_2\|W\|_2^2\)是 L2正则化项(权重衰减),\(\lambda_1\|W\|_1\)是 L1正则化项(稀疏约束),同时使用L1和L2正则化,称为弹性网络(Elastic Net))
- L2正则化(Ridge Regression)
- 稠密(参数接近但不为零)
- 约束参数的大小:强制所有参数 wi 趋向于较小的值(但不为零)。
- 防止过拟合:通过惩罚大权重,降低模型对训练数据中噪声的敏感度。
- 保持参数平滑:适合特征间相关性较强的场景(如线性回归 / 分类任务)。
- L1正则化(Lasso Regression)
- 稀疏(部分参数为零)
- 特征选择:通过将部分参数压缩为零,自动筛选重要特征。
- 增强稀疏性:适合高维数据(如特征数 >> 样本数)。
- 计算复杂度:需迭代优化(如坐标下降)。
2. 线性回归(Linear Regression)
2.1. 回归问题
- 原因:回归的核心目的是通过实验观测数据,揭示变量间的统计关系,回归数据变量的真实值。
- 预测:基于已知变量(特征)预测未知变量(目标)。
- 解释:量化自变量(X)对因变量(y)的影响程度。
- 去噪:从带有误差的观测数据中逼近真实规律。
- 关键思想是用数学函数拟合数据中的“趋势”,区分信号(规律)与噪声(随机波动)。
- 定义:回归是一种描述因变量(dependent variable)与一个或多个自变量(independent variables)之间关系的统计方法,其数学形式为:\(y = f(X) + ϵ\)。
- \(y\):因变量(需要预测的目标);\(X\):自变量(特征,可为一个或多个);\(f(X)\):回归模型(拟合的函数);\(ϵ\):随机误差(无法被模型解释的部分)。
- 核心任务:找到最优函数 \(f(X)\),使预测值 \(\hat{y} = f(X) + ϵ\)尽可能接近真实值 \(y\)。
- 常见类型:
- 线性回归:因变量与自变量呈线性关系,\(y=w_1x_1+w_2x_2+b\)
- 多项式回归:非线性关系(如曲线趋势),\(y=w_1x+w_2x^2+b\)
- 岭回归(L2正则化):高维数据或特征共线性,损失函数中加入 \(\lambda\|w\|_2^2\)
- Lasso回归(L1正则化):特征选择(稀疏解),损失函数中加入 \(\lambda\|w\|_1\)
2.2. 模型
使用线性函数(核心)回归:\(y=f(x)=\mathbf{w}^Tx+w_0\)
\(\underbrace{x_0, x_1, \dots, x_d}_{\text{输入}} \overset{w_0, w_1, \dots, w_d}{\longrightarrow} \underbrace{f(x) = \mathbf{w}^T x + w_0}_{\text{模型}} \rightarrow \underset{\text{预测值}}{y} \text{误差} \underset{\text{目标值}}{r}\)
- 训练过程:
- 根据数据误差,估算合适的参数 \(w\) 和 \(w_0\)
- 预测过程:
- 对于输入的新数据 \(x\),计算\(f(x) = \mathbf{w}^T x + w_0\),得到回归值\(y\)
2.3. 损失函数
- 对于任一输入样本 \(x\),模型输出预测值 \(y\). 令 \(r \in R\) 为该样本对应的目标值,则相应的平方误差定义为(可以避免正负值的区别):
- \(l(w, w_0 \mid x, r) = (r – y)^2\)
- 对于完整数据集 \(D = \{{(x^{(1)}, r^{(1)}), \ldots, (x^{(N)}, r^{(N)})}\}\),损失函数定义为均方误差(MSE):
- \(L(w, w_0 \mid D) = \frac{1}{2N} \sum_{\ell=1}^{N} \bigl(r^{(\ell)} – y^{(\ell)}\bigr)^2\)
- 除以 2 的目的是为了简化后续优化计算中的梯度公式推导,常数系数不会影响模型参数的优化方向。
2.4. 优化
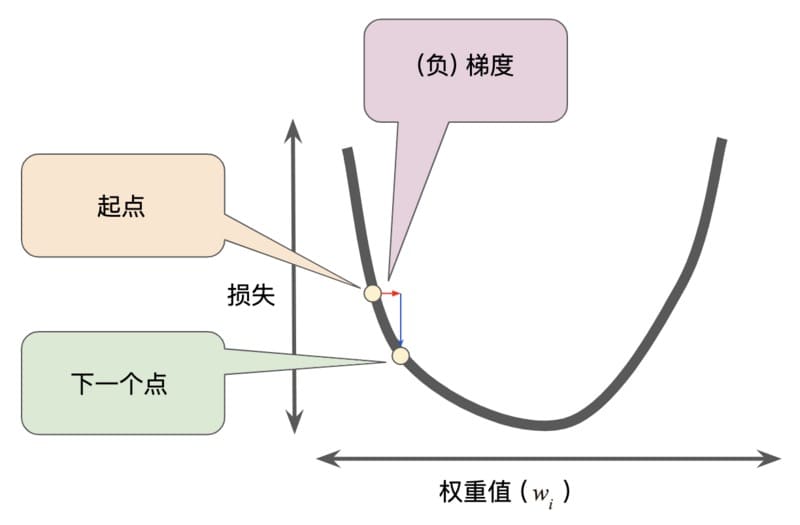
一般采用梯度下降法(Gradient Descend)优化损失函数:
- 优化目标:\(min_wL(w)\)
- 迭代步骤:\(w_{t+1}=w_t-\eta _t\frac{\partial L}{\partial w}\)

- 计算 \(\frac{\partial L}{\partial w}\):
- \(L(w, w_0 \mid D) = \frac{1}{2N} \sum_{\ell=1}^{N} \bigl(r^{(\ell)} – y^{(\ell)}\bigr)^2\)
- 对于任意 \(w_j(j=1,\dots,d)\):
- \(\frac{\partial L}{\partial w_j} = \frac{\partial L}{\partial y}\cdot\frac{\partial y}{\partial w_j} = -\frac{1}{N} \sum\limits_{\ell} \underbrace{\big(r^{(\ell)} – y^{(\ell)}\big) \frac{\partial y^{(\ell)}}{\partial w_j}}_{\text{Chain rule}} = -\frac{1}{N} \sum\limits_{\ell} \big(r^{(\ell)} – y^{(\ell)}\big) x_j^{(\ell)}\)
- 迭代规则:
- \(\mathbf{w}_{\text{new}} = \mathbf{w}_{\text{old}} + \frac{1}{N} \sum_{\ell=1}^N \big(r^{(\ell)} – y^{(\ell)}\big) x^{(\ell)}\)
2.5. 矩阵形式
令 \(X = \begin{bmatrix} \mathbf{x}^{(1)} \\ \mathbf{x}^{(2)} \\ \vdots \\ \mathbf{x}^{(N)} \end{bmatrix} = \begin{bmatrix} x_{0}^{(1)} & x_{1}^{(1)} & x_{2}^{(1)} & \cdots & x_{d}^{(1)} \\ x_{0}^{(2)} & x_{1}^{(2)} & x_{2}^{(2)} & \cdots & x_{d}^{(2)} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\ x_{0}^{(N)} & x_{1}^{(N)} & x_{2}^{(N)} & \cdots & x_{d}^{(N)} \end{bmatrix} \quad \mathbf{w} = \begin{bmatrix} w_{1} \\ w_{2} \\ \vdots \\ w_{d} \end{bmatrix} \quad \mathbf{r} = \begin{bmatrix} r^{(1)} \\ r^{(2)} \\ \vdots \\ r^{(N)} \end{bmatrix}\)
- 预测值:\(\mathbf{y} = X\mathbf{w} = \begin{bmatrix} \mathbf{x}^{(1)}\mathbf{w} \\ \mathbf{x}^{(2)}\mathbf{w} \\ \vdots \\ \mathbf{x}^{(N)}\mathbf{w} \end{bmatrix}\)
- 损失函数:\(L(\mathbf{w}) = \frac{1}{2}(\mathbf{r}-\mathbf{y})^{T}(\mathbf{r}-\mathbf{y}) = \frac{1}{2}(\mathbf{r}-X\mathbf{w})^{T}(\mathbf{r}-X\mathbf{w})\)
- 梯度:\(\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}} = -X^{T}(\mathbf{r}-X\mathbf{w})\)
- 最优参数:\(\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}} = 0 \Rightarrow X^{T}(\mathbf{r}-X\mathbf{w}) = 0 \Rightarrow X^{T}\mathbf{r} = X^{T}X\mathbf{w} \Rightarrow \mathbf{w}^{*} = (X^{T}X)^{-1}X^{T}\mathbf{r}\)
- 将最优参数\(w^*\)代入原始模型,得到预测值为\(y=X(X^TX)^{-1}X^Tr=\mathbf{H}r\)
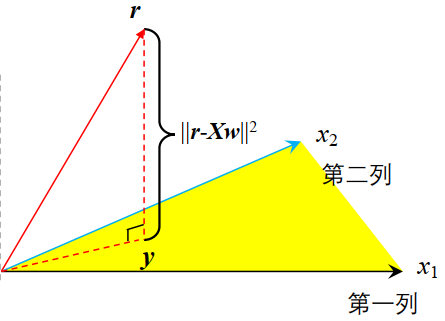
- 几何解释
- \(\mathbf{y}\) 是 \(X\) 的线性组合,因此是 \(X\) 列向量\([\mathbf{x}_1,\mathbf{x}_2,\dots,\mathbf{x}_d]\)构成的子空间上的一点 ;
- \(\mathbf{y}=\mathbf{Hr}\),说明\(\mathbf{H}\) 将 \(\mathbf{r}\) 投射到\(\mathbf{y}\);
- 需要 \(\mathbf{y}\) 与\(\mathbf{r}\) 距离最短,因此 \(\mathbf{H}\) 是向量 \(\mathbf{r}\) 在该子空间上距离最短的一个投影。
- 问题:\(X^TX\) 可能不可逆,当某些列向量线性相关时(例如 \(x_2 = 3x_1\)),矩阵 \(X^TX\) 是奇异的,因此无法直接计算 \(\mathbf{w}^* = (X^TX)^{-1}X^T\mathbf{r}\)。
- 解决方法:正则化 \(L(w) = \frac{1}{2}(\mathbf{r}-\mathbf{y})^T(\mathbf{r}-\mathbf{y}) = \frac{1}{2}(\mathbf{r}-X\mathbf{w})^T(\mathbf{r}-X\mathbf{w}) + \underline{\frac{\lambda}{2}\|\mathbf{w}\|_2^2}\)
- 新的梯度:\(\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}} = -X^T(\mathbf{r}-X\mathbf{w}) + \underline{\lambda \mathbf{w}}\)
- 新的最优解:\(\frac{\partial L(\mathbf{w})}{\partial \mathbf{w}} = 0 \Rightarrow -X^T(\mathbf{r}-X\mathbf{w}) + \underline{\lambda \mathbf{w}} = 0 \\ \Rightarrow X^T\mathbf{r} = (X^TX+\underline{\lambda I})\mathbf{w} \Rightarrow \mathbf{w}^* = (X^TX+\underline{\lambda I})^{-1}X^T\mathbf{r}\)
- 正则化相当于对模型进行数据增强(添加数据先验)。
3. 决策树(Decision Tree)
3.1. 回归 vs. 分类
- 回归(预测连续值标签):
- 对数据点在(d+1)维空间(d 是特征维度,+1 维是标签轴 y)中的分布进行建模。
- 分类(预测类别标签):
- 对 d 维空间中不同类别数据的分界边界进行建模,通过决策边界划分不同类别区域。
3.2. 模型
- 数据分布:非线性,可能非数值,但是沿着某些维度局部线性可分(组合一组不同的线性模型,每个模型覆盖输入空间中互不重叠的区域,递归划分为多个线性可分的子问题)。
- 基本思想:分而治之(划分数据属性,创建 if-then 规则)。
- 决策树:通过一系列决策规则对数据进行分类。
- 结构:
- 决策树包含三种类型的节点:
- 根节点(root node)
- 中间节点(Internal nodes)
- 叶子节点(Leaf nodes,terminal nodes)
- 每个叶子节点对应一个类别标签;
- 每个非叶子节点包含属性测试条件,用来根据属性不同特征划分数据。
- 决策树包含三种类型的节点:
3.3. 模型训练(构建决策树)
自顶向下分治学习
- 构造一个根节点,包含整个数据集;
- 选择一个最合适的属性;
- 根据选择属性的不同取值,将当前节点的样本划分成若干子集;
- 对每个划分后的子集创建一个孩子节点,并将子集的数据传给该孩子节点;
- 递归重复2~4直到满足停止条件.
关键问题
- 决策树将数据逐步分割成越来越小的子集。最理想的情况是叶节点对应的样本属于同一类别(节点的标签纯净)。
- 如何高效率地构建决策树:
- 选择每个属性 X 的时候,尽可能最大化标签 Y 的纯度。
- 如何选择属性以最大化标签的纯度:
- 选择X以最大化信息增益、Gini系数等(每⼀种指标对应⼀种决策树构造算法)。
训练算法:按照不同的属性划分原则,有以下常⻅算法:
| 名称 | 分裂标准 | 支持的任务 | 生成树结构 | 处理缺失值 | 剪枝策略 |
| ID3 | 信息增益(Information Gain),偏向选择取值较多的属性 | 分类 | 多叉树 | 不支持 | 无 |
| CART | 基尼指数(Gini Index),适用分类任务,也支持回归树(基于均方误差) | 分类、回归 | 二叉树 | 支持 | 预剪枝和后剪枝 |
| C4.5 | 信息增益率(Gain Ratio),解决了信息增益偏向取值较多属性的问题 | 分类 | 多叉树 | 支持 | 后剪枝 |
3.3.1. ID3 算法
通过评估样本的整体信息熵的降低程度来决定划分使用的属性,使信息增益(Information Gain)最大化。
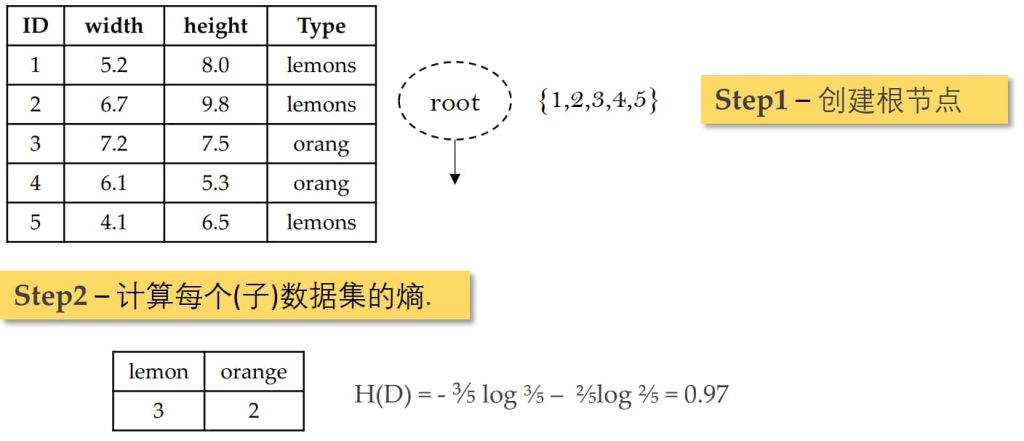
熵—刻画一个数据集合的不纯净度:
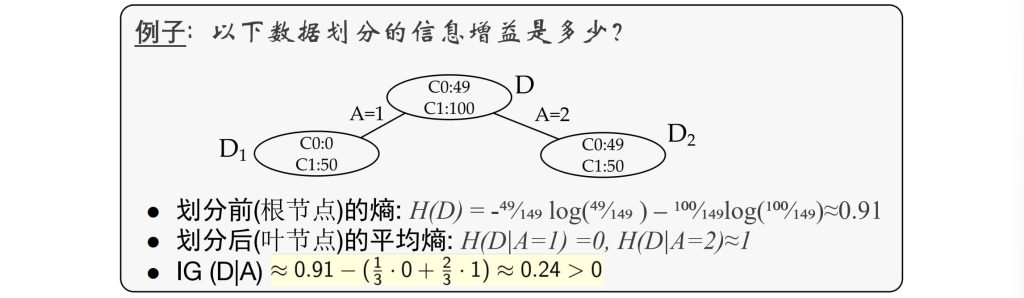
- \(H(D) = – \sum_{k=1}^{K} p_k \log p_k = – \sum_{k=1}^{K} \frac{|C_k|}{D} \log \frac{|C_k|}{D}\)
- \(|C_k|\):数据集 D 中 \(C_k\) 类的数量;
- \(H(D|A) = \sum_{i=1}^{n} \frac{|D_i|}{|D|} H(D_i) = -\sum_{i=1}^{n} \frac{|D_i|}{|D|} \left( \sum_{k=1}^{K} \frac{|D_{ik}|}{|D_i|} \log \frac{|D_{ik}|}{|D_i|} \right)\)
- \(H(D_i) = H(D|A=value_i)\)
- \(|D_i|\):数据集中属性 A 取第 i 个值的样本数量;
- \(|D_{ik}|\):在 \(D_i\) 中属于类别 \(C_k\) 的样本数量。
- \(Gain(D,A) = H(D) – H(D|A)\)
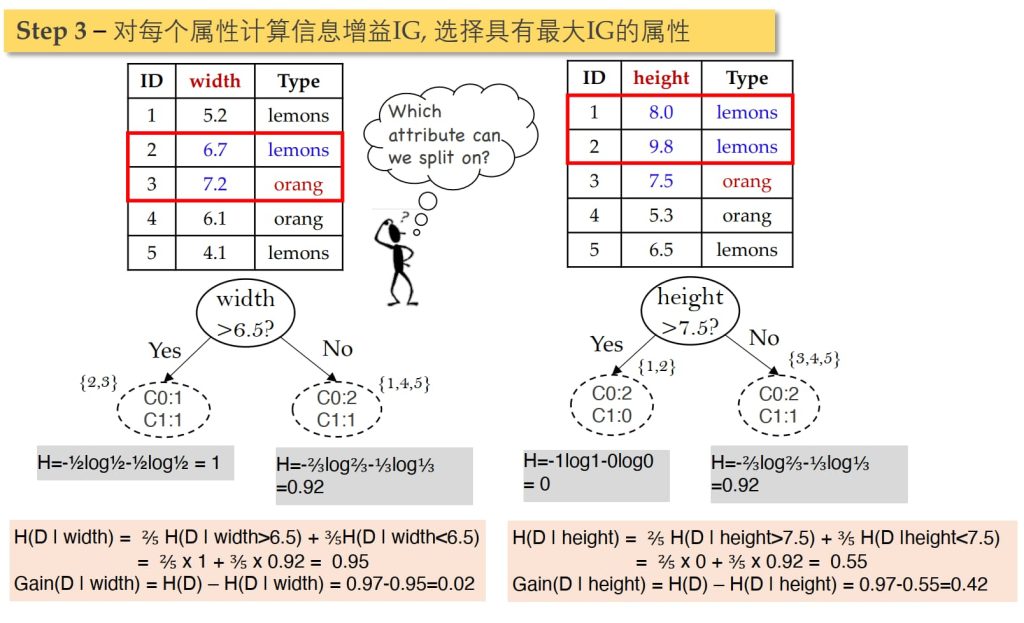
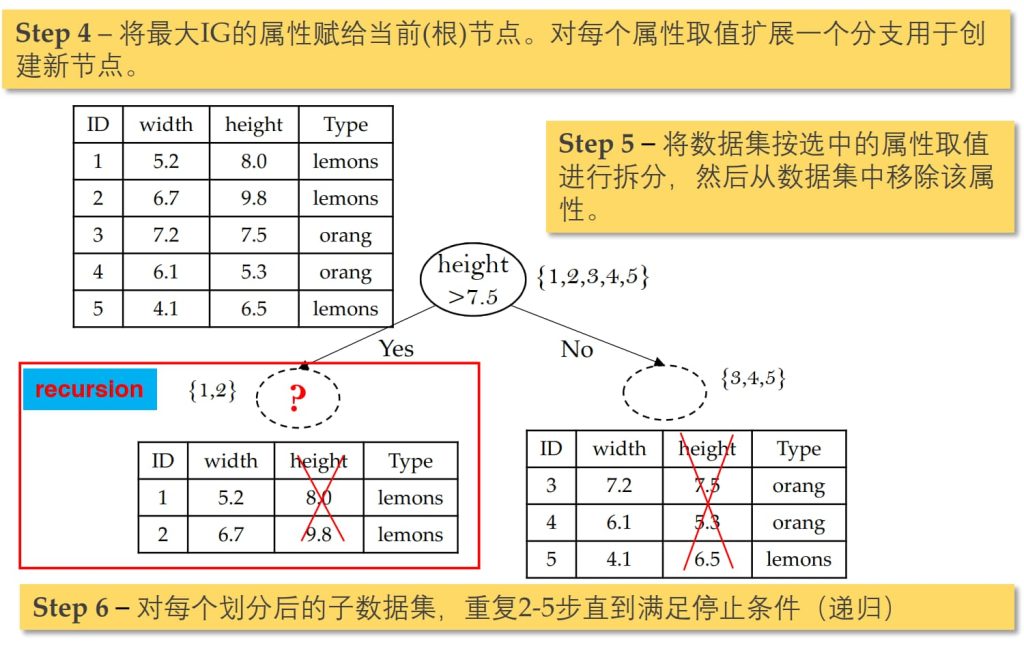
停止划分的条件:
- 纯度:叶子节点包含的样本均属于同一类
- 数据量过小:叶子节点包含的样本数小于一个阈值
- 没有属性可分(ID3):ID3对每个属性只划分一次
- 优点:
- 易理解, 可解释性, 便于可视化分析;
- 数据预处理要求低;
- 可以轻易处理非线性边界;
- 数据驱动,可以以任意精度拟合训练集。
- 缺点:
- 容易过拟合
3.3.2. 随机森林
- 将数据随机划分子集,各自构建决策树,将结果合并。
- 解决过拟合的一种有效方式。
算法过程:
- 从原始数据集中有放回地随机抽取 N 个样本,构成一个子训练集(每次抽样可能包含重复样本);
- 基于该子训练集构建决策树,其中每个节点的分裂规则如下:
- 随机属性选择:从所有特征中随机抽取 d 个候选属性;
- 节点分裂:根据选定属性(如基于信息增益)选择最佳分裂方式。
- 将步骤1~2重复执行 k 次,生成 k 棵不同的决策树;
- 汇总所有决策树的预测结果,通过多数投票法(分类任务)或平均法(回归任务)生成最终结果。
- 优点(用随机性换稳定性,用集成换精度):
- 通过双重随机性(数据自助采样 + 特征子集随机选择)降低过拟合风险,比单棵决策树更准确;
- 可以处理高维(feature很多)数据,并且不用做特征选择 (因为特征子集是随机选择的);
- 训练速度快(树与树独立生成,天然支持并行化);
- 可处理缺失值、不平衡数据(通过采样平衡误差)和特征交互(自动检测特征间关系);
- 提供特征重要性排序,同时保持集成模型的直观解释性(i.e.,在训练完后,能够给出哪些feature比较重要)。
4. 贝叶斯分类(Bayesian Classification)
4.1. 模型
- 数据分布:不能通过线性或递归方式分离,但具有明确的概率分布和依赖关系模式(如正态分布)。
- 基本思想:贝叶斯分类基于概率论的原理,通过将样本的不同维度表示为随机变量,建模这些变量之间的概率关系。核心在于计算样本的后验概率,基于后验概率最大化原则(MAP,Maximum A Posteriori),选择最有可能的类别作为预测结果。
- 此外,若假设特征之间条件独立(即朴素贝叶斯假设),模型的计算复杂度大幅降低,但同时可能会牺牲一定的准确性。
贝叶斯公式分解计算后验概率:\(P(C_i|x)=\frac{p(x|C_i)P(C_i)}{p(x)}, \ i=1,2,\dots,N\)
- \(C_i\) 是第 i 个类别(共N个),\(x\) 数据特征向量;
- \(P(C_i)\) 先验概率,在未观测数据时,类别 \(P(C_i)\) 的初始概率(可通过训练集频率估计);
- \(p(x|C_i)\) 似然概率,在类别 \(C_i\) 成立的条件下,观测到数据 x 的概率;
- \(p(x)\) 证据概率,是所有类别下生成特征 x 的总概率,用于归一化;
- \(p(x) = \sum_{i=1}^N P(C_i)p(x|C_i)\)
- \(p(C_i|x)\) 后验概率,观察到数据 x 后,样本属于类别\(C_i\)的概率。
基于 MAP,\(C_{MAP} = \underset{i}{argmax} P(C_i|x) = \underset{i}{argmax} p(x|C_i)P(C_i)\)(p(x) 相同)
对于高维数据,不同特征看作多个随机变量,\(C_{MAP} = \underset{i}{argmax} p(x_1,x_2,\dots,x_d|C_i)P(C_i)\)(d为数据维度数)
- \(P(C_i) = \frac{\text{count}(C_i)}{N}\),N为总训练样本数,\(\text{count}(C_i)\)为属于第 i 个类别的训练样本数;
- \(p(x_1,x_2,\dots,x_d|C_i)\),通过联合概率表获得,但对于高维数据非常庞大。
4.2. 朴素贝叶斯假设(Naïve Bayes Independent Assumption)
条件独立性(Conditional Independence):假设在给定类别 C 的条件下,输入特征 \(x_j\) 之间是相互独立的。
- \(p(x_1,x_2,\dots,x_d|C) = P(x_1|C) \cdot P(x_2|x_1,C) \dots P(x_d|x_1,\dots,x_{d-1},C) \approx P(x_1|C) \cdot P(x_2|C) \dots P(x_d|C) \)
- \(C_{NB} = \underset{i}{argmax} \ p(x_1,x_2,\dots,x_d|C_i)P(C_i) = \underset{i}{argmax} \ P(C_i) \prod_{j=1}^{d}p(x_j|C_i) \)
- \(p(x_j|C_i) = \frac{\text{count}(x_j|C_i)}{count(C_i)} = \frac{\text{count}(x_j|C_i)}{\sum_{j=1}^{d}\text{count}(x_j,C_i)}\)
- 其中 \(\text{count}(x_j|C_i)\) 是同时属于 \(x_j, C_i\) 特征的样本。
零概率问题(Zero Counts)
- 在贝叶斯分类中,当某类别 \(C_i\) 的训练样本中没有出现某属性值 \(x_j\) 时,条件概率 \(\hat{P}(x_j|C_i) = 0\)。
- 根据贝叶斯公式,类别 \(C_i\) 的后验概率会受到零概率的影响,导致 \(P(C_i) \prod_{j=1}^{d}p(x_j|C_i) = 0\)。
- 解决方法:拉普拉斯平滑(Laplace Smoothing):
- 为每个属性值增加一个虚拟计数(virtual count),以避免条件概率为零的问题。
- 更新公式:\(\hat{P}(x_i \mid C_i) = \frac{\text{count}(x_j, C_i) + 1}{\sum_{j=1}^{d} \text{count}(x_j, C_i) + |\mathcal{X}|}\)
- 分子:类别 \(C_i\) 中属性值 \(x_j\) 的频数加上 1。
- 分母:类别 \(C_i\) 的所有属性值频数之和,加上属性值的总数 \(|\mathcal{X}|\)(即词汇表大小或取值范围)。
- 确保每个条件概率非零,避免分类中某些类别被完全排除;增加模型的鲁棒性,特别是在小样本或稀疏数据中。
4.3. 应用和优缺点
- 应用场景
- 文本分类:特别适用于多分类问题,由于独立性假设,效果优于许多其他算法。
- 实时预测:NB一种即刻学习(eager learning)的分类器,训练和预测速度非常快。
- 多分类预测:可以预测目标变量属于多个类别的概率,适合多分类场景。
- 优点:
- 快速:训练阶段:仅需对训练集进行一次遍历;预测阶段:计算量小,预测速度快。
- 表现竞争力:在特征独立性假设成立的情况下,表现优于许多复杂算法;在多分类预测中效果尤为显著。
- 易于更新:新增或删除训练样本时,模型更新简单且易于维护。
- 缺点:
- 条件独立性假设
- 假设特征之间相互独立,这在实际应用中经常被违背。
- 即使假设被违背,NB 在许多场景下仍能意外地取得不错的效果。
- 不需要后验概率完全正确,只需保证最大化的类别预测正确即可。
- 欠拟合(Underfitting)
- NB 模型复杂度低,难以捕获数据的深层次模式。
- 可以通过更复杂的贝叶斯网络(如信念网络)放宽独立性假设来解决。
- 条件独立性假设
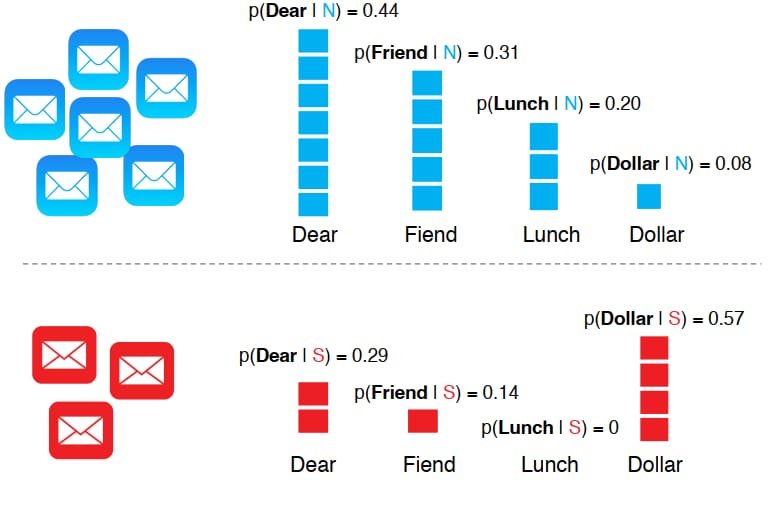
4.4. 朴素贝叶斯在文本分类的应用
- 输入:
- 训练数据集:共 m 个手动标注的文档,表示为 \((d_1,c_1),…,(d_m,c_m)\);其中,每个文档 \(d_i\) 包含单词 \(\{w_1, w_2, \dots, w_{|d|}\}\),\(c_i \in C\) 是文档对应的类别标签,类别集合为 \(C = \{c_1, \dots, c_{|C|}\}\) 。
- 训练:
- 提取词汇表:从训练语料中提取出词汇表 Vocab。
- 计算先验概率 \(P(c_j)\):
- 对于每个类别 \(c_j \in C\):\(P(c_j) = \frac{|\text{docs}_j|}{\text{total number of documents}}\) ;其中 \(docs_j\) 是类别为 \(c_j\) 的所有文档。
- 计算条件概率 \(P(w_k \mid c_j)\):
- 将 \(docs_j\) 中所有文档合并为一个文档 \(text_j\) 。
- 对于词汇表中每个单词 \(w_k\):\(P(w_k \mid c_j) = \frac{n_k + \alpha}{n + \alpha |\text{Vocab}|}\)。
- 其中,\(n_k\):单词 \(w_k\) 在 \(\text{text}_j\) 中的出现次数;n:\(\text{text}_j\) 中所有单词的总次数;\(\alpha\):平滑系数(如拉普拉斯平滑,通常为 1)。
- 测试:
- 对于一个新文档 \(d = \{w_1, w_2, \dots, w_{|d|}\}\):
- 对于每一个类别 \(c_i \in C\),计算分数:\(\text{score}(c) = P(c) \cdot P(w_1 \mid c) \cdot P(w_2 \mid c) \cdots P(w_{|d|} \mid c)\)。
- 输出具有最高分数的类别 c。
- 对于一个新文档 \(d = \{w_1, w_2, \dots, w_{|d|}\}\):

5. 最近邻(K-Nearest Neighbors,KNN)
核心原则:基于邻近样本的多数表决,一个样本的类别由其最近的 k 个邻居(训练数据)的多数类别决定,直接通过存储训练数据(”惰性学习”)和实时距离计算进行分类/回归(无需显式训练模型)。
5.1. 距离度量、归一化与相似度
- 距离度量
- 欧氏距离(Euclidean Distance,L2 范数):\(D(x,y) = \sqrt{\sum_{i=1}^n(x_i-y_i)^2}\),(在高维和类别型数据中效果差)。
- 曼哈顿距离(Manhattan Distance,L1 范数):\(D(x,y) = \sqrt{\sum_{i=1}^n|x_i-y_i|}\)。
- 闵氏距离(Minkowski Distance):\(D(x,y) = \big( {\sum_{i=1}^n(x_i-y_i)^p} \big) ^\frac{1}{p}\)
- 归一化(消除特征之间的量纲和数值范围差异,确保所有特征对距离的贡献相对公平):
- Z-score标准化:\(x_{\text{norm}} = \frac{x – \mu}{\sigma}\),将特征缩放到均值为0、标准差为1的分布。
- Min-Max归一化:\(x_{\text{norm}} = \frac{x – x_{\text{min}}}{x_{\text{max}} – x_{\text{min}}}\),将特征缩放到 [0, 1] 或 [-1, 1] 区间。
- 相似性(Similarity)
- 衡量两个数据对象相似程度的数值指标。
- 余弦相似度(Cosine Similarity)
- \(\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \times \|\mathbf{b}\|} = \frac{\sum_{i=1}^n a_i b_i}{\sqrt{\sum_{i=1}^n a_i^2} \times \sqrt{\sum_{i=1}^n b_i^2}} \quad \cos(\mathbf{d}_1, \mathbf{d}_2) = \begin{cases} 1: \text{方向完全相同} \\ 0: \text{正交(垂直)} \\ -1: \text{方向完全相反} \end{cases}\)
5.2. 算法
- 确定参数 K 的数值;
- 选取待分类测试样本并计算其与所有训练样本的距离;
- 对距离排序并选取 K 个最近邻样本;
- 根据 K 个邻居的多数投票结果确定测试样本类别。
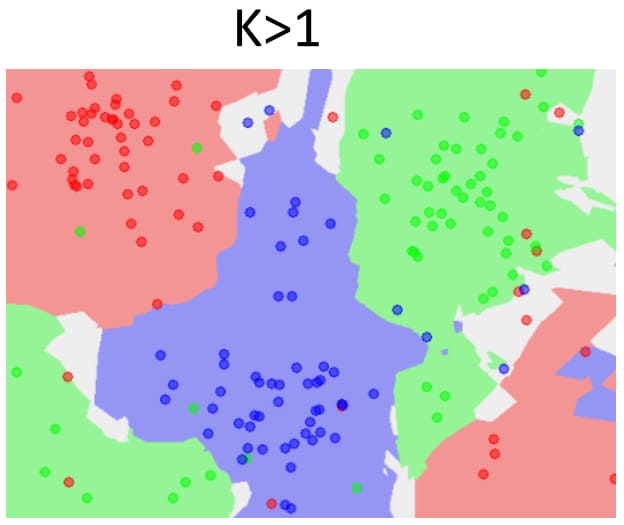
5.3. 参数 K 的选择与 KNN 的决策面(Decision Boundary)
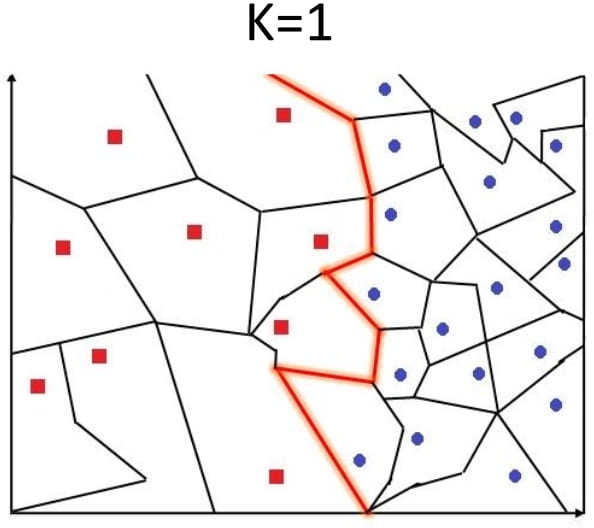
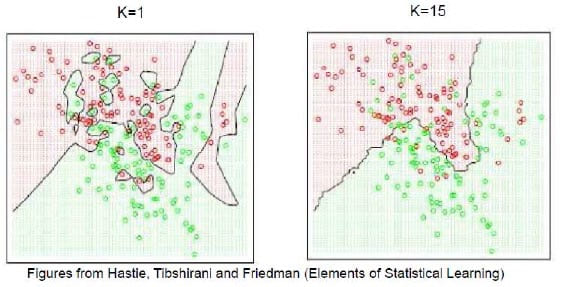
- Voronoi Tessellation(维诺图,沃罗诺伊分割)
- 将空间划分为离给定点最近的区域。
- 边界:与两个不同训练样本距离相同的点。
- 决策边界:分割不同类别的边界
- 参数 K 的影响:
- K值过小:效率提高,但容易受噪声影响。
- K值较大:效果较好,会产生更平滑的边界效果,但过大的K可能包含其他类别的多数点,导致分类结果过度平滑。
- 当K=N时,总是预测多数类。
5.4. 优缺点
- 优点:易于理解、解释和实现,无需训练过程(惰性学习)可动态新增数据,不影响模型准确性;
- 缺点:大数据集下性能差(距离计算计算成本高),对维数灾难高度敏感(高维数据失效),存储需求大(需保留全部训练数据),必须进行数据归一化(否则量纲影响结果)。
6. 逻辑回归(Logistics Regression)
6.1. 设想
思想:可以不需要知道数据的结构(不纯度(Impurity)、密度(Density)、距离),而直接预测决策面。
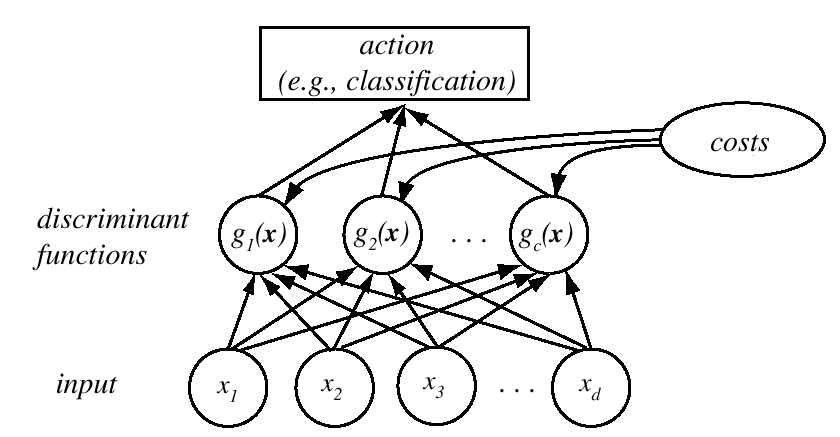
- 分类作为判别过程:
- 假设一个分类器有 c 个类;
- 定义 c 个判别函数 \(g_i(x)\);
- 决策规则:将 x 分配给类别 \(C_j\),如果 \(g_j(x)>g_i(x)\),对于所有 \(i \ne j\)
- 判别函数:
- 定义:用于用于表征数据属于某类别的程度,依赖于一组参数 \(\theta_i\), \(g_i(x \mid \theta_i)\)。
- 功能:直接且同时对类别间的决策边界建模,而不是估计类别的概率分布。
- 优势:直接确定类别边界(即判别函数)通常比估计类别概率分布更简单和高效。
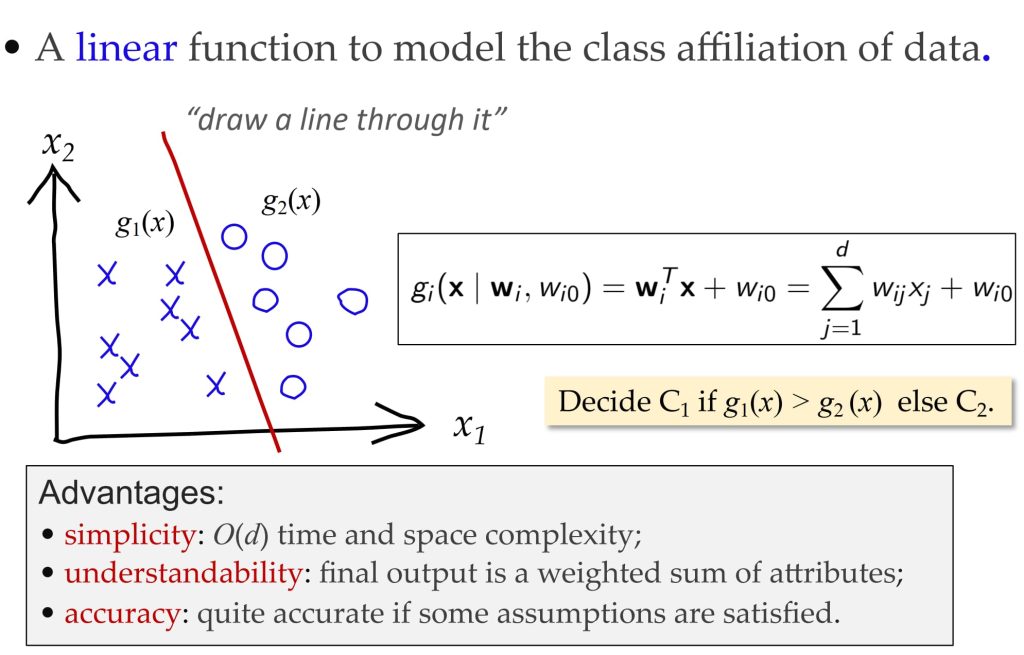

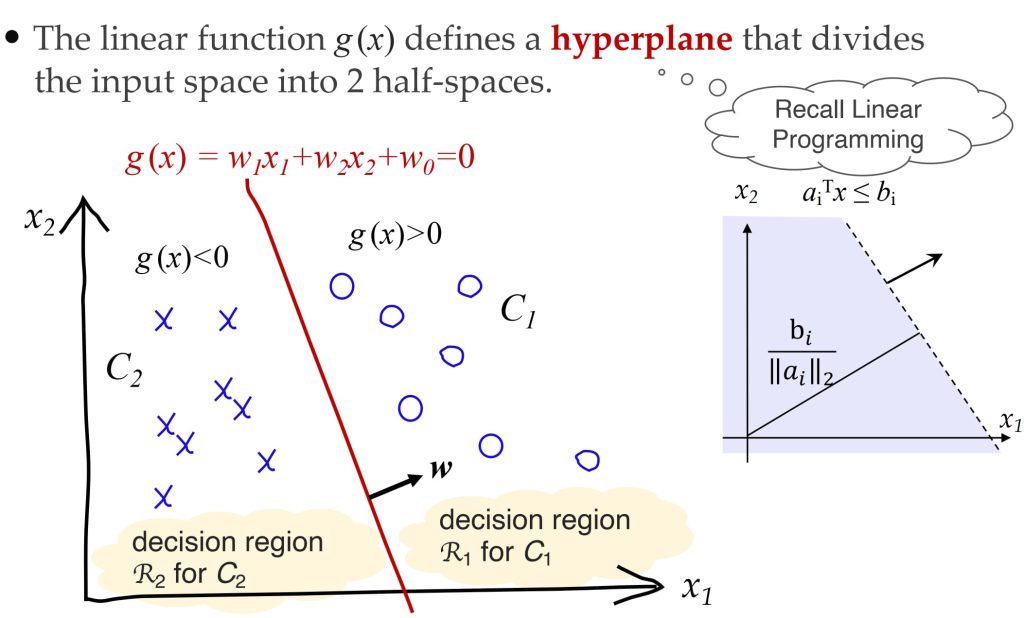
6.2. 感知机(Perceptron)
最开始,朴素线性分类器(naïve linear classifier):
\(\underbrace{x_0, x_1, \dots, x_d}_{\text{输入}} \overset{w_0, w_1, \dots, w_d}{\longrightarrow} \underbrace{g(x) = \mathbf{w}^T x + w_0}_{\text{分类器}} \rightarrow \underset{\text{预测值}}{g(x)>0?} \text{误差} \underset{\text{目标值}}{r}\)
- 训练:
- 从数据中预测参数 \(\mathbf{w},w_0\) 。
- 预测:
- 给定一个新 x,计算 g(x),选择 \(C_1 \ \text{if} \ g(x) > 0 \ \text{otherwise} \ C_2\) 。
- 感知机基于新点落在超平面的哪一侧来进行分类。
训练方法:
- 令 x 表示输入数据,\(r \in \{1, -1\}\) 表示目标类别的标签(即 g(x) 的符号)。
- 输入:数据集 \(D = \{(x^{(1)}, r^{(1)}), (x^{(2)}, r^{(2)}), \dots, (x^{(N)}, r^{(N)})\}\)
- 对于数据集中每个训练样本 \((x^{(\ell)}, r^{(\ell)}) \in D\):
- 检查分类错误:如果 \(r^{(\ell)} g_i(x^{(\ell)}) \leq 0\),则发生错误分类。
- 更新权重: \(w \leftarrow w + \eta \ r^{(\ell)} x^{(\ell)}\) 其中,\(\eta\) 为学习率。此步骤通过调整超平面(由 \(w\) 定义)向被错误分类的数据点移动。
- 检查分类错误:如果 \(r^{(\ell)} g_i(x^{(\ell)}) \leq 0\),则发生错误分类。
- 不断迭代上述过程,直到整个训练集被正确分类为止。
感知机的限制:
- 由于取值仅有 -1 和 1,对于优化来说非常难(无法刻画数据的偏离程度)。
- 解决方案:带有不确定性的线性分类
- 如何计算选择 \(C_1\) 或 \(C_2\) 的后验概率?
- 定义:\(P(C_1 \mid x) = y\),\(P(C_2 \mid x) = 1 – y\)
- 分类规则:\(\text{Choose} \ \begin{cases} C_1 \ \text{if} \ y > 0.5 \\ C_2 \ \text{otherwise} \end{cases}\)
- 等价规则:使用 y 的 概率比 (odds) 和 对数概率比 (logit function) 进行分类:
- 概率比:\(\frac{P(C_1 \mid x)}{P(C_2 \mid x)} = \frac{y}{1 – y}\)
- 对数概率比: \(\text{log odds} = \log\left(\frac{y}{1 – y}\right)\)

6.3. 逻辑回归
Sigmoid 函数:
- \( \log \frac{y}{1 – y} = \mathbf{w}^T\mathbf{x} + w_0 \Rightarrow y = \text{sigmoid}(\mathbf{w}^T\mathbf{x} + w_0) = \frac{1}{1 + \exp [-(\mathbf{w}^T\mathbf{x}) + w_0]}\)
- \(y = sigmoid(x) \ y’ = y(1-y)\)
Sigmoid 函数是 logit 函数的反函数,可直接计算后验类概率 \(P(C_1|x)\),Sigmoid 作为优化过程中的平滑函数。
基于 Sigmoid 函数设计逻辑回归:
使用逻辑函数估计决策边界的分类器:
\(\underbrace{x_0, x_1, \dots, x_d}_{\text{输入}} \overset{w_0, w_1, \dots, w_d}{\longrightarrow} \underbrace{y = \text{sigmoid}(\mathbf{w}^T \mathbf{x} + w_0)}_{\text{分类器}} \rightarrow \underset{\text{预测值}}{\hat{y}} \text{loss}(\hat{y},r) \underset{\text{目标值}}{r}\)
- 训练:
- 从数据中预测参数 \(\mathbf{w},w_0\) 。
- 预测:
- 给定一个新 x,计算 \(y = \text{sigmoid}(\mathbf{w}^T \mathbf{x} + w_0)\),选择 \(C_1 \ \text{if} \ y > 0.5 \ \text{otherwise} \ C_2\)(y 可以被认为是后验概率)。
损失函数:
- 对于给定 x,预测得到 y 值,定义 \(r \in \{0,1\}\) 为真实类的标签 \(r=1: x \in C_1,r=0: x \in C_2\):
- 如果 r = 1:目标是最大化 \(\log p(C_1 \mid x) = \log y, \text{损失为} – \log y\)
- 如果 r = 0:目标是最大化 \(\log p(C_2 \mid x) = \log (1 – y), \text{损失为} – \log (1 – y)\)
- 可以写为 交叉熵损失(cross-entropy loss):
- \(\text{CE}(p,q) = E_{x \sim p(x)}\{\log \frac{1}{q(x)}\} = – \sum\limits_{x \in X}p(x) \log_2 q(x)\)
- \( \ell (\mathbf{w},w_0 \mid x,r) = \underbrace{-r \log y}_{\text{nonzero only if
} r=1} \underbrace{-(1-r) \log (1-y)}_{\text{nonzero only if
} r=0}\)
- 等价于最大化似然(likelihood)
- \(r \mid x \sim \text{Bernoulli}(y)\)
- \(p(r \mid x) = y^r(1-y)^{(1-r)}=\begin{cases} y \quad \text{if} \ r = 1 \\ 1-y \quad \text{if} \ r = 0 \end{cases}\)
训练:
- 给定数据集 \(D = \{(x^{(1)}, r^{(1)}), \dots, (x^{(N)}, r^{(N)})\}\);
- 通过梯度下降(gradient descend)最小化损失函数;
- Goal:\(min_wL(\mathbf{w})\)
- Iteration:\(\mathbf{w}_{t+1} = \mathbf{w}_t – \eta_t \frac{\partial L}{\partial w}\)
梯度下降的优化过程:

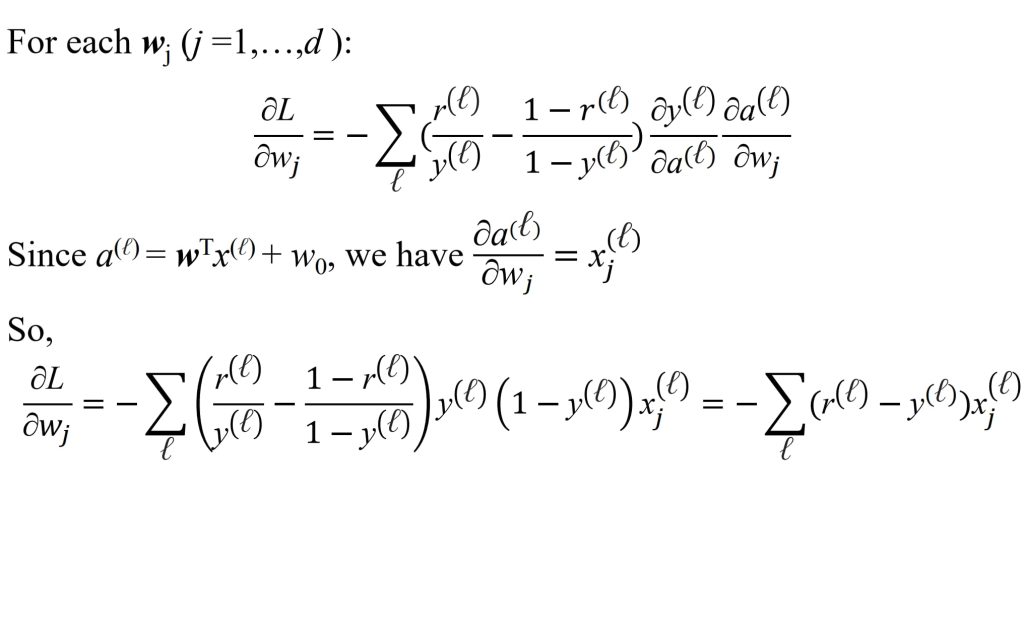

6.4. 多分类问题与 Softmax 回归
- Softmax 函数定义为:\(y_i = \text{softmax}(a_1, \dots, a_K)i = \frac{e^{a_i}}{\sum{j=1}^K e^{a_j}}\)
- 其中,输入 \(a_i = W_i x + w_{i0}\) 被称为 logits,\(W_i,w_{i0}\) 是可训练的参数。
- 功能:将 logits(分数)转换为一个概率分布。
- \(\text{if} \ a_k \gg a_j, \forall j \ne k, \text{then} \ p(C_k \mid \mathbf{x}) \approx 1, p(C_j \mid \mathbf{x}) \approx 0 \)
- 如果某个 \(a_k\) 明显大于其他值,Softmax 函数对 \((a_1, \dots, a_K)\) 的作用是 argmax 的平滑近似,因此它实际上更像 soft-argmax。
- max:因为它会放大最大 \(\text{logit} a_i\) 的概率。
- soft:因为它仍然会为较小的 \(a_j\) 分配一定的概率。
- 优势:Softmax 函数的行为类似于取最大值(max),但它具有可微性,因此更适合用于优化问题。
使用 Softmax 函数估计决策边界的分类器:
\(\underbrace{x_0, x_1, \dots, x_d}_{\text{输入}} \overset{w_0, w_1, \dots, w_d}{\longrightarrow} \underbrace{y = \text{softmax}(\mathbf{w}_i^T \mathbf{x} + w_{i0})}_{\text{分类器}} \rightarrow \underset{\text{预测值}}{\hat{y}_1, \dots, \hat{y}_K} \text{loss}(\hat{y},r) \underset{\text{目标值}}{r_1, \dots, r_K}\)
- 训练:
- 从数据中预测参数 \(\mathbf{w}_i,w_{i0} (i=1:K)\) 。
- 预测:
- 给定一个新 x,计算 \(y = \text{softmax}(\mathbf{w}_i^T \mathbf{x} + w_{i0})\),选择 \(C_1 \ \text{if} \ y_i = max\{y_{1:K}\}\)(y 可以被认为是后验概率)。
损失函数:
- 对于给定 x,模型输出一个类别概率向量 \(y = (y_1, \dots, y_K)\),目标类别的标签是一个 one-hot 向量 \(r = (r_1, \dots, r_K)\),(\(r_i = 1: x \in C_i,r_i = 0: x \notin C_i\))
- 如果 \(r_1 = 1\),我们希望最大化 \(\log p(C_1 \mid x) = \log y_1, \text{损失为} -\log y_1\)。
- 以此类推
- 可以写为 交叉熵损失(cross-entropy loss):
- \(L_{CE}= -\sum_{i=1}^K r_i \log y_i = -\mathbf{r}^T(\log \mathbf{y})\)
- 其中对数操作逐元素(elementwise)应用于 \(y_i\)。
训练:
- 给定数据集 \(D = \{(x^{(1)}, r^{(1)}), \dots, (x^{(N)}, r^{(N)})\}\);
- 通过梯度下降(gradient descend)最小化损失函数;
- Goal:\(min_wL(\mathbf{w})\)
- Iteration:\(\mathbf{w}_{t+1} = \mathbf{w}_t – \eta_t \frac{\partial L}{\partial w}\)
梯度下降的优化过程:
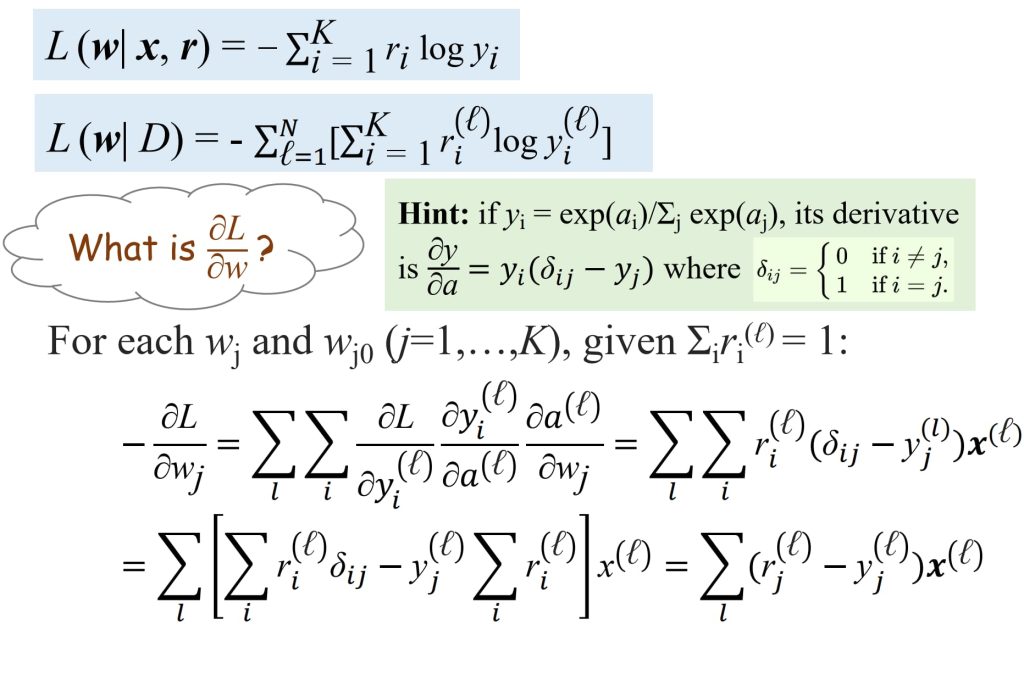

6.5. 优缺点
- 优点:
- 简单高效,计算复杂度低,训练和预测速度快,适合大规模数据集
- 可解释性强,权重参数直接反映特征重要性
- 线性可分数据下能收敛到最优解
- 缺点:
- 对于线性不可分问题:无法处理非线性边界(如异或问题),依赖人工特征工程(如多项式特征扩展)
- 对于多解问题:即使数据线性可分,也可能存在多个解(决策边界不唯一)
- 对噪声敏感,异常点可能显著影响决策边界
7. 支持向量机(Support Vector Machine)
7.1. 设想
- 逻辑回归得到的超平面可以有很多个,追求效果好应该找到能够最大化两个类之间的边距(margin)的决策边界。


每一个点满足左图的需求,即等价为 \(y^{(\ell)} (w^T x^{(\ell)} + w_0) \ge 1\)
7.2. 模型
- SVM 的目标是求解以下带约束的优化问题:
- minimize \(\frac{1}{2} \|\mathbf{w}\|^2\)
- subject to \(y^{(\ell)} (\mathbf{w}^T x^{(\ell)} + w_0) \ge 1, \ell=1,\dots,N\)
- 问题性质:
- 二次规划(QP)问题:目标函数为二次型,约束为线性,属于凸优化问题,存在全局最优解。
- 计算复杂度:主要取决于输入特征的维度 dd,维度越高计算成本越大。
与感知机模型相同
使用逻辑函数估计决策边界的分类器:
\(\underbrace{x_0, x_1, \dots, x_d}_{\text{输入}} \overset{w_0, w_1, \dots, w_d}{\longrightarrow} \underbrace{g(x) = \mathbf{w}^T x + w_0}_{\text{分类器}} \rightarrow \underset{\text{预测值}}{g(x)} \text{误差} \underset{\text{目标值}}{y}\)
- 训练:
- 从数据中预测参数 \(\mathbf{w},w_0\) 。
- 预测:
- 给定一个新 x,计算 g(x),选择 \(C_1 \ \text{if} \ g(x) > 1 \ \text{or} \ C_2 \ \text{if} \ g(x) < -1\) 。
损失函数:
- 对于给定 x,模型输出一个分数 g(x),令 \(y \in \{-1, +1\}\) 为真实类别的标签,(\(y = +1: x \in C_1,y = -1: x \in C_2\))
- 如果 \(y(w^T x + w_0) < 1\):我们希望最大化 \(y(w^T x + w_0)\) 直到达到 1,损失为 \(1 – y(w^T x + w_0)\)。
- 如果 \(y(w^T x + w_0) \geq 1\):为离群点(outlier points),无需优化,损失为 0。
- 可以简洁地写为 Hinge Loss:
- \(\ell(w, w_0 \mid x, y) = \max(0, 1 – y(w^T x + w_0))\)
- 给定数据集 \(D = \{(x^{(1)}, r^{(1)}), \dots, (x^{(N)}, r^{(N)})\}\),数据集上的损失函数定义为:
- \(L(w, w_0 \mid D) = \frac{1}{N} \sum_{\ell=1}^N \max(0, 1 – y^{(\ell)}(w^T x^{(\ell)} + w_0)) + \frac{\lambda}{2} ||w||^2\)
梯度下降的优化过程:


8. 多层感知机(Multi-layer Perceptrons)
8.1. 设想
- 人工神经网络(Artificial Neural Networks, ANN)模仿了人类大脑的某些特性,尤其在计算层面的仿生机制。
- 感知机可以被用作回归和分类,学习布尔函数等价于一个二分类问题,但有局限性:无法学习非线性可分数据(如 XOR 问题)。
- 引入神奇的隐藏层(Hidden Layers):
- 添加隐藏层(内部表示)使得模型能够学习一种不受线性可分性约束的映射;
- 多层感知机能够通过组合隐藏层的线性单元来学习复杂的决策边界,允许模型解决更复杂的分类问题。
- e.g. \(x_1 \ \text{XOR} \ x_2 = ( x_1 \ \text{AND} \ \sim x_2) \text{or} (\sim x_1 \ \text{AND} \ x_2)\)
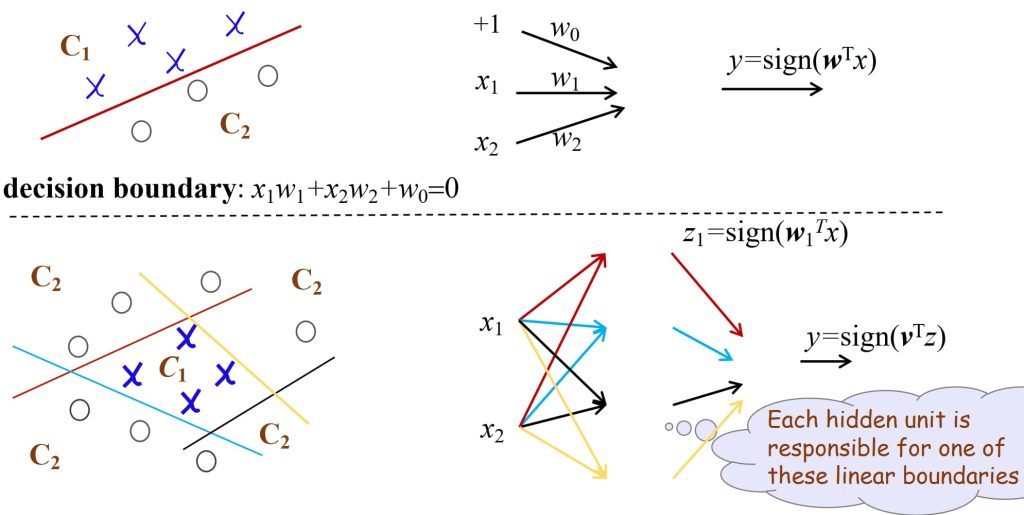
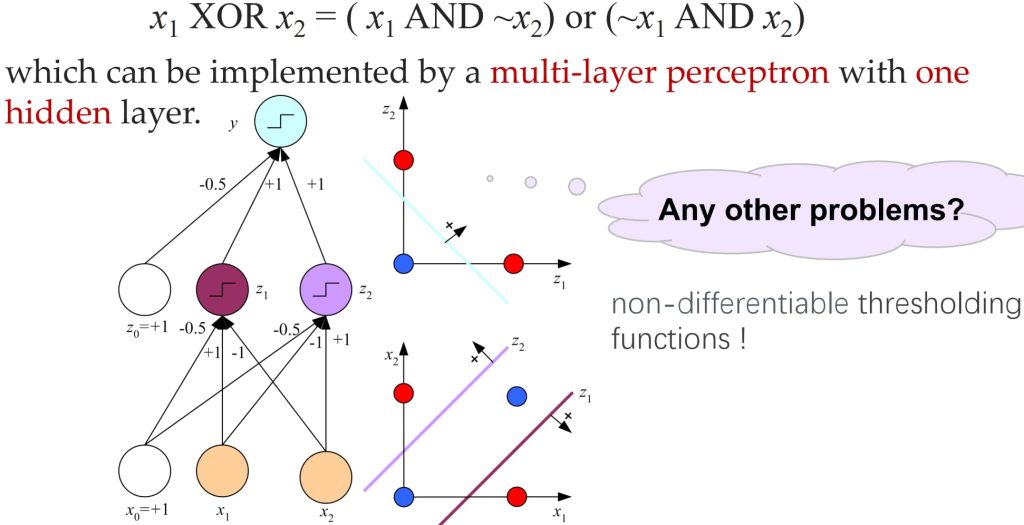
激活函数(Activation Functions):一般来说,可以使用许多其他连续、可微分的阈值函数(称为激活函数)来引入非线性特性到感知机中。
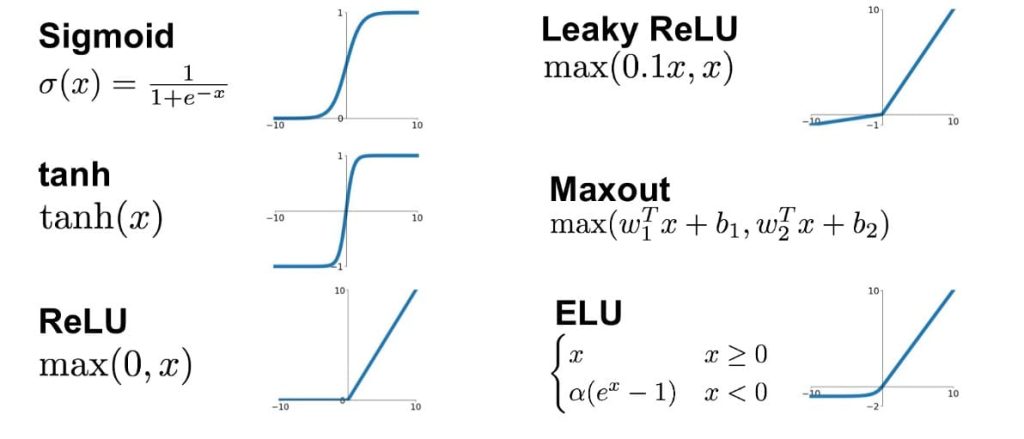
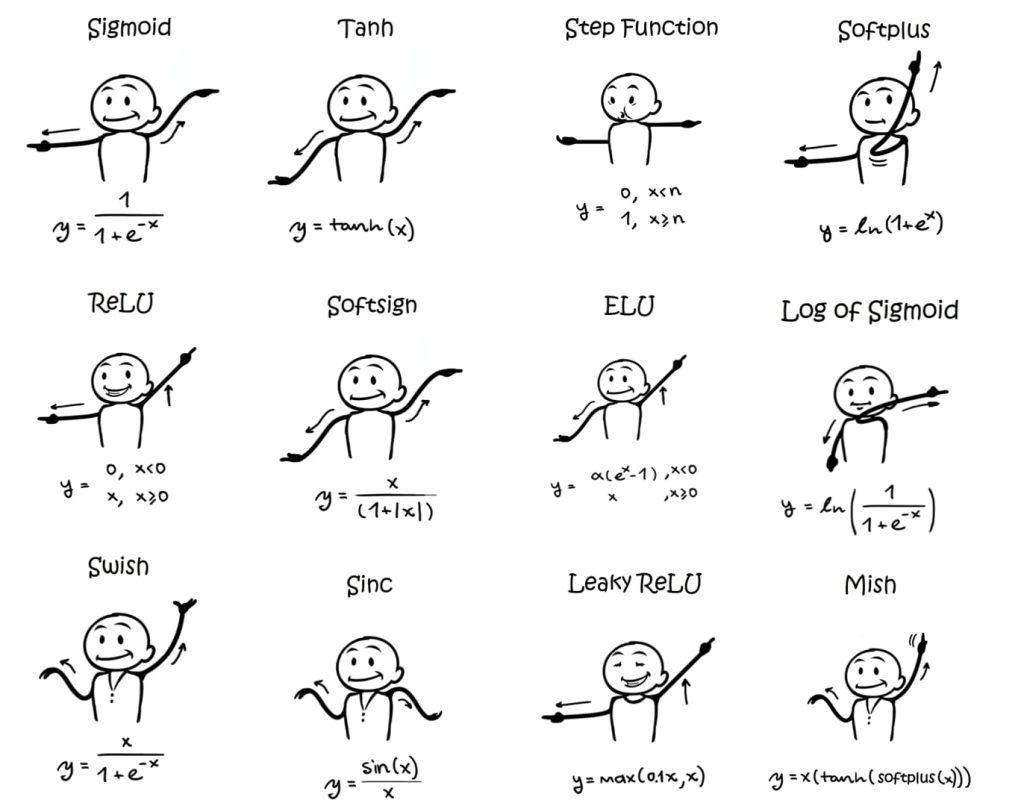
8.2. 模型
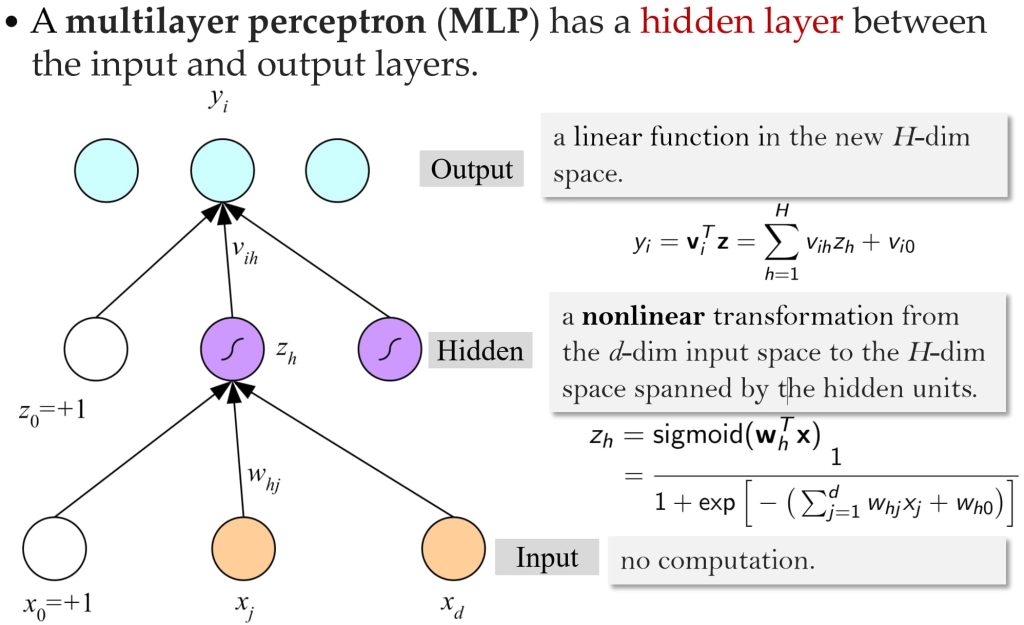
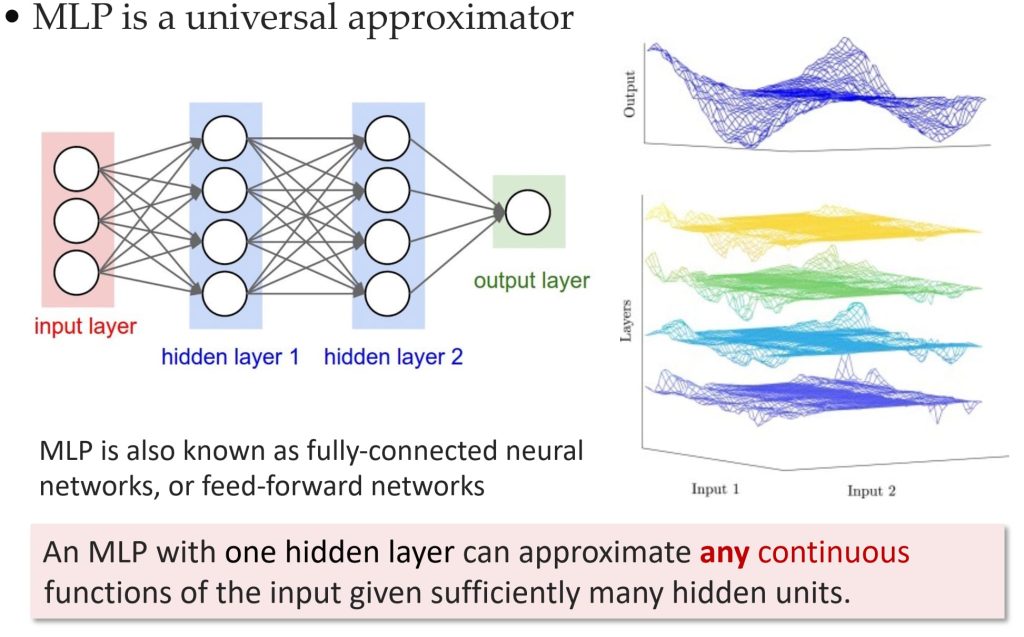
- 实现了连续的(可微分的)决策,使得优化变得更加容易;
- 通过缩放、压缩和变形来转换非线性特征空间,并在新的空间中找到线性边界
8.3. 训练
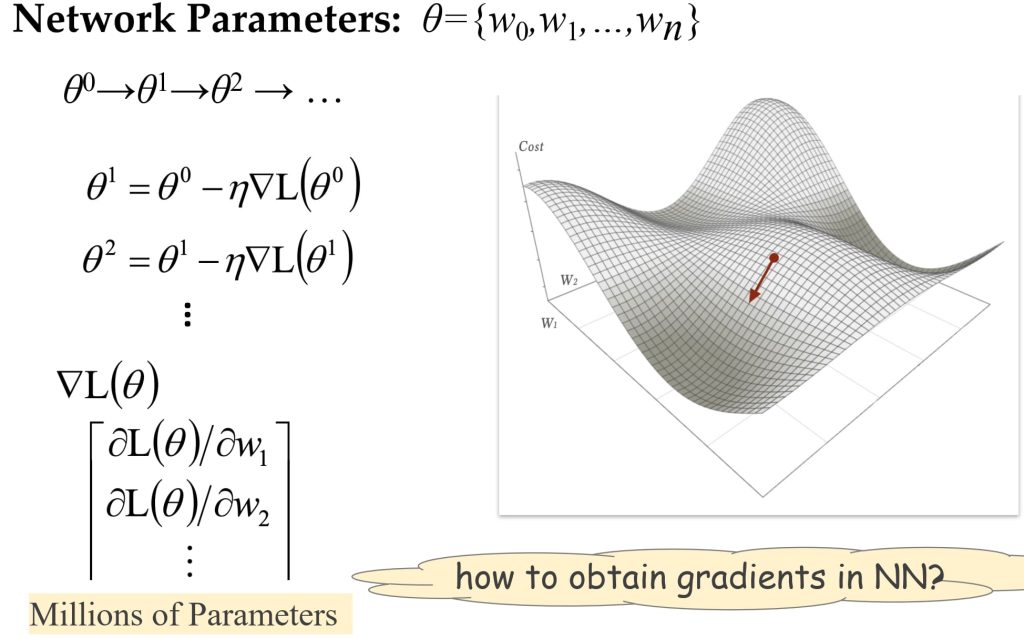
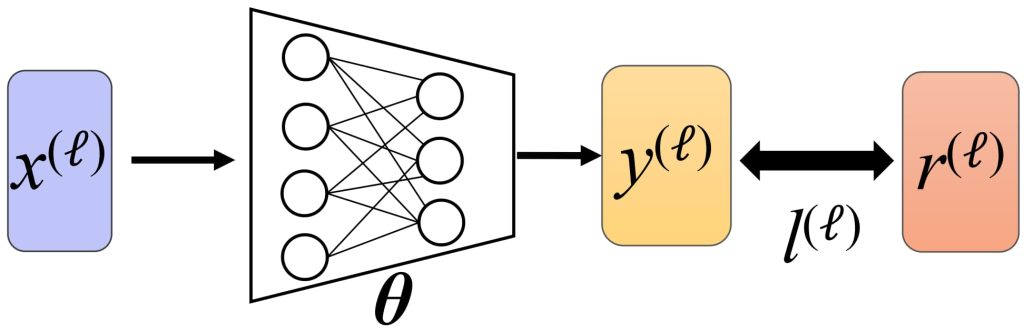
训练的核心就在于算梯度:通过误差找局部极小值点,让 θ 朝着梯度的反方向移动步长(梯度下降法)。
- 回归问题中的损失函数:
- 给定数据集 \(D = \{(x^{(ℓ)},r^{(ℓ)})\}_{ℓ=1}^N\),其中 \(x^{(ℓ)}\) 是输入,\(r^{(ℓ)}\) 是对应的目标值。
- 模型通过参数 θ 对每个 \(x^{(ℓ)}\) 预测值 \(y^{(ℓ)}\)。
- 目标是最小化均方误差(MSE)损失:
- \(\mathcal{L}(\theta \mid D) = \frac{1}{2} \sum_{\ell=1}^N \sum_{i=1}^m \left( r_i^{(\ell)} – y_i^{(\ell)} \right)^2\),其中 m 即输出值得维度。
- 单样本损失函数(通常认为样本间是独立的):
- 整个数据集的损失函数可以表示为:
- \(\mathcal{L}(\theta \mid D) = \sum_{\ell=1}^N \ell^{(\ell)}(\theta) \Rightarrow \frac{\partial \mathcal{L}(\theta \mid D)}{\partial w} = \sum_{\ell=1}^N \frac{\partial \ell^{(\ell)}(\theta)}{\partial w}\);
- 这里 \(\ell^{(\ell)}(\theta)\) 是单个样本的损失函数。
- 对于单训练样本 (x, r):
- \(\ell(x, r) = \frac{1}{2} \sum_{i=1}^m \left( r_i – y_i \right)^2\)。
- 整个数据集的损失函数可以表示为:
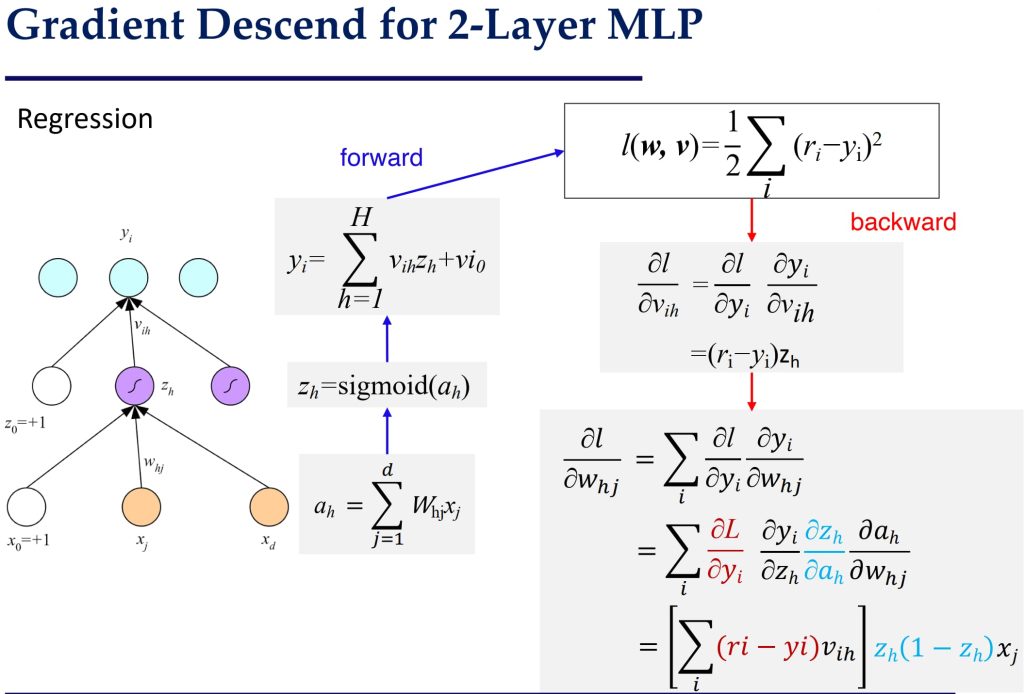
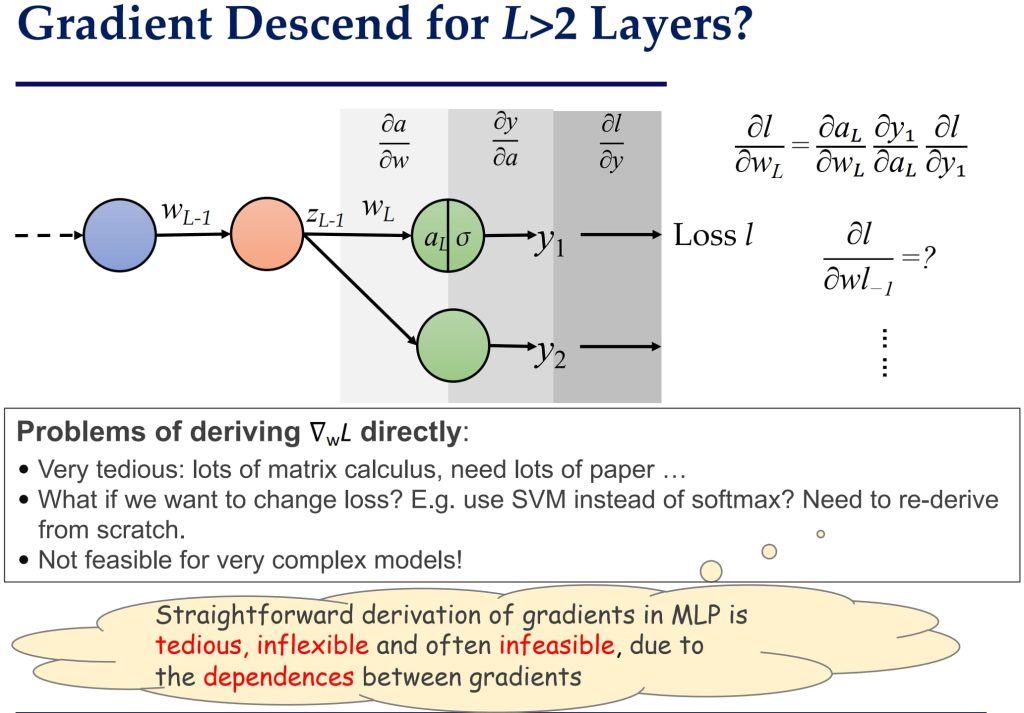
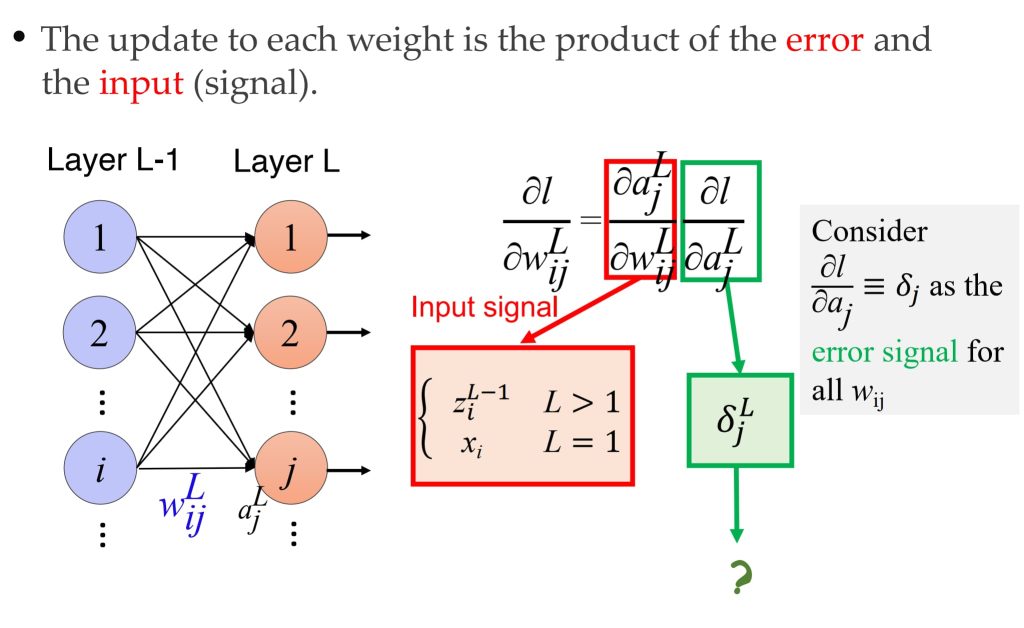
8.4. 误差反向传播(Error Backpropagation)
由于直接计算过于复杂,因此反向传播(Backpropagation)是一个高效的计算梯度的方法。
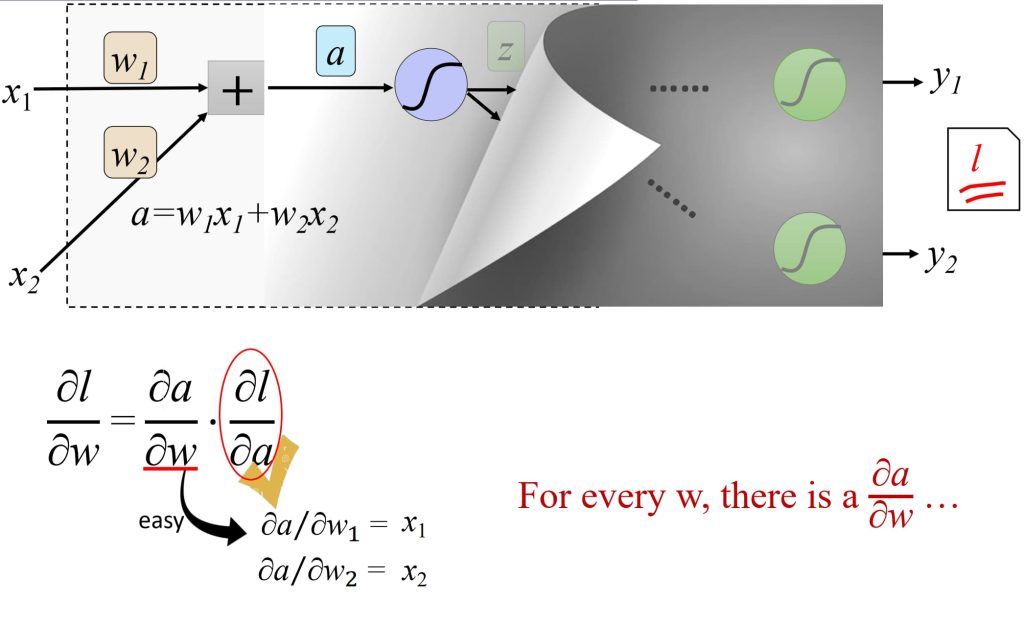
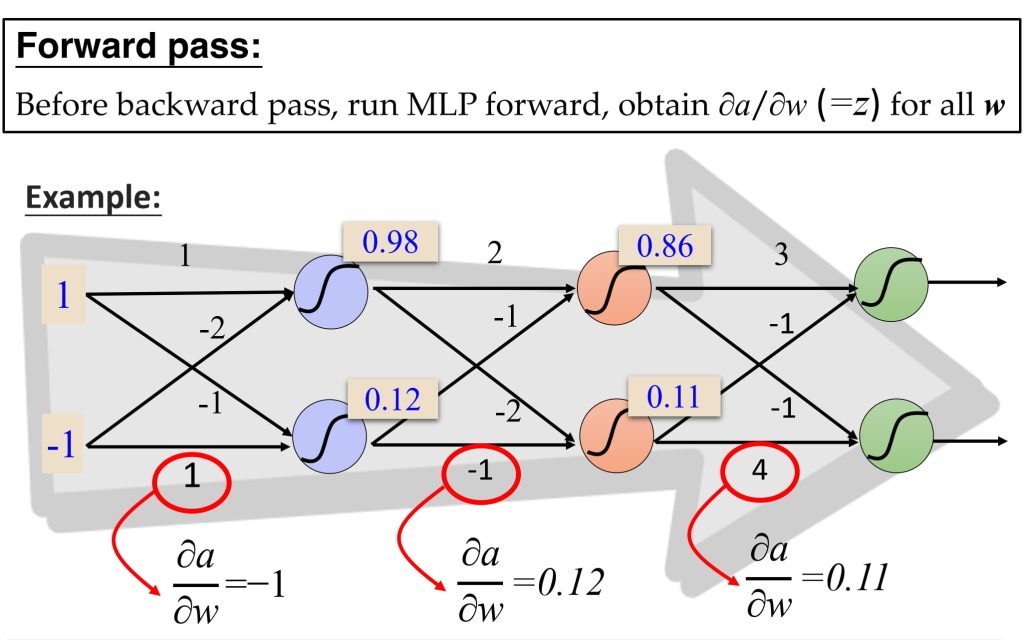
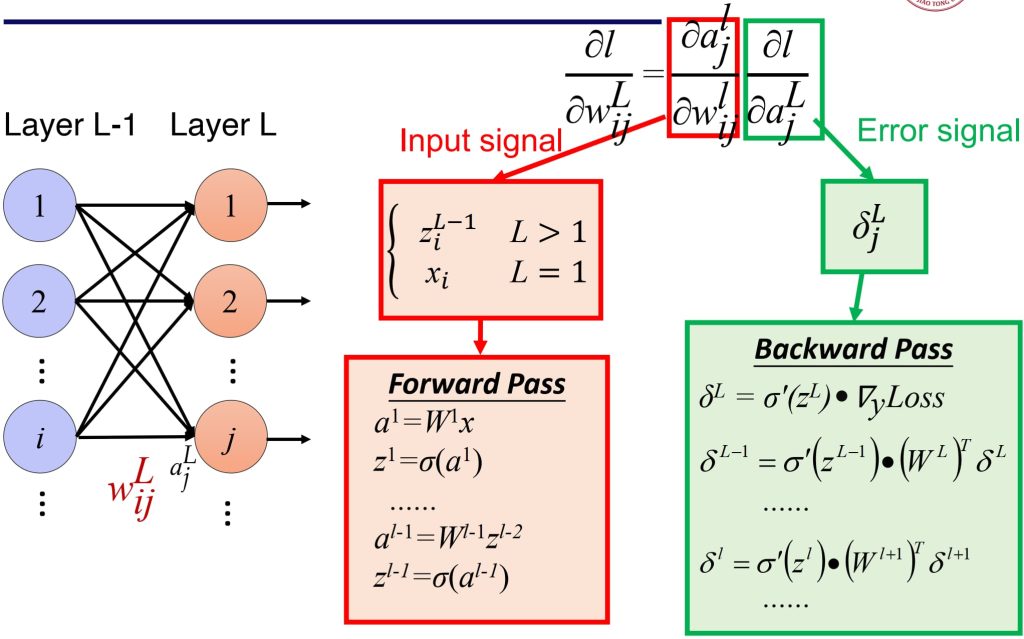
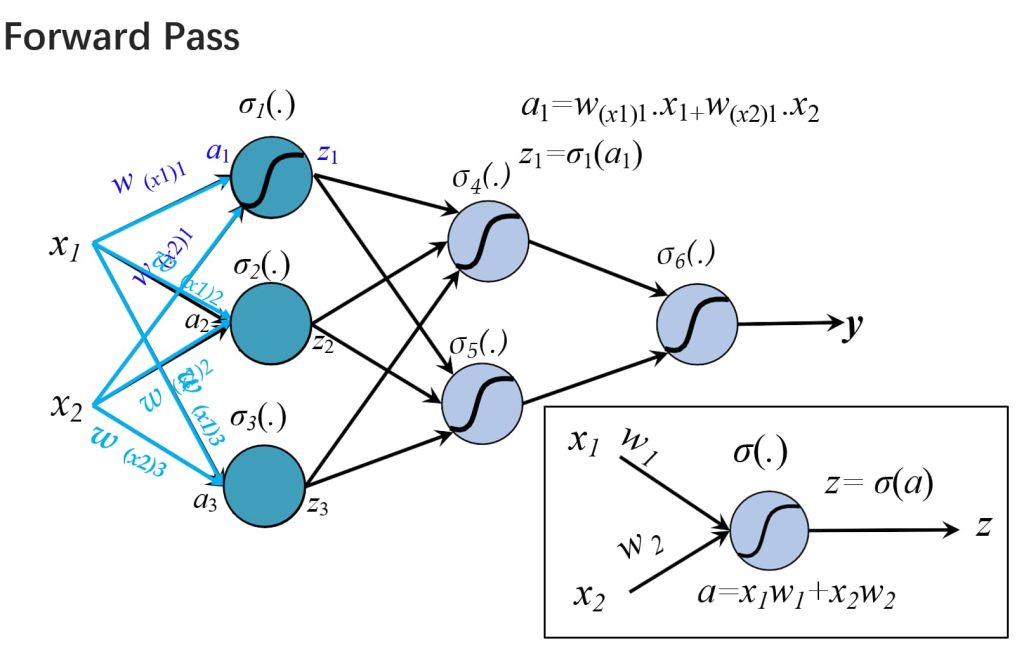
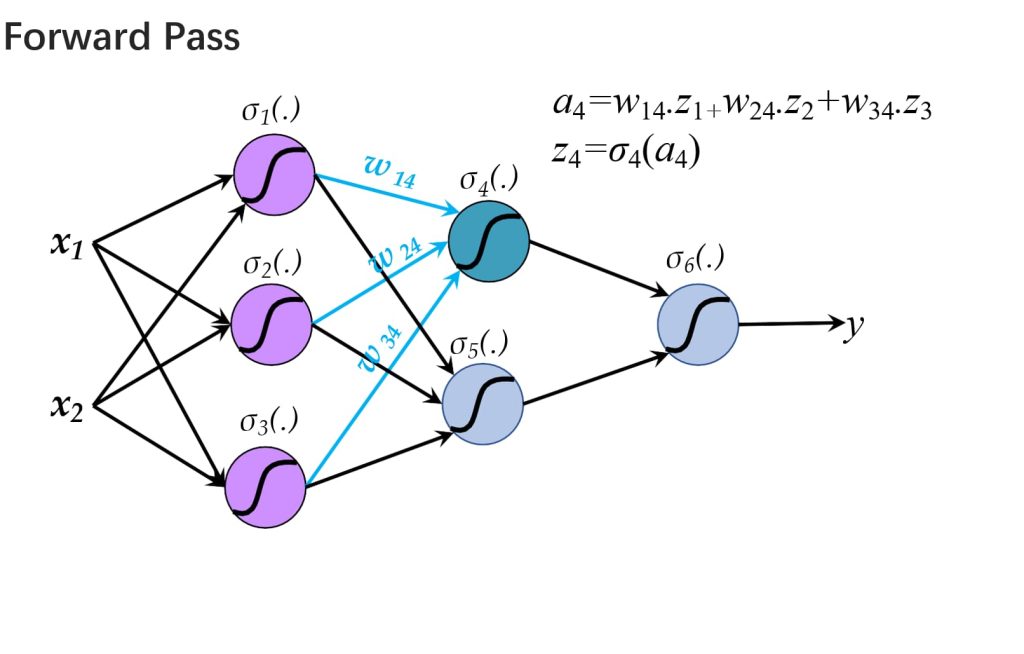
- 前向传播(Forward Propagation):
- 将输入向量应用于网络,并计算所有隐藏层和输出层单元的激活值。
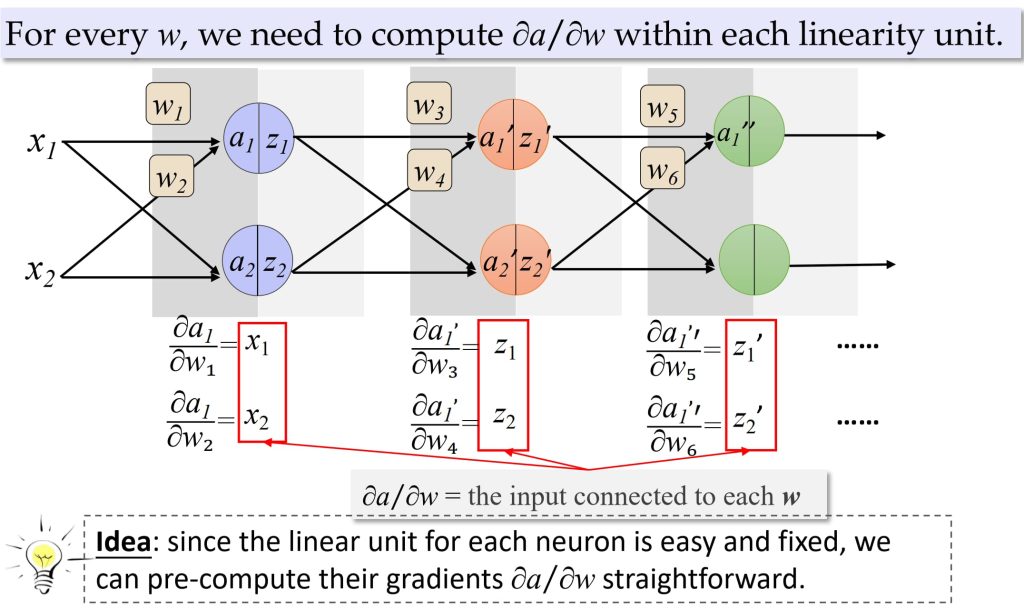
- \(a_j = \sum_i w_{ji} z_i, \quad z_j = \sigma(a_j), \quad j = 1, \dots, d\)
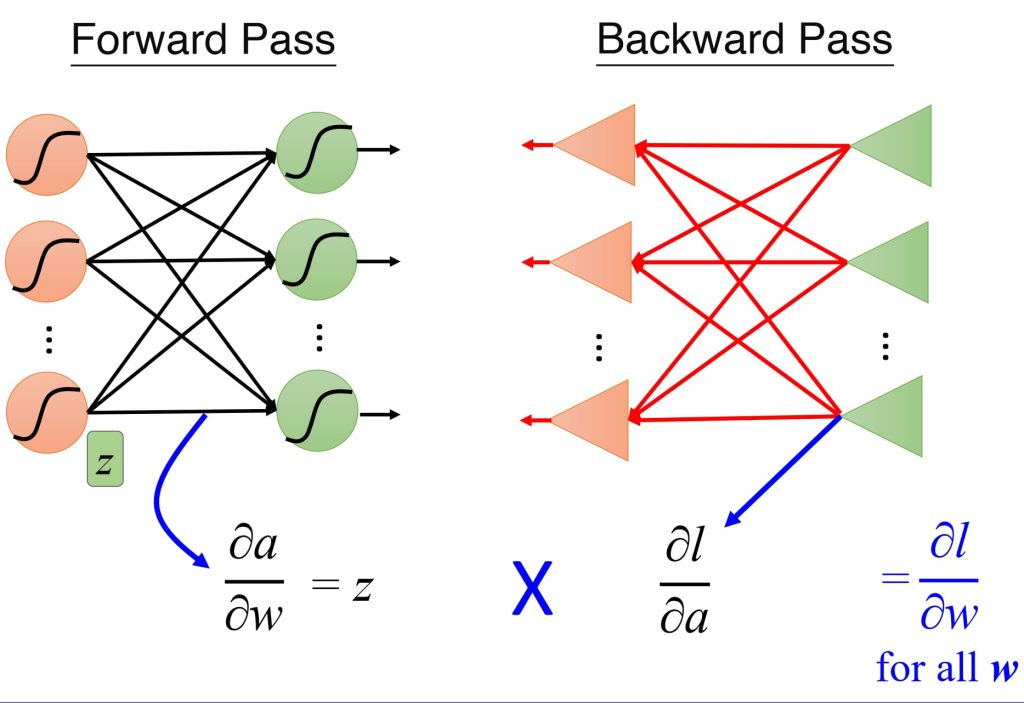
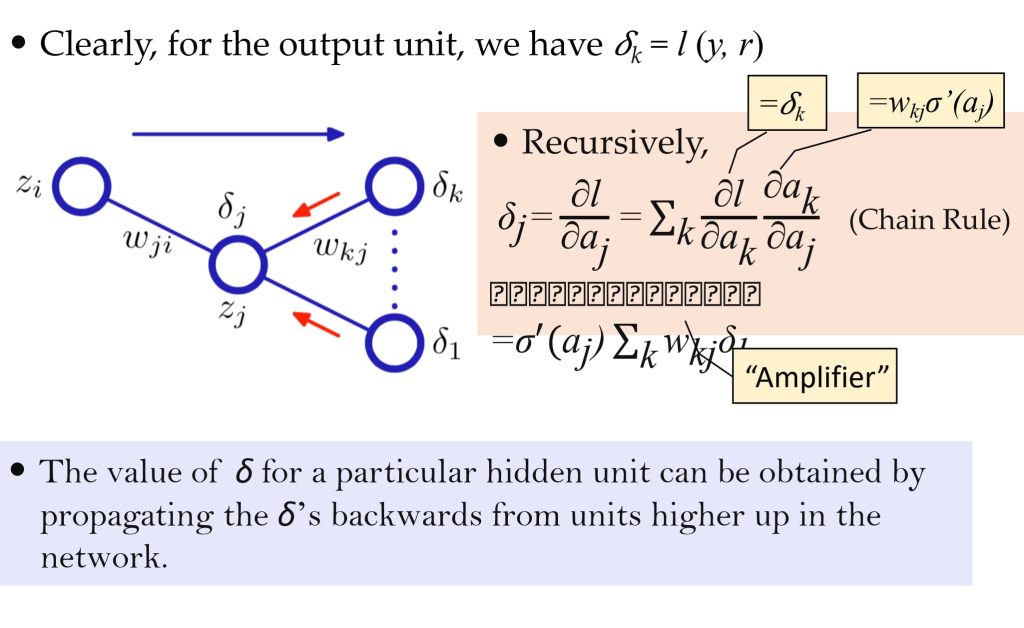
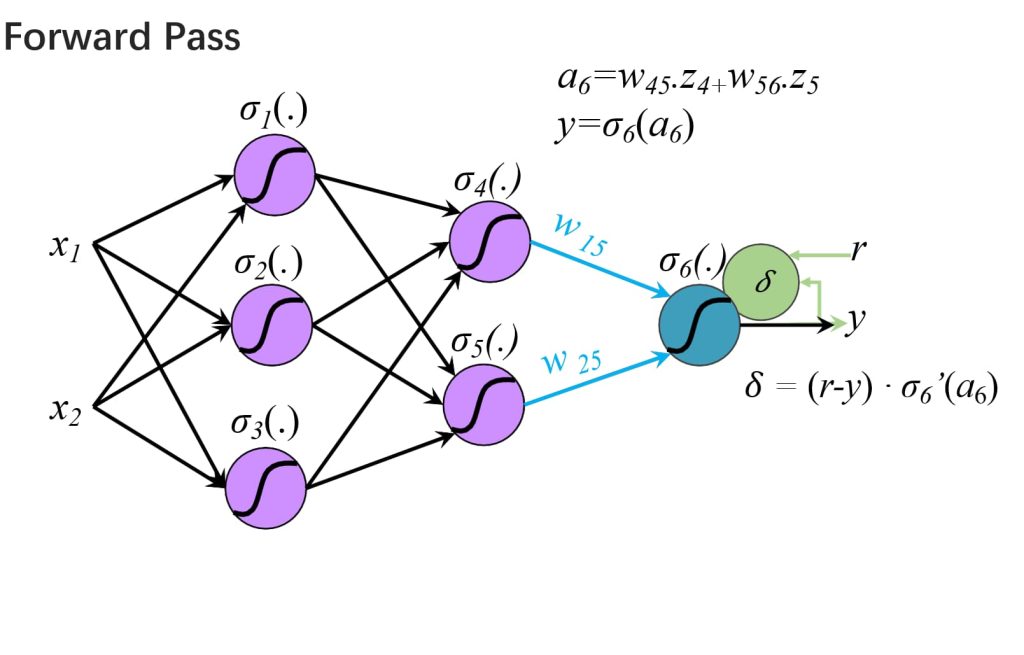
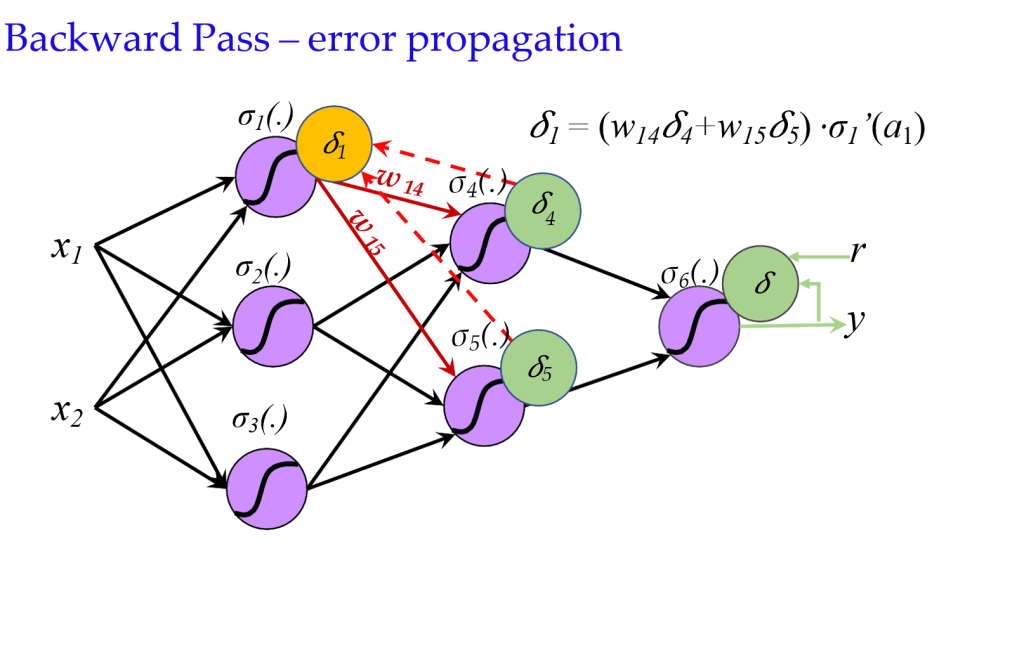
- 反向传播(Backward Propagation):
- 计算损失函数对权重的导数(误差),误差通过网络向后传播。
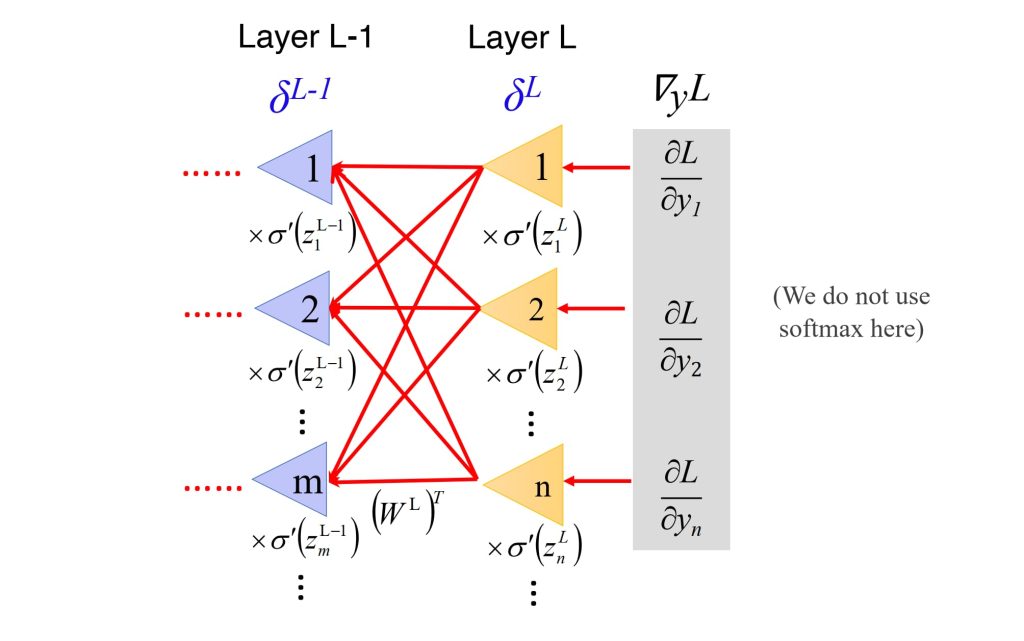
- \(\delta_j^L = \frac{\partial l}{\partial a_j}\)
- \(\delta^{L-1} = \sigma'(z^{L-1}) (\mathbf{W}^L)^T \delta^L\)
- 参数更新
- 使用计算出的导数(误差)来调整参数。
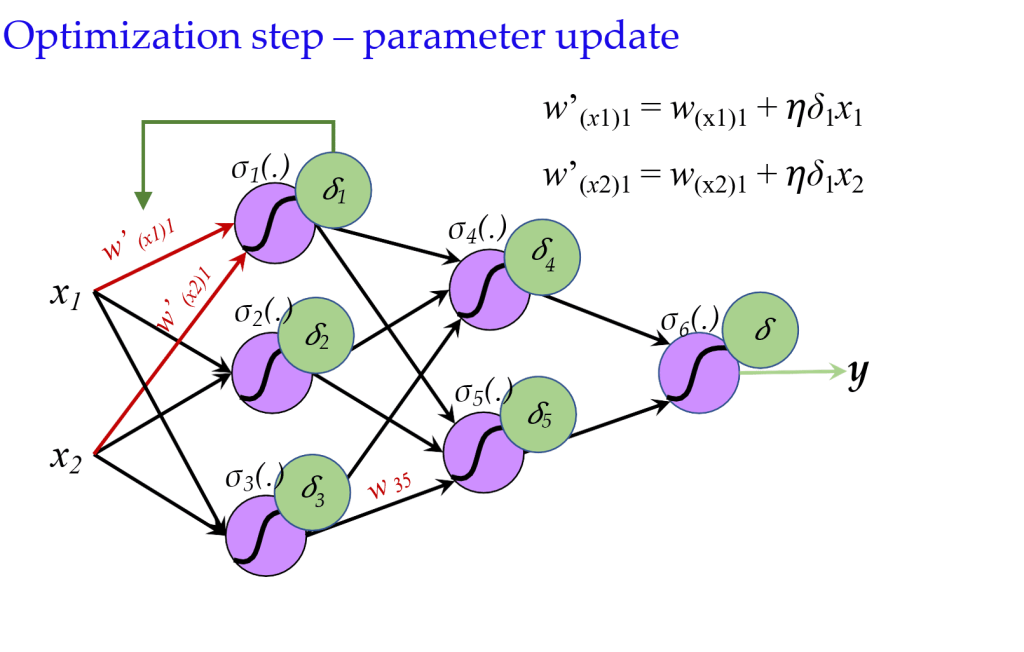
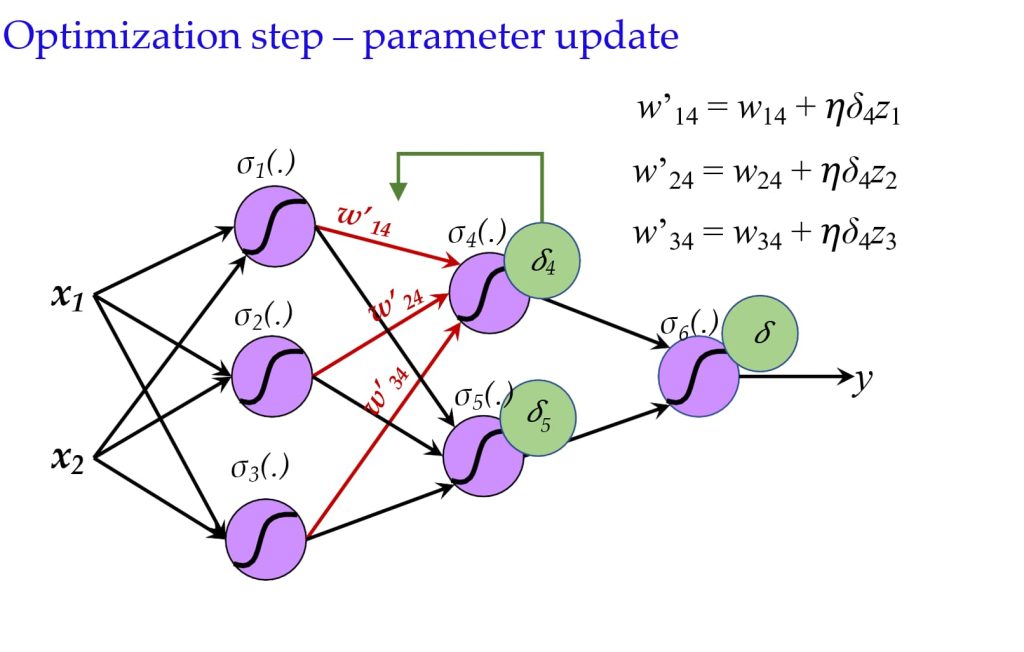
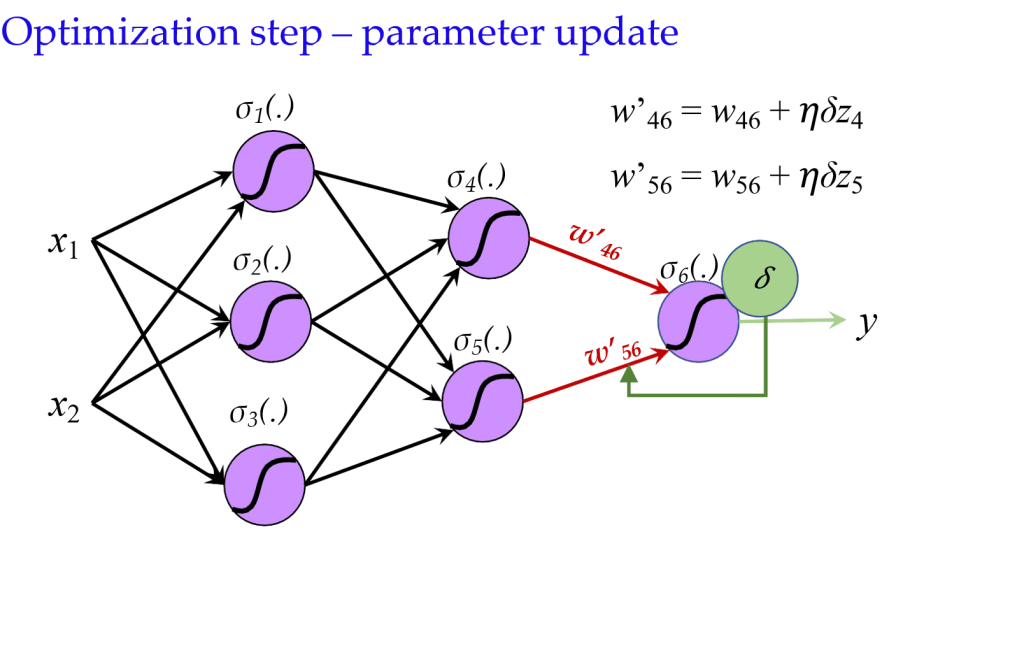
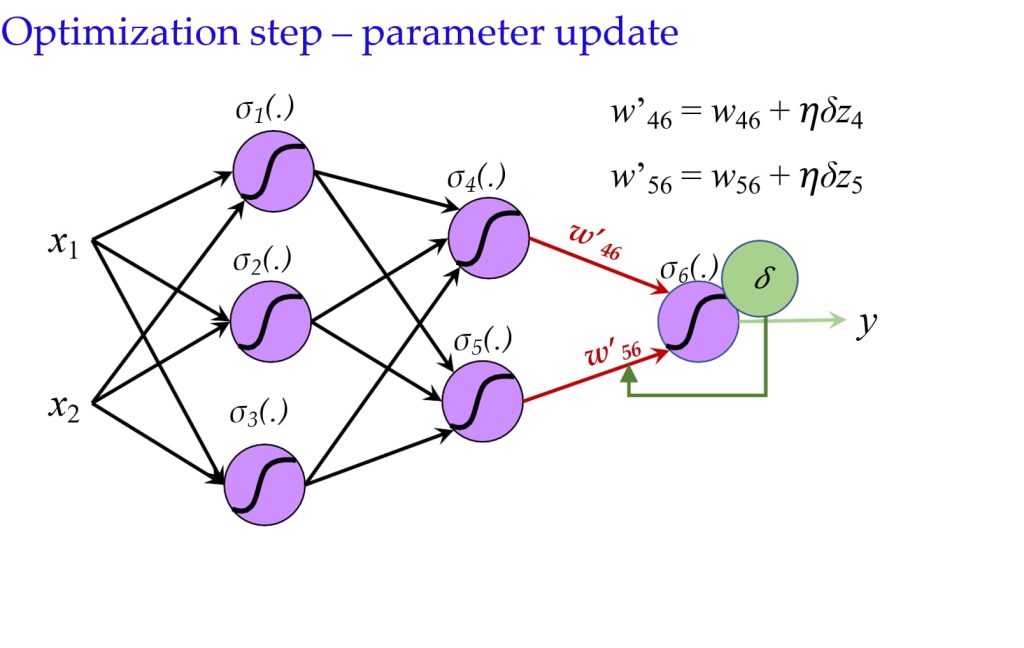
- \(w’_{ij} = w_{ij} + \eta \delta_j z_i\)
8.4.1 反向传播过程:
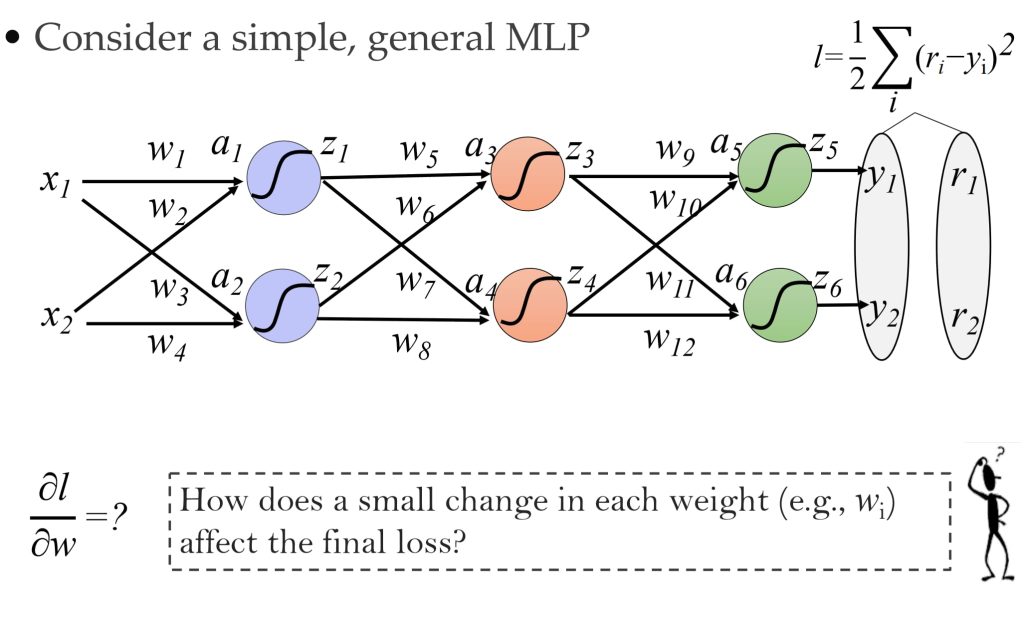
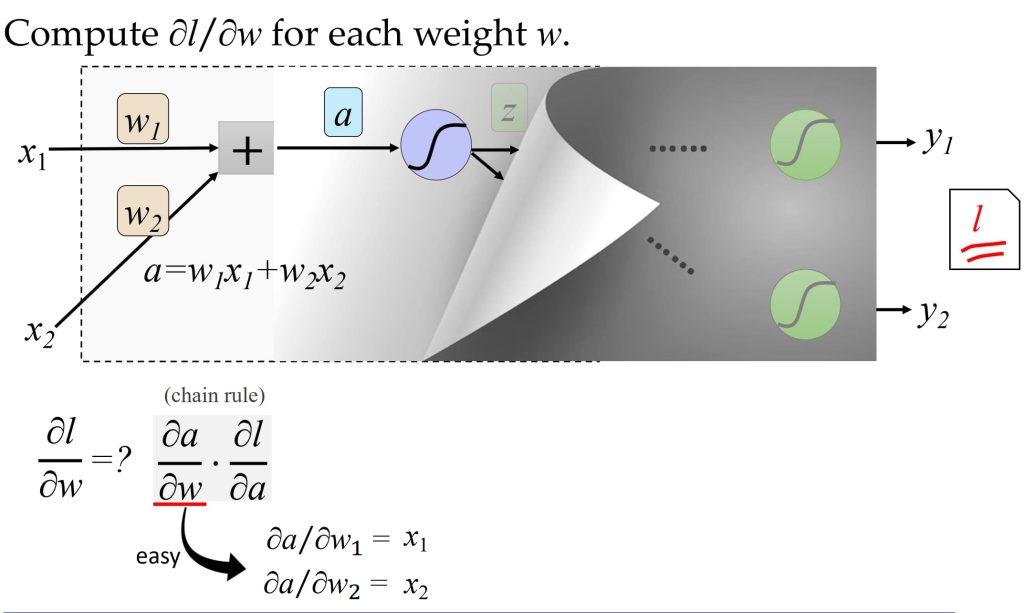
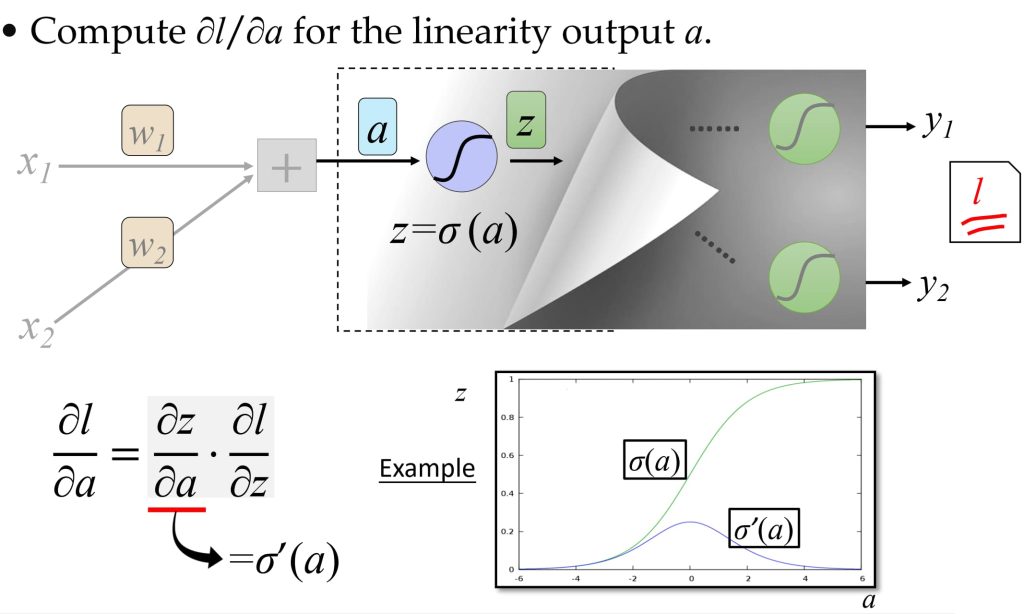
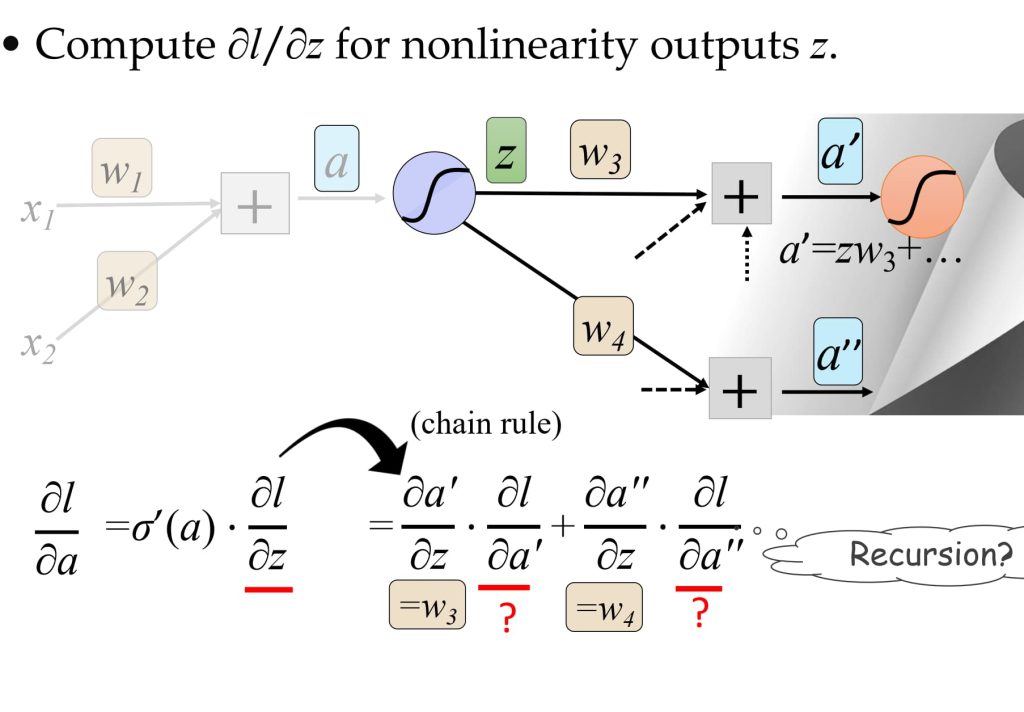
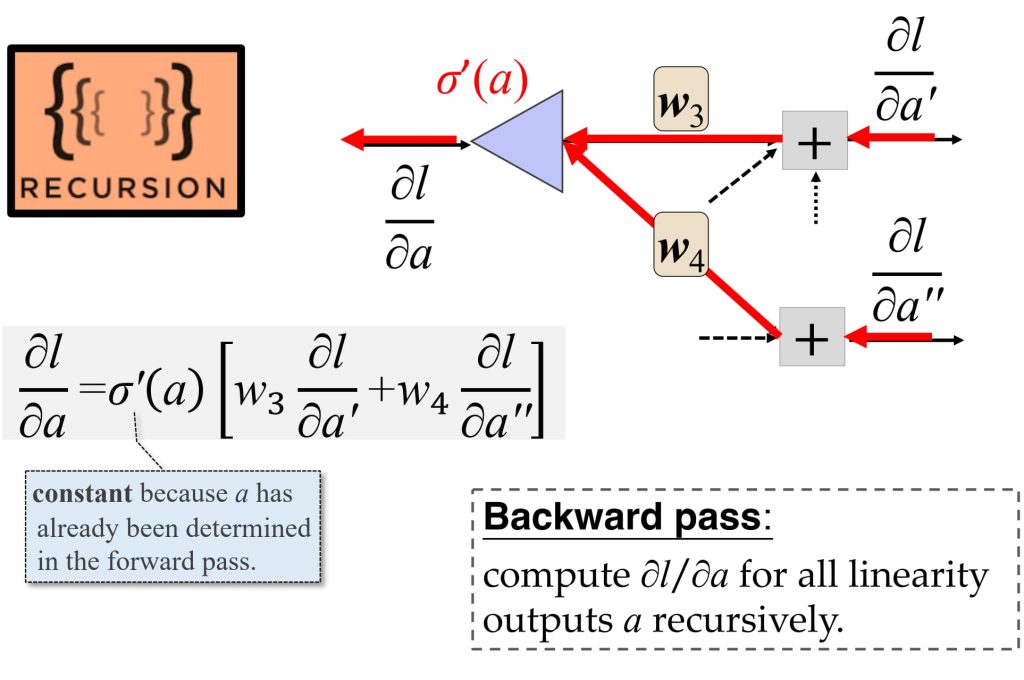
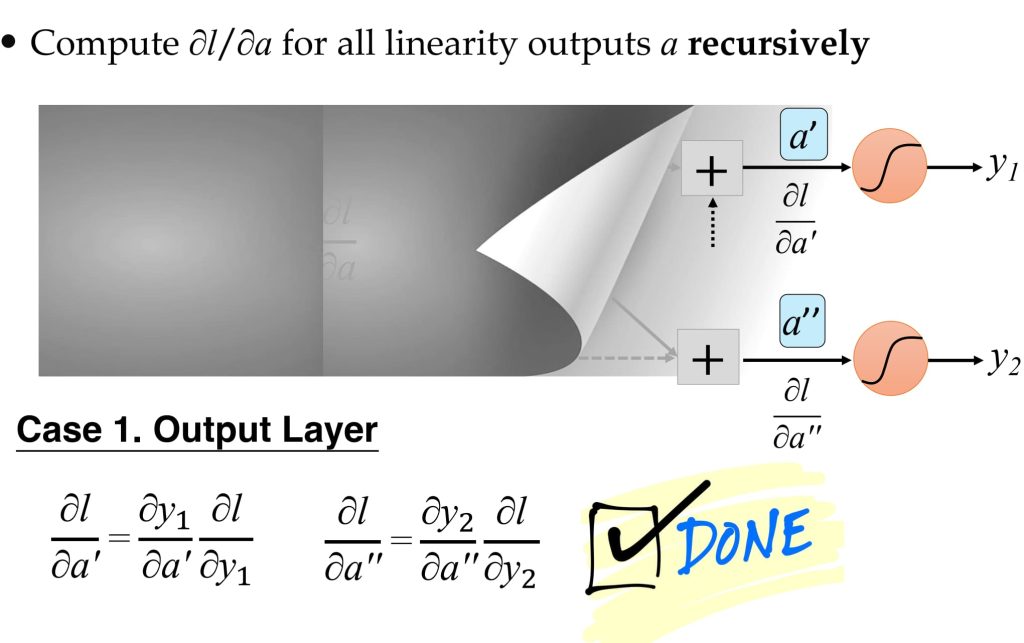
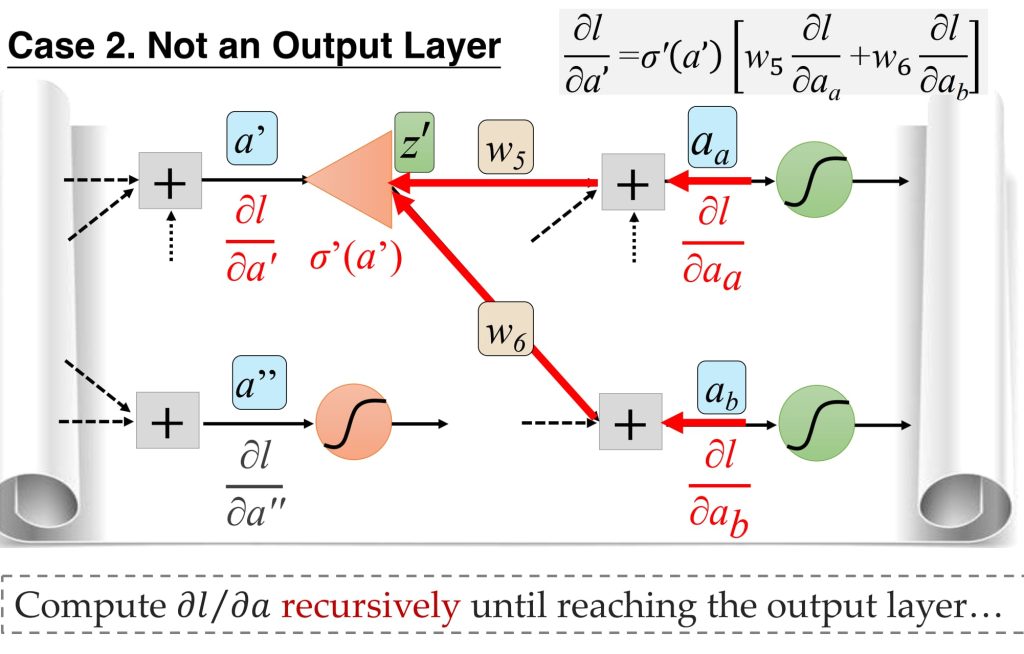
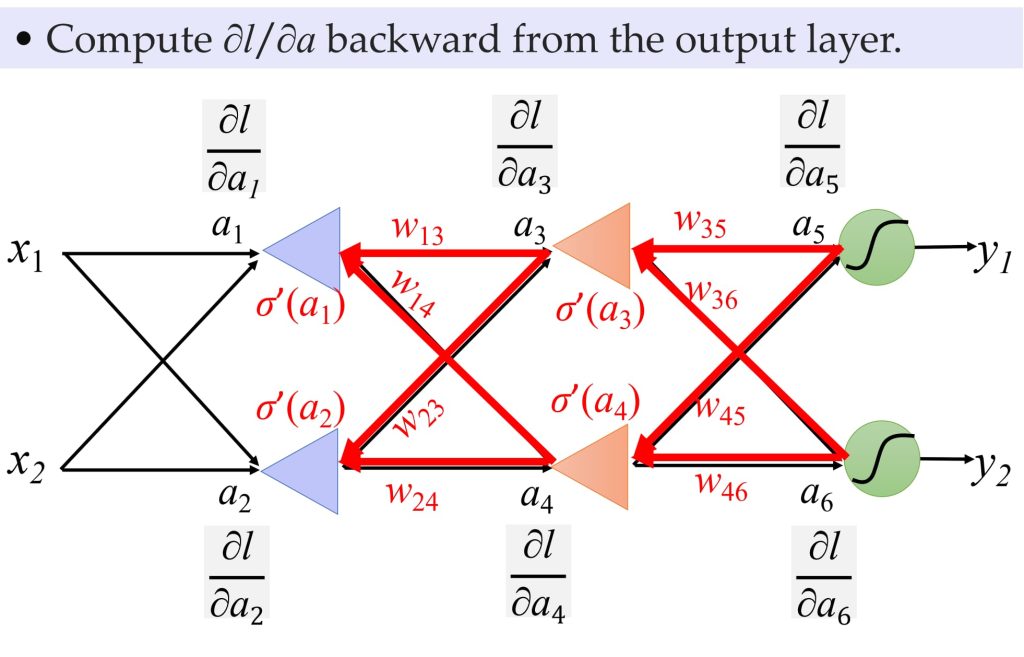
8.4.2. 基于误差传播的视角
8.4.3. BP 的示例
8.5. 神经网络(Neural Networks)和模组化(Modularization)
- 神经网络的表达能力
- 任何连续函数 \(f: R^N \rightarrow R^M\),都可以通过一个隐藏层的神经网络表示(前提是有足够的隐藏神经元),神经网络具有通用函数逼近能力。
- 深度 vs. 浅层网络
- 浅层网络可以表示任何函数,但深层结构更有效。
- 深度网络在相同参数数量下,通常比浅层网络表现更好。
- 模块化思想
- 模块化设计:将复杂任务拆分为多个基本分类器或子模块。
- 示例:图像分类任务可以分解为多个子任务(如“性别分类”和“发型分类”),每个子模块可以独立训练。
- 模块化的优点:每个分类器可以利用充足的训练数据,减少整体复杂度,子模块可以复用,提升效率。
- 深度网络中的自动模块化
- 初始层提取基本特征。
- 后续层逐步组合特征,形成更高级的分类器。
- 这种自动模块化有助于减少训练数据需求。
8.6. 深度学习(Deep Learning)
- 定义:深度学习(Deep Learning,简称 DL = Learning Feature Representations)是机器学习的一个分支,核心是学习数据表征,通过使用具有复杂结构或多层非线性变换的模型架构,尝试对数据中的高层次抽象进行建模的算法集合。
- 核心概念:深度学习是一种自动学习特征表示的方式,区别于传统机器学习需要手工设计特征;它通过可训练的特征提取器和分类器实现端到端学习(End-to-end Learning,模型学习从初始输入阶段到最终输出结果的所有步骤)。
- 层次化表示(Hierarchical Representations):深度学习通过多层结构逐步将输入数据转换为高层次的抽象表示;低层特征更通用,高层特征更具语义性和更具不变性。
- 深度神经网络类型,常见架构包括:前馈神经网络(Feedforward Neural Networks),卷积神经网络(CNN),循环神经网络(RNN),Transformer模型。
- 前馈神经网络(深度的 MLP)的局限性:难以训练(梯度消失、梯度爆炸、参数过多);输入不变性问题(对输入过于敏感,比如图片一旋转就会导致很大影响);缺乏空间信息处理能力(无法有效捕捉输入数据中的空间或局部特征);通常作为中间层使用(用于特定任务的特征提取或信号转换)。
- 替代方案:卷积神经网络(CNN):适合图像处理;循环神经网络(RNN):适合序列数据;Transformer:适合各种任务,包括自然语言处理。
9. 语言模型(Language Model)
9.1. 词嵌入(Word Embedding)
- 如果沿用计算机 ASCII 码的表示方式,机器无法理解数字的意义,无法理解单词与单词间的关系;
- One-hot 向量:对于词汇表来说,向量的维度等于词汇表的大小,极为浪费,且单词间向量正交,依然无法学习语义;
- 期望:使用低维度、稠密且能反映语义相似度和单词间关系结构的压缩向量嵌入方式。
Word2vec 是一个学习词向量的框架
- 思想:
- 词向量初始化:为固定词汇表中的每个词分配可学习的向量。
- 上下文建模:遍历文本中每个位置 t,确定中心词 c 和上下文词 o。
- 概率计算:根据词向量的相似性,计算上下文词 o 在给定中心词 c 时(或反向)的概率。
- 优化更新:不断调整词向量,最大化上述概率。
9.2. Mikolov’s CBOW(Continuous-Bag-of-Words) 词袋模型
- 通过结合上下文词(周围词)的分布式表示,预测中间的目标词。
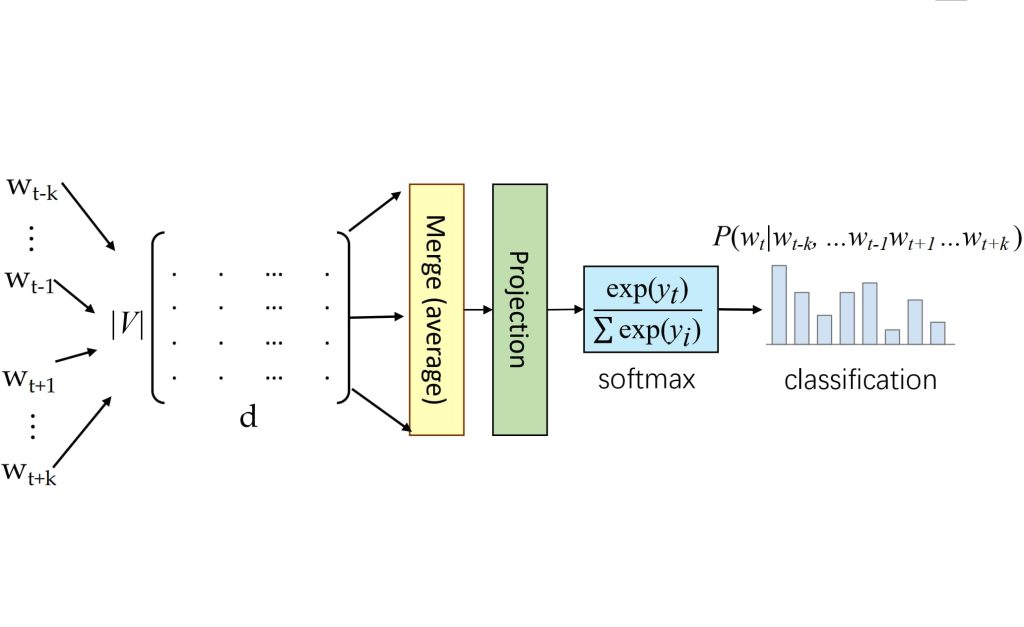
- 公式:\(P(w_t \mid w_{t-k}, \dots, w_{t-1}, w_{t+1}, \dots, w_{t+k}) = \text{softmax}\left(\text{NN}\left(V(w_{t-k}) + \dots + V(w_{t+k})\right)\right)\)
- 其中,使用上下文词的词向量 V 的加和,通过神经网络(NN)计算目标词 \(w_t\) 的概率。
- 神经网络表示:
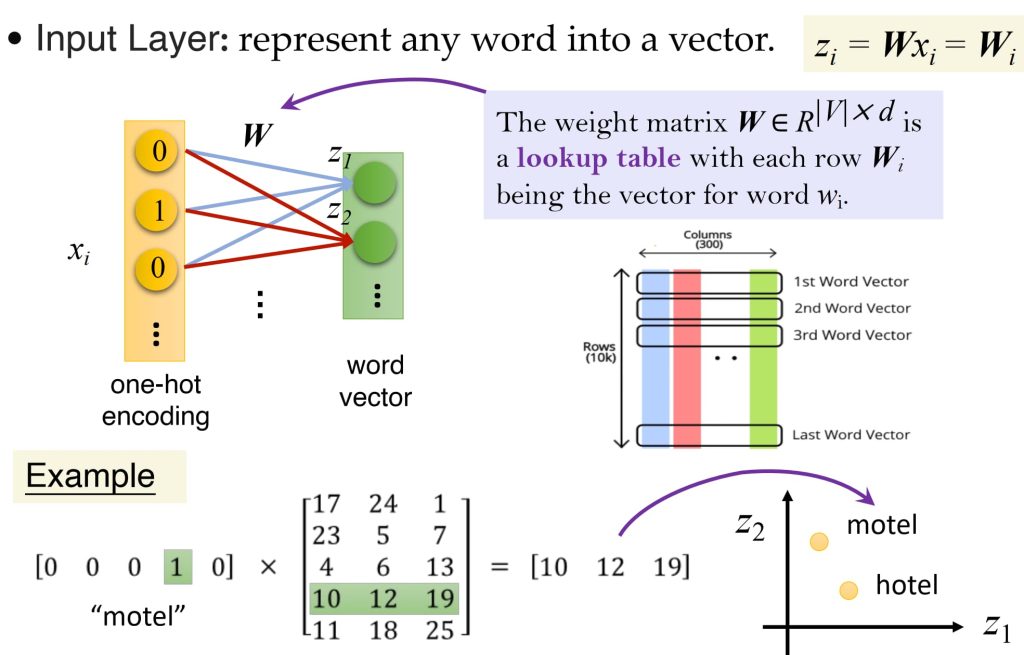
- 输入层:将每个词的独热表示(one-hot)转换为稠密向量。
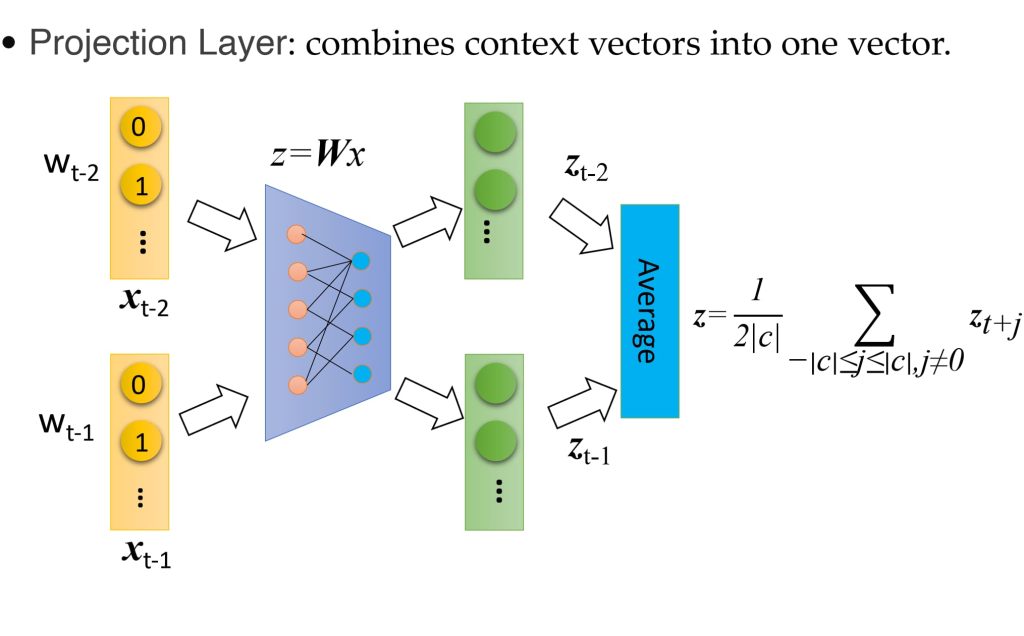
- 投影层:将上下文词的词向量组合(通常求和)。
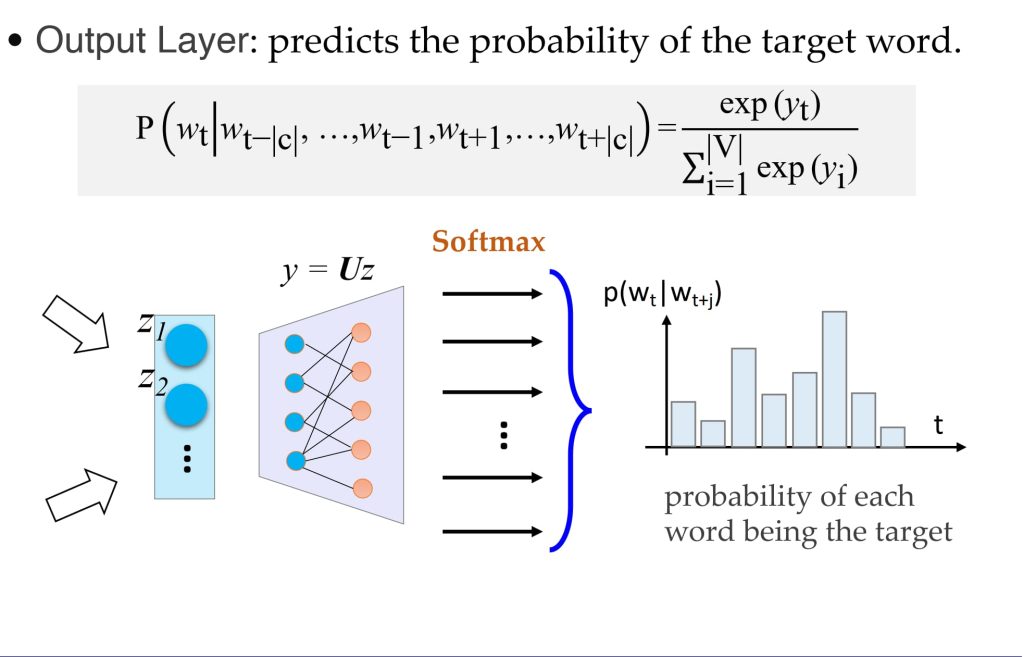
- 输出层:基于组合的上下文向量预测目标词 \(w_t\)。
- 上下文中词的顺序对投影结果没有影响
- 训练:
- 给定数据集(N 个单词) \(D = \{w_1, w_2, \dots, w_{N}\}\),最小化负对数似然 (NLL) 损失函数:
- \(L(W, U \mid D) = -\frac{1}{N} \sum_{t=1}^{N} \log p(w_t \mid w_{t-k}, \dots, w_{t-1}, w_{t+1}, \dots, w_{t+k})\) ,使用梯度下降
9.3. 语言模型
- 定义:语言模型的目标是估计一个句子或词序列 \(x=(w_1,w_2,…,w_N)\) 的概率 \(p(x) = p(w_1,w_2,…,w_N)\)。
- 计算概率的方式:
- 链式法则:\(p(w_1, w_2, \dots, w_N) = p(w_1) \cdot p(w_2 | w_1) \cdot p(w_3 | w_1, w_2) \cdots p(w_N | w_1, w_2, \dots, w_{N-1})\)
- 马尔科夫假设(仅考虑前 n – 1 个词):\(p(w_i \mid w_1, w_2, \dots, w_N) \approx p(w_i \mid w_{i-n+1}, \dots, w_{i-1})\)
- Bigram 模型:
- n = 2 的特殊情况,即只考虑当前词和前一个词的关系:
- \(p(w_1, w_2, \dots, w_N) \approx p(w_1) \cdot p(w_2 | w_1) \cdot p(w_3 | w_2) \cdots p(w_N | w_{N-1})\)
- 如何预测这些条件概率:
- naïve 的想法:直接计数。缺点:依赖离散符号表示,面临数据稀疏问题(Data Sparsity);实际没有学习到语义;对相关词和句子不敏感,对前缀变化极其敏感。
- 用词向量替代单词:语义和相似度问题解决,但仍未解决顺序关系问题。
- 将词向量进行拼接:引入了上下文信息,但输入的长度不可变,标点符号等对其影响较大。
- 要求:处理可变长度的序列,跟踪长期依赖关系,维护序列的顺序信息,在整个序列中共享参数。
9.4. 循环神经网络(Recurrent Neural Networks,RNN)
- 对于标准神经网络来说,一次只能处理一个单词。
- 设想是否可以让神经网络记录处理过的单词:为隐藏层添加回路以实现记忆能力。
- 核心思想:通过递归关系将当前时间步的输入与上一时间步的隐藏状态结合,更新隐藏状态,从而逐步处理序列数据并捕获时间序列中的上下文和依赖关系。
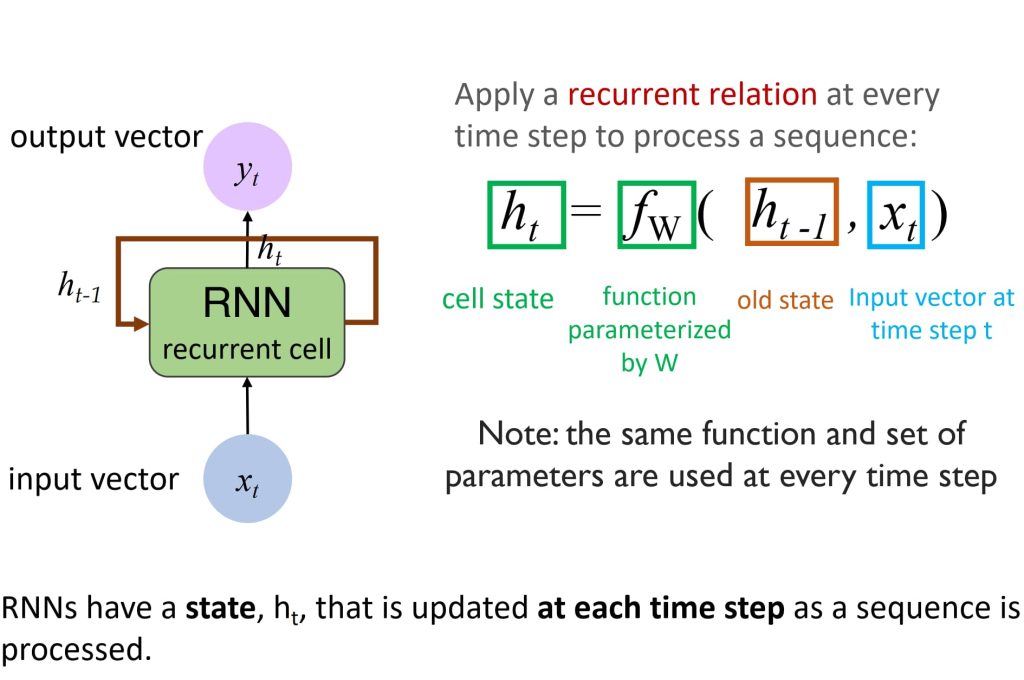
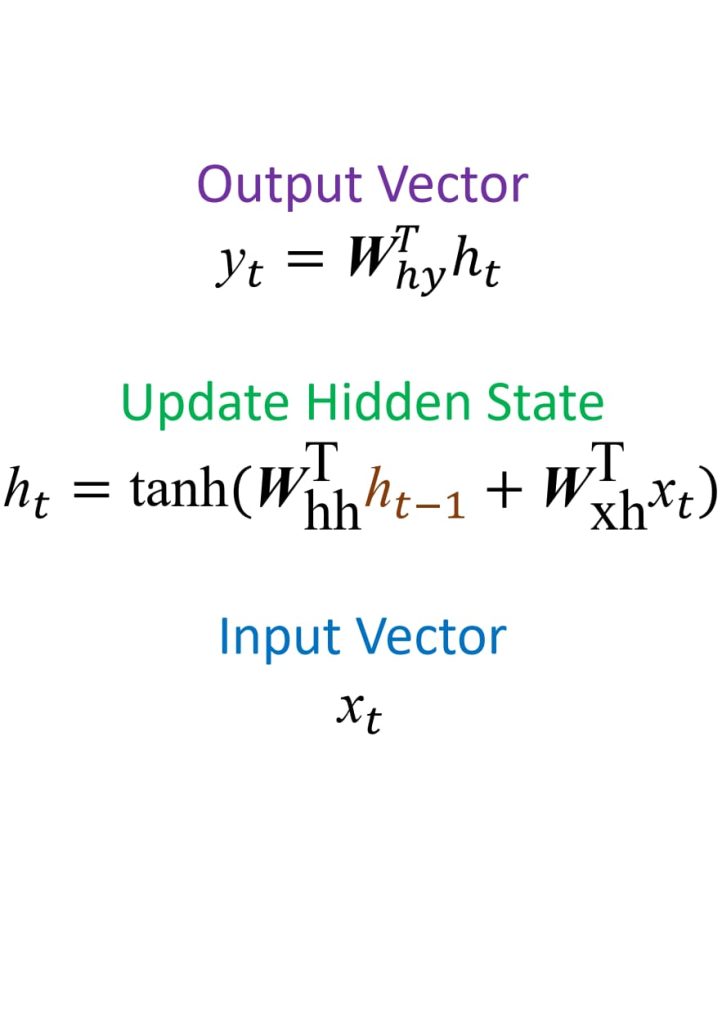
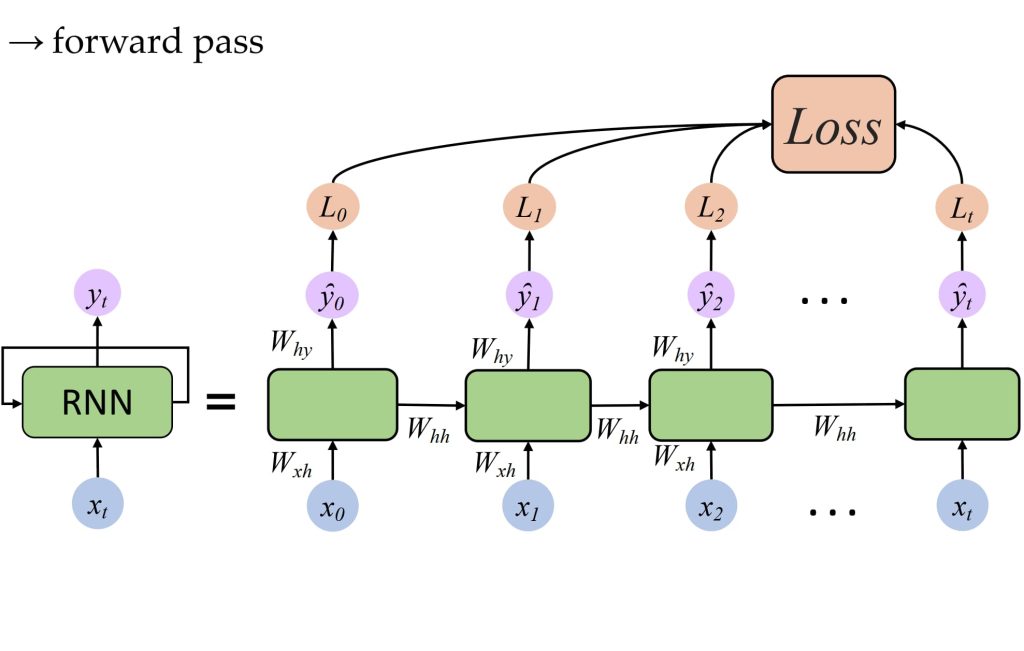
训练方法:通过时间的反向传播(Backpropagation Through Time,BPTT)
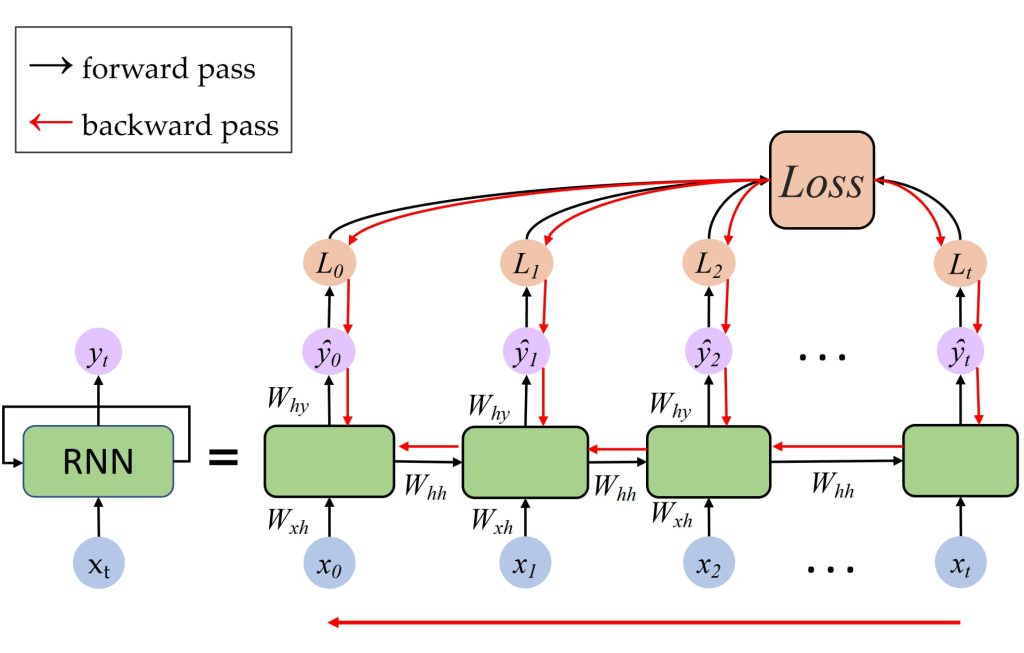
RNN 的应用:
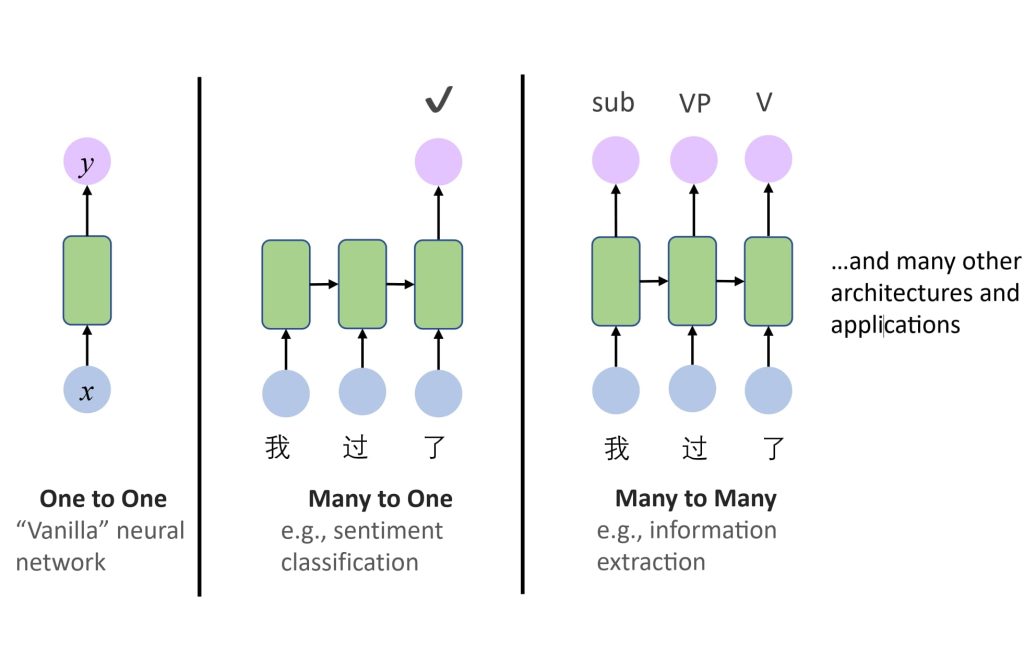
- 序列建模:
- One-to-One:传统神经网络,用于非序列数据处理。
- Many-to-One:如情感分类,将输入序列映射为单一输出。
- Many-to-Many:如信息抽取或序列生成,输入和输出均为序列。
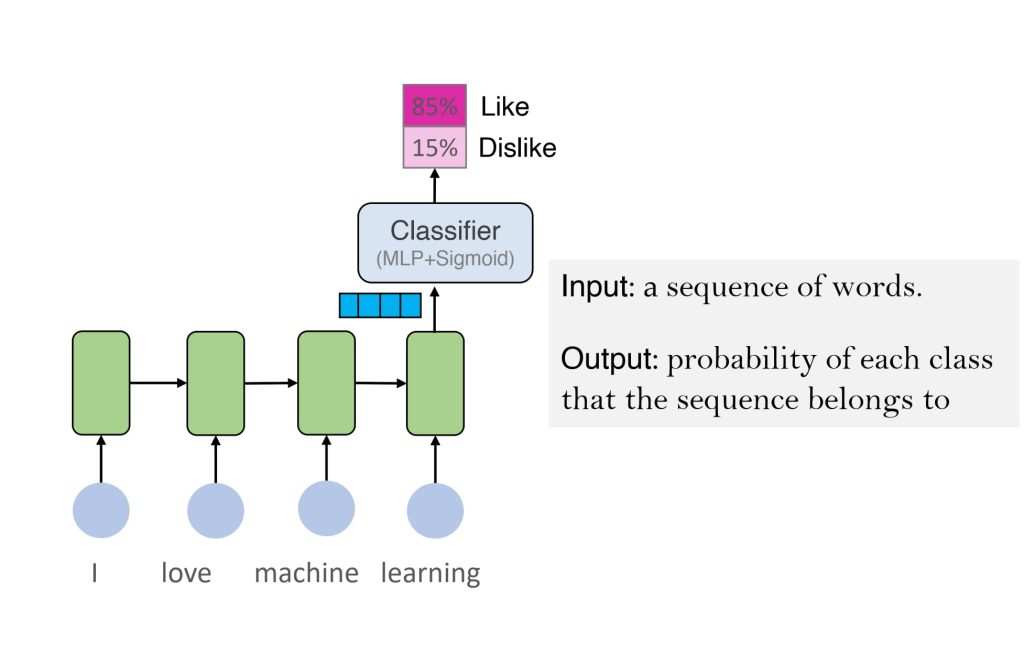
- 序列分类:
- 输入:一个序列(如单词序列)。
- 输出:序列所属类别的概率,如情感分析。
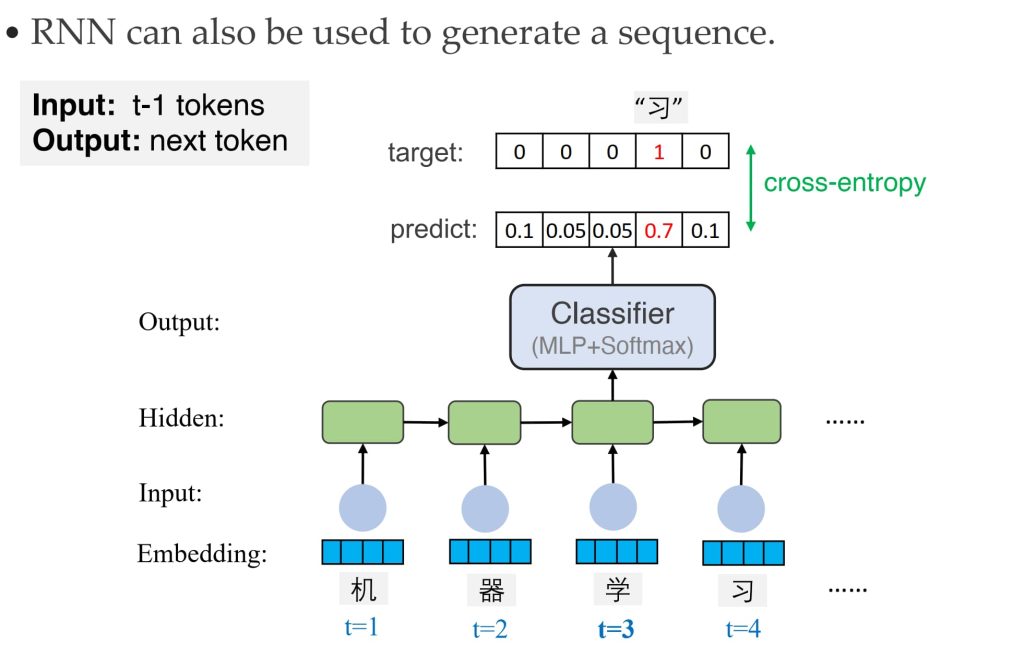
- 序列生成:
- 输入:序列的前几个时间步。
- 输出:预测下一个时间步的元素。
- 应用:诗歌生成、音乐生成等。
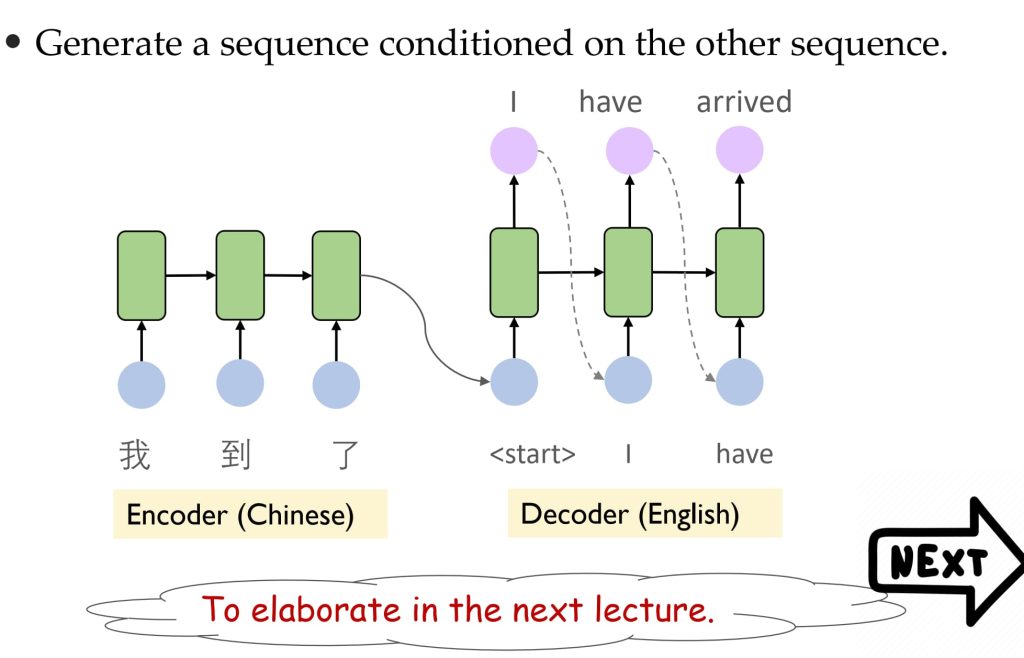
- 机器翻译:
- 输入:一个序列(如中文句子)。
- 输出:另一个序列(如对应的英文翻译)。
- 使用编码器-解码器架构处理条件序列生成任务。
优缺点:
- 优点:
- 能够捕获序列中的时间依赖关系:通过循环结构,将前一个时间步的状态(隐藏层)传递到当前时间步。
- 适用于可变长度的输入和输出:适用于广泛的序列数据处理任务。
- 共享参数,减少模型复杂度:每个时间步中共享相同的参数(权重矩阵),高效。
- 支持动态生成和预测:RNN可以在每个时间步动态生成输出。
- 能够处理上下文信息:在序列数据中,通过隐藏状态(隐层)累积和存储历史信息,当前时间步的输出可能由多个之前的时间步共同决定。
- 缺点:
- 在长序列的训练过程中,尽管 RNN 能够捕获时间依赖,但原始结构对较长序列中的远程依赖关系(如很早的时间步对当前时间步的影响)表现不佳。
- 解决方案:使用 LSTM 或 GRU,这些改进版本通过特殊的门机制缓解了记忆问题。
- 训练效率低:RNN的训练是顺序进行的(时间步之间存在依赖关系),无法并行化处理序列。
- 在长序列的训练过程中,尽管 RNN 能够捕获时间依赖,但原始结构对较长序列中的远程依赖关系(如很早的时间步对当前时间步的影响)表现不佳。
10. Transformer
序列到序列学习(Sequence-to-Sequence Learning):在自然语言处理(Natural Language Processing,NLP)领域中非常常见。
10.1. RNN 编解码器(RNN Encoder-Decoder)
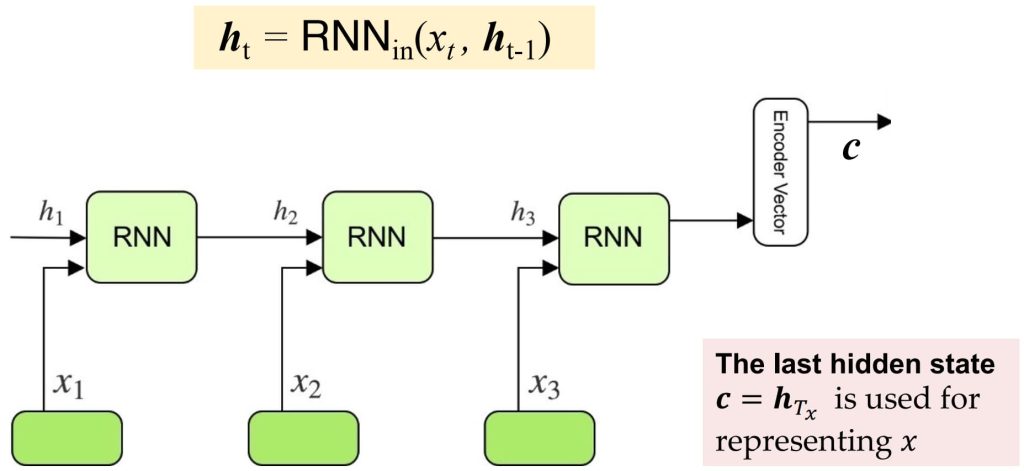
- Encoder:
- 输入序列 \(x=(x_1,x_2,\dots,x_{T_x})\) 被逐步编码为隐藏状态 \(h_t\)。
- 最后一个隐藏状态 \(h_{T_x}\) 被用作整个输入序列的压缩表示(即上下文向量 c)。
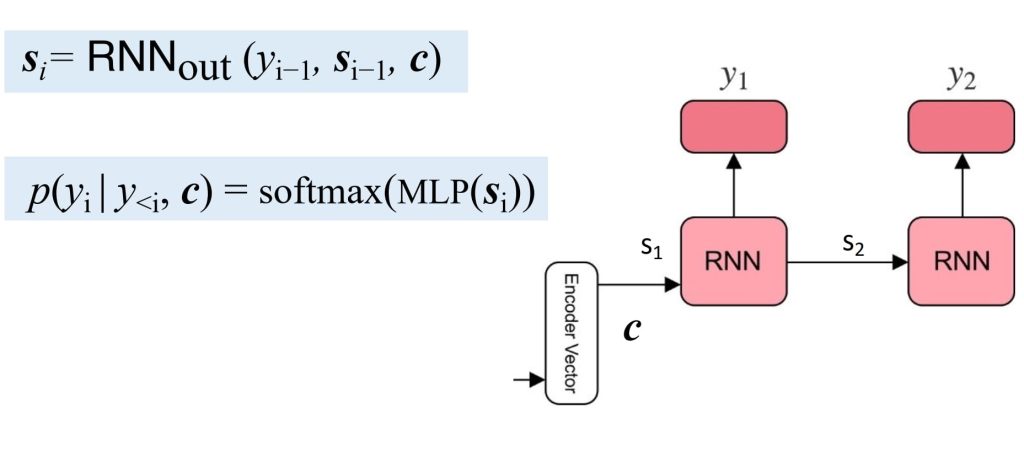
- Decoder:
- 利用上下文向量 c 和先前生成的隐藏状态 \(s_{i-1}\),预测目标序列 \(y=(y_1,y_2,\dots,y_{T_y})\) 。
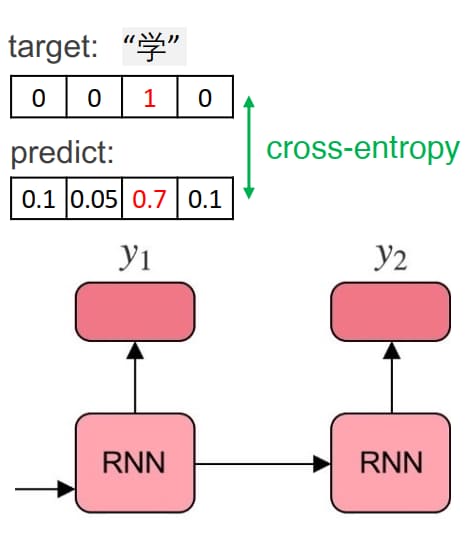
- 训练:
- 数据集 \(D=\{(x^(1),y^(1)),\dots,(x^(N),y^(N))\}\) 用于训练。
- 目标是通过优化交叉熵损失函数最小化预测概率与真实分布的差异。
- 损失函数:\(L(\theta \mid x, y) = – \sum_{i=1}^{T_y} \log p_\theta(y_i \mid y_{<i}, x)\) ,\(L(\theta \mid D) = \frac{1}{N} \sum_{n=1}^N L(\theta \mid x^{(n)}, y^{(n)})\) 。
- 优化:梯度下降。
- RNN 编解码器模型被广泛应用于翻译任务,并逐渐推广到其他领域,如自然语言处理(文本生成)和非自然语言领域(图像生成等)。然而,在处理长序列时,该模型存在显著问题:
- 模型瓶颈:
- RNN 编解码器将整个输入序列压缩为一个固定大小的上下文向量 c,用于表示整个序列,长序列在压缩过程中可能会丢失大量信息,导致对长文本的理解和生成能力较差。
- 性能随着序列长度的增长而显著下降。
- 固定上下文向量的局限:
- 编码器输出的上下文向量 cc 是整个序列的单一表示,无法动态关注序列中重要的部分。
- 无论序列中某些位置的重要性如何,所有信息都被等同对待,这进一步加剧了长序列处理的困难。
10.2. 注意力机制(Attetion)
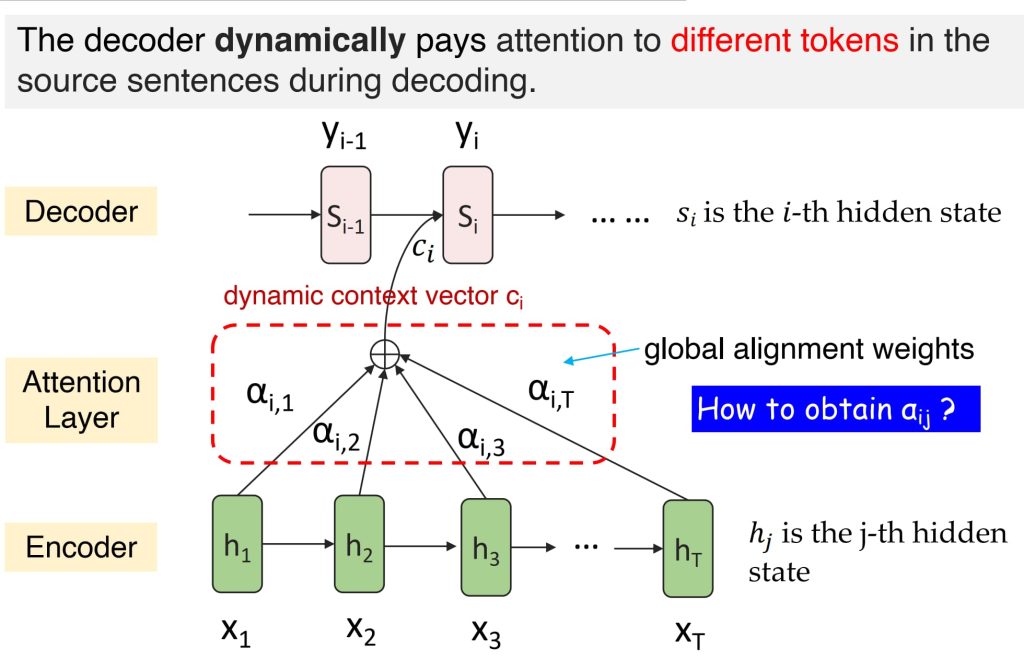
为了缓解长序列处理中的信息丢失问题,可以采用动态上下文向量(dynamic context vectors)的方法:
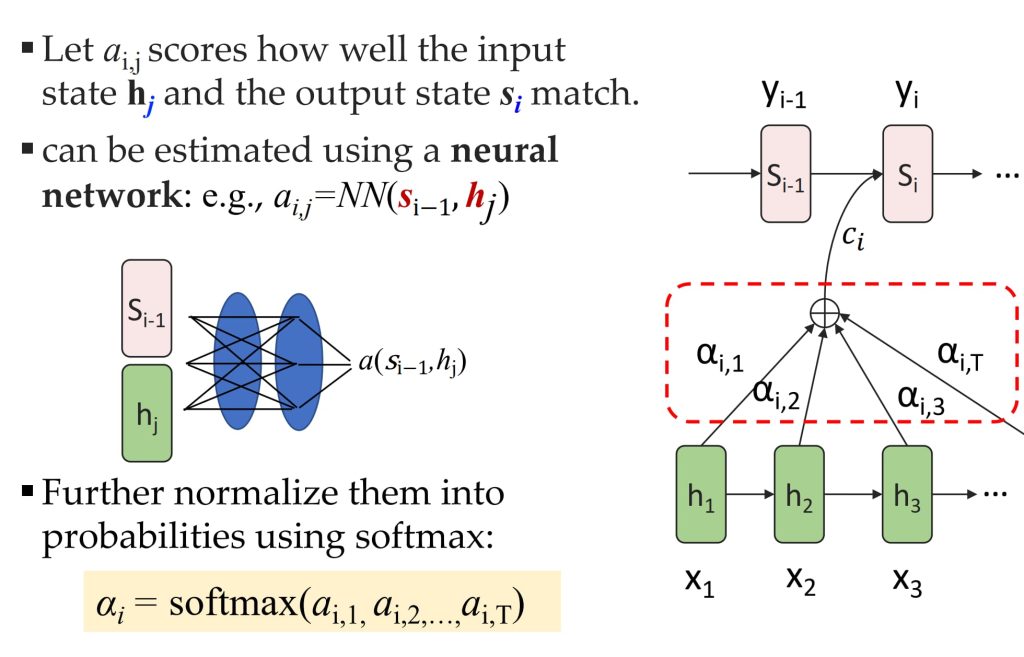
- 在解码每个目标序列的 \(y_i\) 时,使用动态上下文向量 \(c_i\)。
- \(c_i\) 是输入序列中隐藏状态的加权线性组合,权重由注意力机制决定。
- 计算公式:\(c_i = \sum_{j=1}^N a_{ij} h_j \quad s_i = \text{RNN}_\text{out}(y_{i-1}, s_{i-1}, c_i)\)
- 其中:\(h_j\): 输入序列中第 j 个位置的 Encoder 中的隐藏状态,\(a_{ij}\):第 i 个目标序列位置对第 j 个输入序列位置的注意力权重。
10.3. Transformer(seq2seq model with “Self-attention”)
- RNN 的局限性:
- 串行计算,效率较低:循环神经网络(RNN)由于其循环架构,在处理序列数据时需要严格按照时间步(time step)进行串行计算,无法实现并行处理。这种计算方式导致其效率较低,尤其是在处理较长序列时,计算成本和时间开销会显著增加。
- 长距离依赖问题:RNN 通过维护一个隐藏状态,依次将之前的单词与当前正在处理的单词结合起来。然而,这种串行计算方式对长距离依赖的捕获能力较弱,容易出现梯度消失或梯度爆炸的问题,从而影响模型性能。
- Self-Attention 的优势:
- 并行计算与高效处理:自注意力机制(Self-Attention)通过同时关注序列中所有相关单词,将其他词语的信息嵌入到当前正在处理的词语中。由于支持并行计算,它显著提升了模型的处理效率,尤其是在处理长序列时具有优势。
- 动态权重调整与长距离依赖捕获:自注意力机制能够动态调整每个词的重要性权重,灵活地捕获序列中词与词之间的关系。这种特性使其能够有效处理长距离依赖问题,显著优于传统 RNN。
- Transformer 的核心优势:自注意力机制是 Transformer 等现代架构的核心组件,它通过改进模型的上下文理解能力,为复杂语言任务提供了更强的表现力和灵活性。
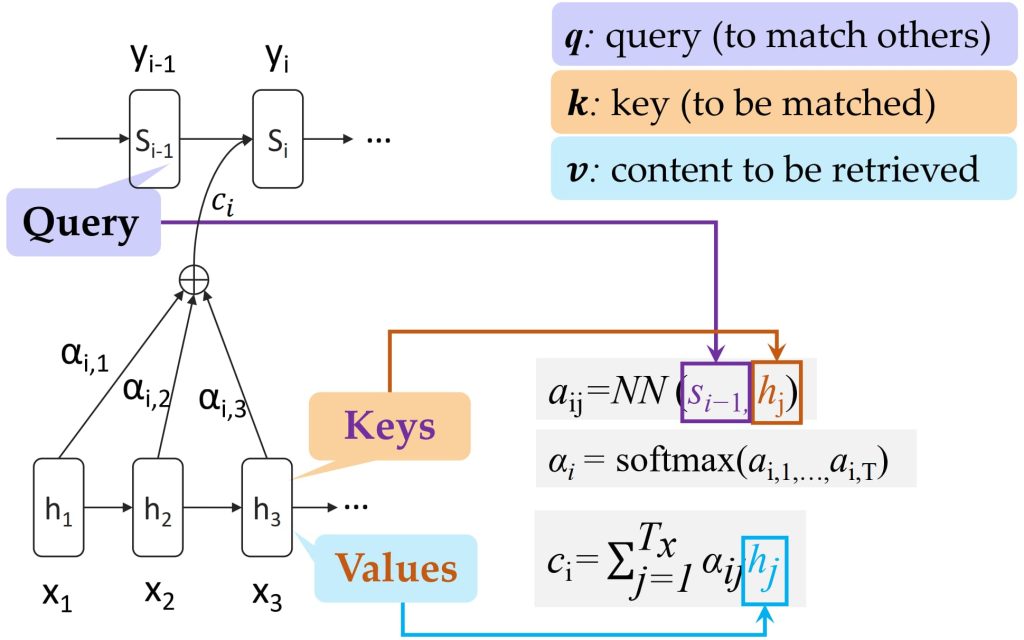
- Self-Attention 的核心思想:
- 每个词关注所有其他词:在自注意力机制中,每个词都会与序列中的所有其他词建立联系,关注它们之间的关系。
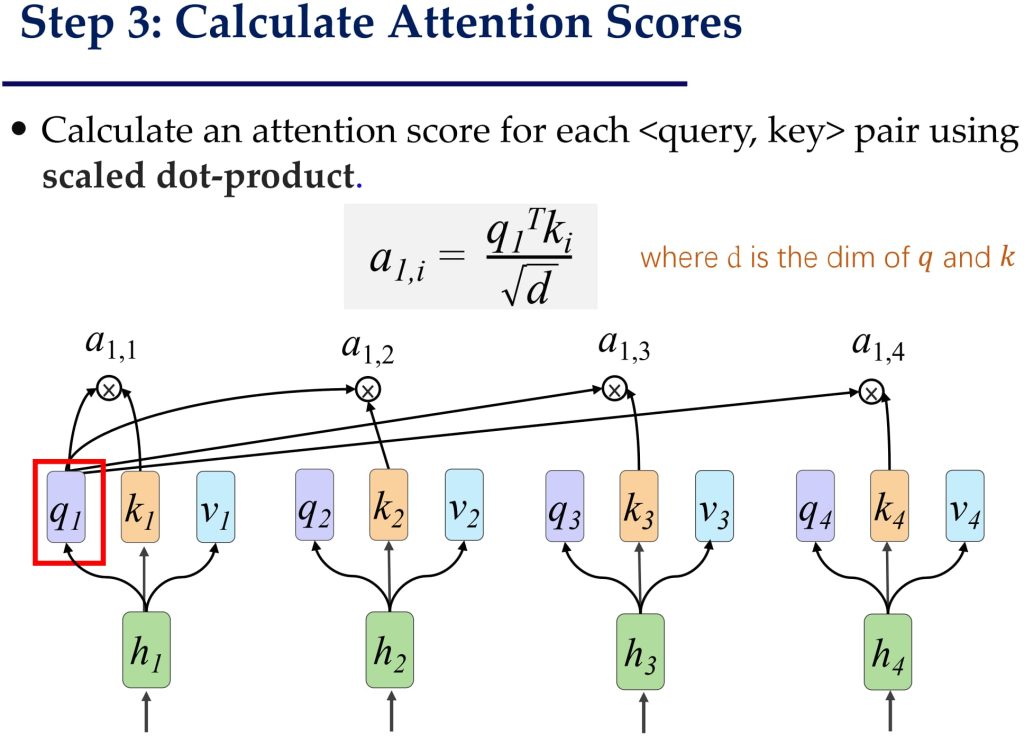
- 计算分数(Score):用查询向量(Query)与每个键向量(Key)进行点积运算(Dot Product),然后通过 Softmax 转化为分数(Score),以衡量当前词与其他词的相关性。
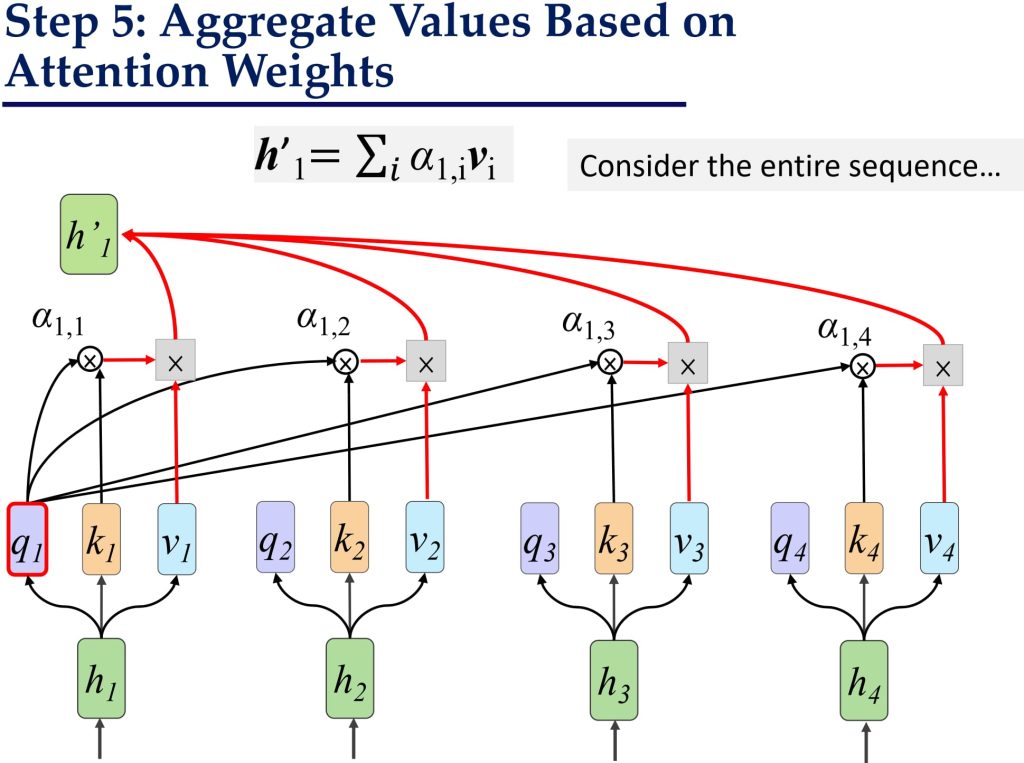
- 加权求和:将每个值向量(Value)乘以相应的分数(权重),然后对所有加权值向量求和,得到最终的输出向量。
- 输出表示新状态:得到的输出向量代表了查询词的新状态(即“更新后的记忆”),它综合考虑了与其他词的关系。
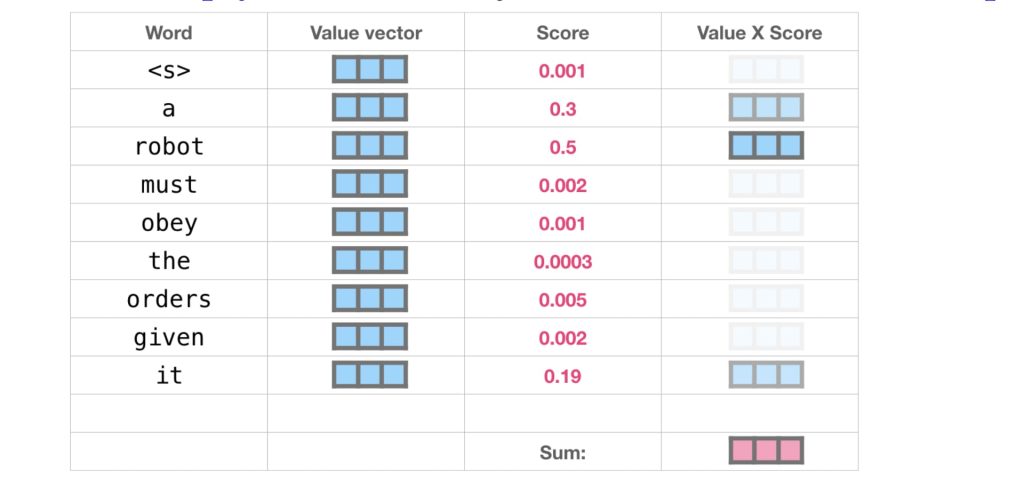
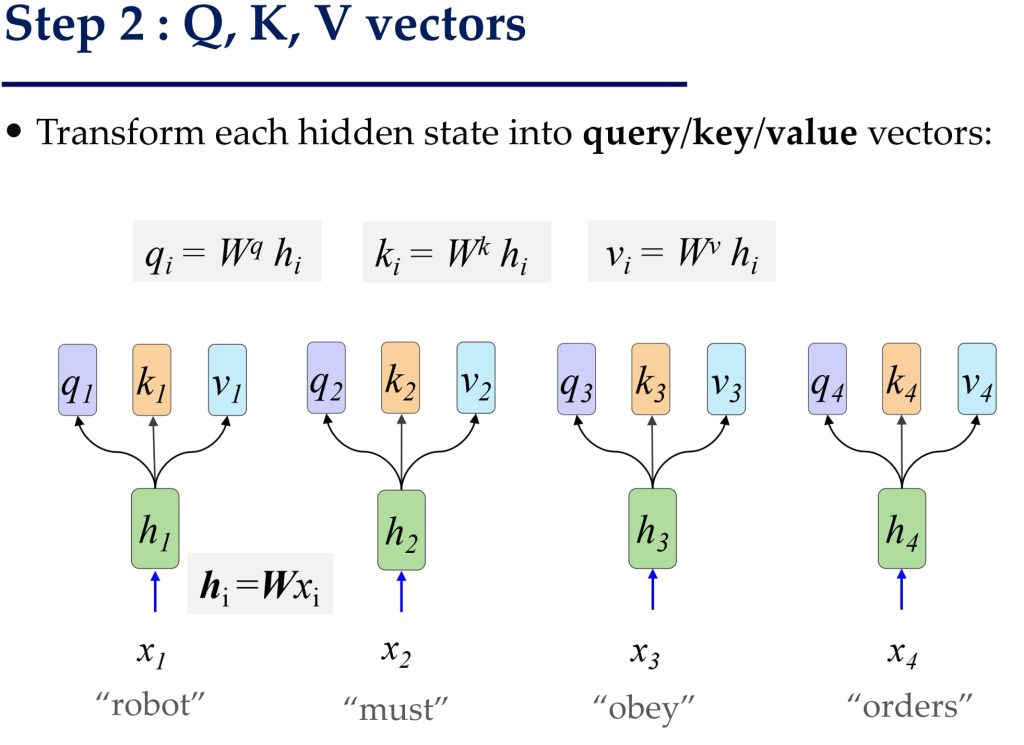
10.3.1. Self-Attention 过程步骤:
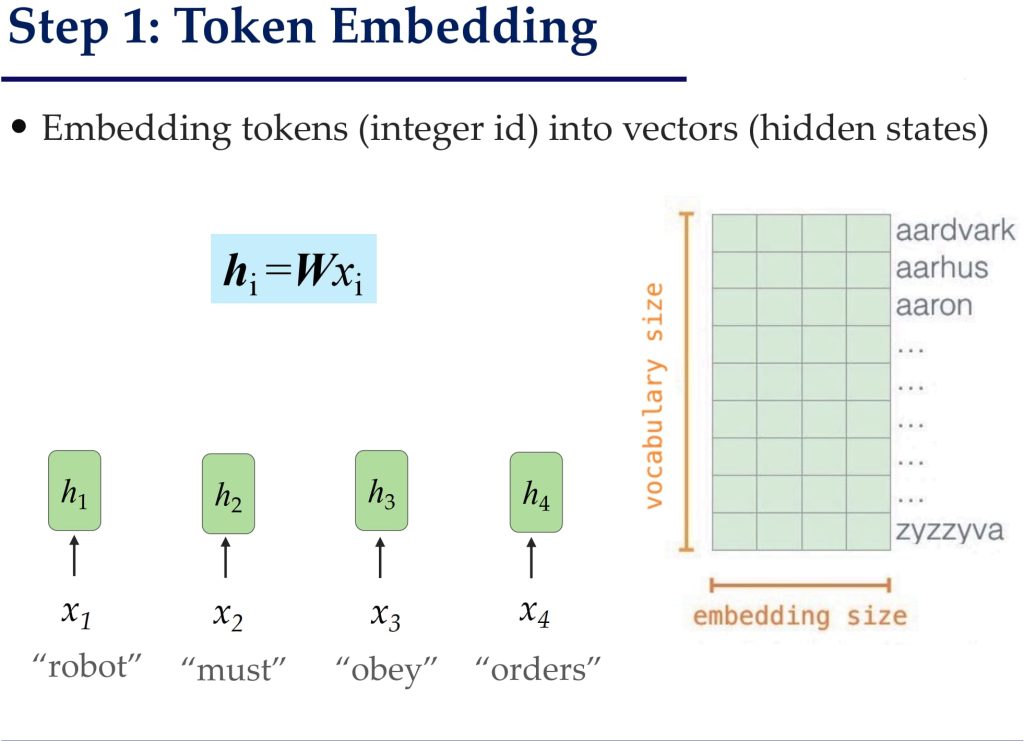
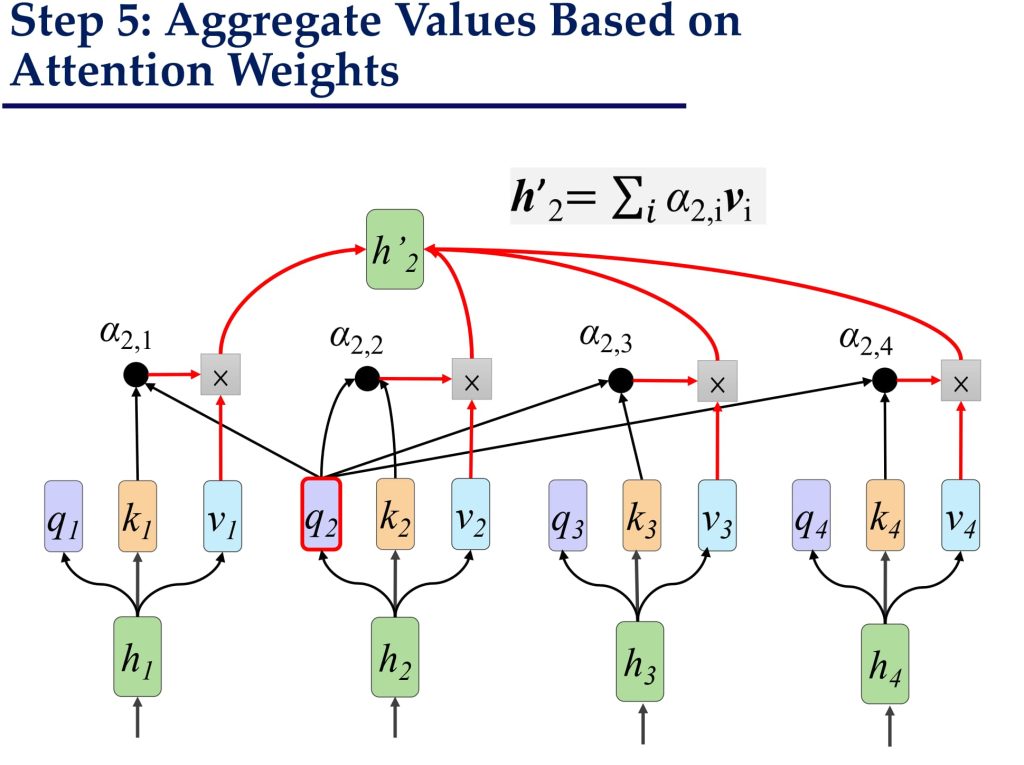
示例:
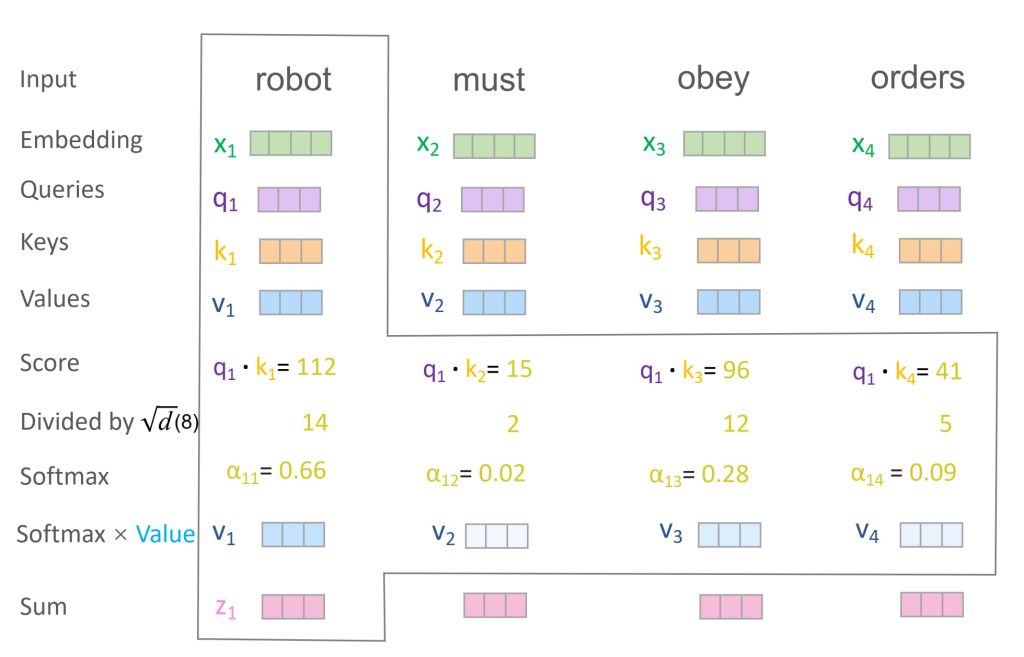

矩阵形式:
- 输入向量变换为 Query, Key 和 Value
- 每个输入词向量 \(h_i\) 通过线性变换得到对应的 Query (\(q_i = W^qh_i\))、Key (\(k_i = W^kh_i\)) 和 Value (\(v_i = W^vh_i\)):
- 将所有词的向量组合成矩阵形式:\(Q=W^qH, K=W^kH, V=W^vH\),其中 H 表示输入词向量矩阵。
- 计算注意力分数矩阵 A
- 注意力分数矩阵 AA 是通过 Query 和 Key 的点积计算的:\(A=\frac{K^TQ}{\sqrt{d}}\),其中,\(A_{i,j}\) 表示第 i 个词对第 j 个词的相关性。
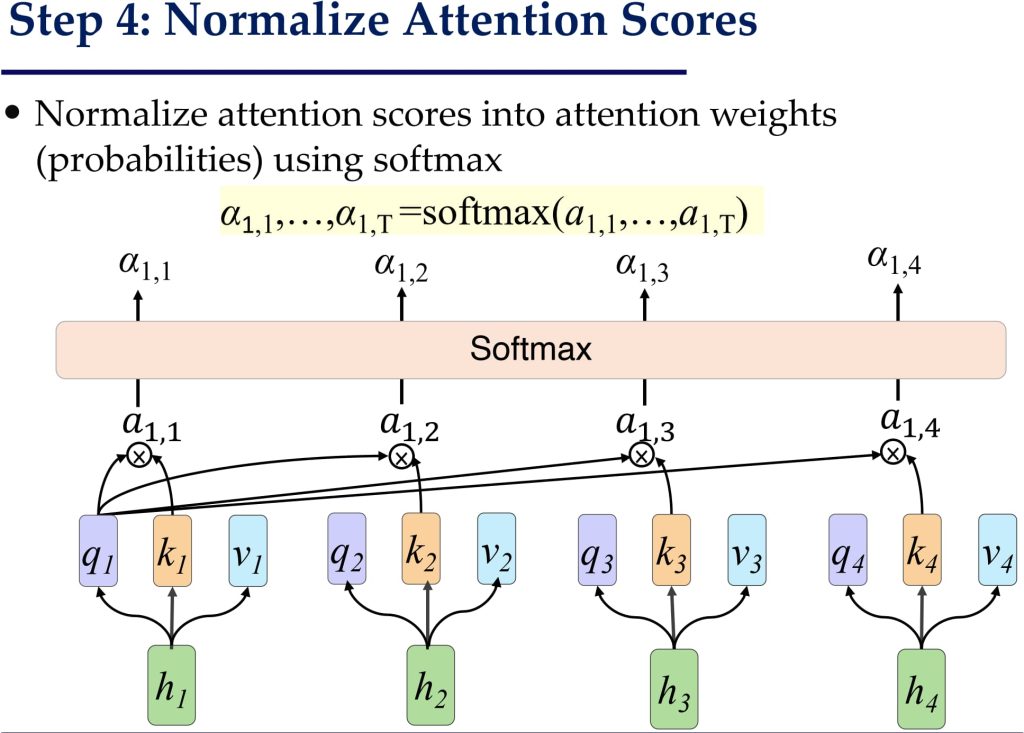
- 应用 Softmax 转化为权重矩阵 \(\hat{A}\)
- 对 AA 的每一行应用 Softmax 操作,将注意力分数归一化为概率分布:\(\hat{A}_{i,j} = \text{Softmax}(A_{i,j})\)
- 加权求和得到新的表示 H′
- 将权重矩阵 \(\hat{A}\) 与 Value 矩阵 V 相乘,得到最终的输出矩阵 H′:\(H’ = V\hat{A}\)
- 其中 \(h_i’=\sum_{j=1}^{n}\hat{A}_{i,j}v_j\) 表示第 i 个词的更新向量。
Self-Attention 如何表示顺序:
- 位置编码:每个位置都会被分配一个唯一的位置嵌入 \(e_i\)。
- 位置嵌入 \(e_i\) 会被加到词嵌入 \(h_i\) 上,作为自注意力层的输入。
- 假设 \(p_i\) 是一个表示序列中 \(x_i\) 位置的one-hot 向量,那么 \(e_i\) 可以通过一个可学习的嵌入矩阵 \(W_p\) 获得:\(e_i = W_p p_i\)
10.3.2. 完整的 Transformer 架构:
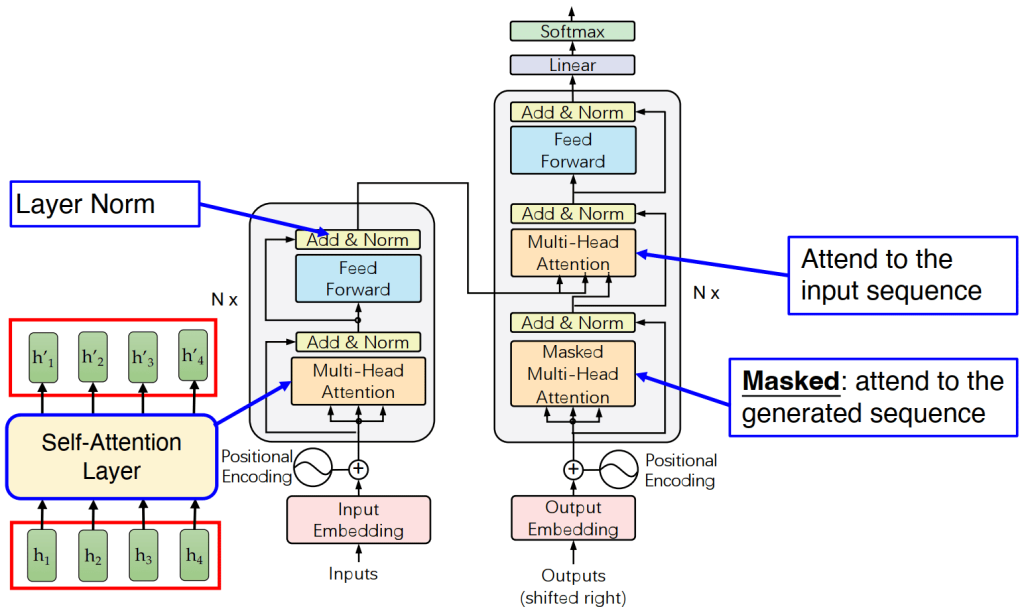
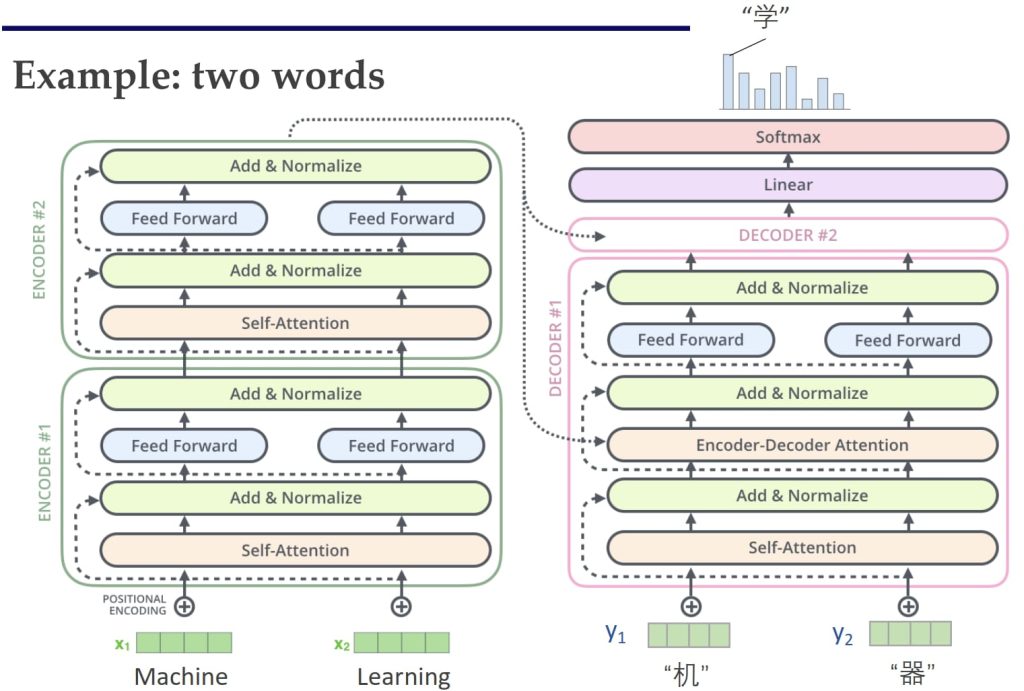
左侧的 Encoder 通过 Self-Attention 层对输入序列进行处理,生成新的上下文表示 H。右侧的 Decoder 接收来自 Encoder 的输出 H,将其转化为 Key (K) 和 Value (V),同时将自身的已生成序列理解为 Query (Q)。Decoder 中的 Multi-Head Attention 层实现了两两交叉的注意力机制:一个用于关注 Encoder 的输出序列(Encoder-Decoder Attention),另一个是 Masked Self-Attention,用于关注自身的已生成序列。最后,Decoder 的输出经过线性变换和 Softmax 分类层,生成最终的预测结果。
Decoder部分:
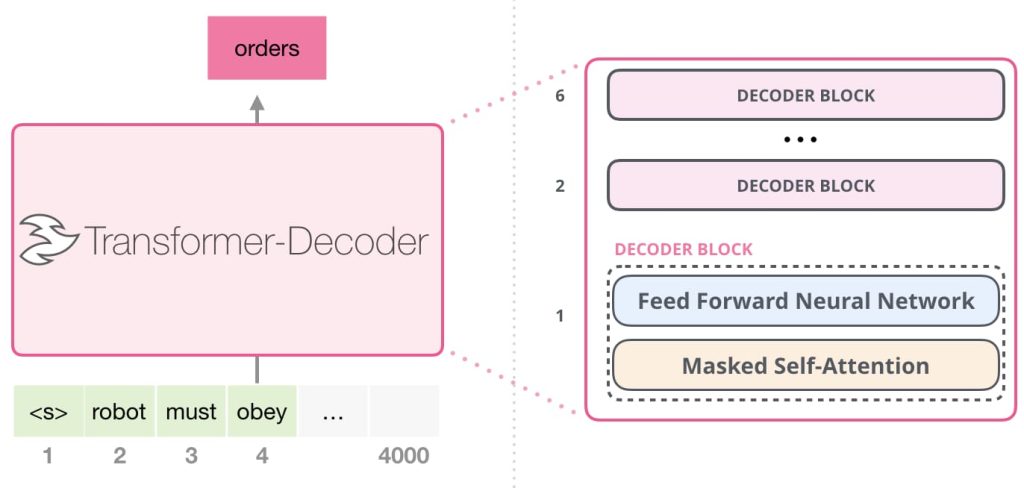
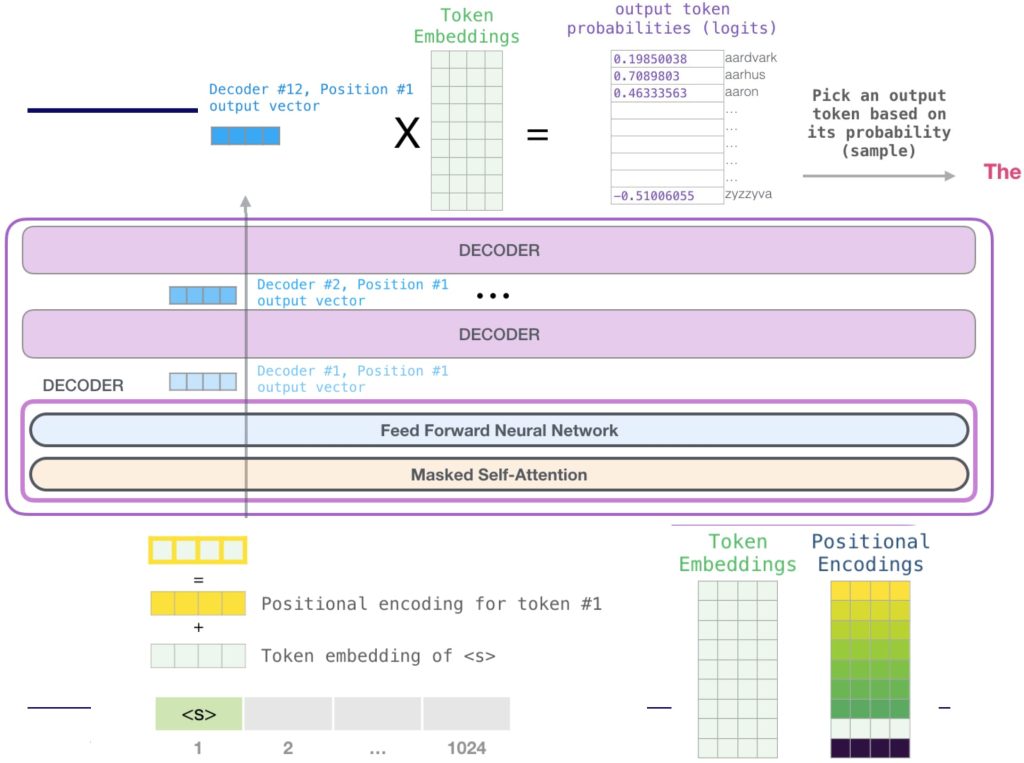
10.3.3. 注意力遮罩(Attetion Masks)
Attention Masks 是用于限制注意力机制中关注范围的矩阵,通过对注意力分数进行修正,避免模型关注到不必要或无效的 token。
- Self-Attention Mask
- 用于 Encoder 和 Decoder。
- 作用:忽略输入序列中的填充 token(padding tokens)。
- Cross-Attention Mask
- 仅用于 Decoder,在处理 Encoder 的输出时。
- 作用:忽略源输入序列中的填充 token。
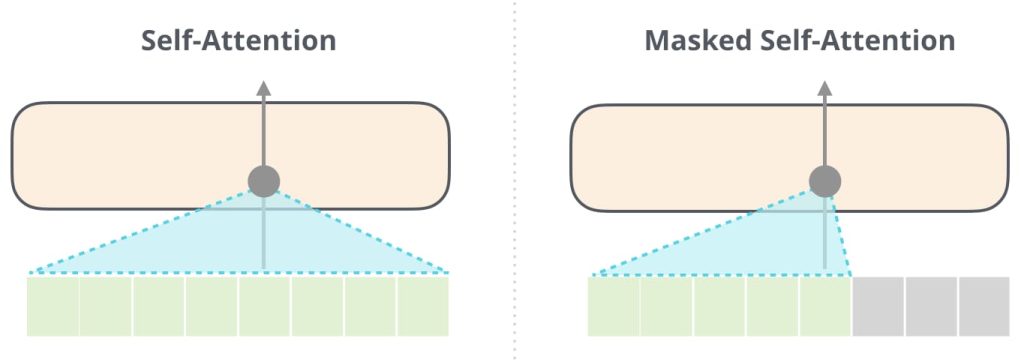
- Causal Mask
- 仅用于 Decoder。
- 作用:确保模型只关注已生成的 token,避免未来信息泄漏(即因果性约束)。


10.3.4.训练
与 RNN Encoder-Decoder 相同。
11. 大语言模型(Large Language Model)
11.1. 预训练语言模型(Pre-trained Language Models)
预训练语言模型的训练和使用分为两个阶段,这种两阶段训练方式有效结合了无监督学习和监督学习的优势,成为现代 NLP 的主流方法:
- Pre-Training(预训练)
- 目标:学习通用的语言表示。
- 方法:在大规模无标注的文本数据上进行无监督训练;典型数据来源:书籍、维基百科等;常用任务:语言建模、掩码语言建模(如 BERT 的 Masked Language Modeling,MLM)。
- 结果:模型掌握了语言结构、语义关系等知识,具备通用的语言理解能力。
- Fine-Tuning(微调)
- 目标:解决特定的下游任务(如垃圾邮件检测、情感分析等)。
- 方法:在带标注的小规模任务数据集上进行监督训练;通过调整预训练模型的参数,使其适应特定任务。
- 优势:利用预训练中学到的丰富语言知识,微调所需数据量较少;微调后的模型表现优异,能够适应多种任务。
11.2. BERT(Bidirectional Encoder Representation from Transformers)
- 双向性:
- BERT 使用双向 Transformer 编码器,能够同时考虑上下文中的前后信息。
- 相比单向模型(如左到右的语言模型),双向机制使 BERT 对语言理解更加深刻。
- 输入格式:
- 输入是一系列单词(或词片段)。
- 特殊标记 [CLS]:作为第一个输入标记,用于分类任务的最终输出。
- 特殊标记 [SEP]:用于分隔两个句子(在句子对任务中)。
- 预训练方式:
- Masked Language Model (MLM):通过随机掩盖输入 tokens(15%),Encoder 连接分类器,学习预测被掩盖的 token,帮助模型学习通过上下文预测词语。
- Next Sentence Prediction (NSP):通过分隔两个句子,Encoder 连接分类器,学习预测两个句子在语义上连接的可能性,帮助模型学习理解句子间的语义关系和上下文逻辑。
- 微调应用:
- 句子分类:输入:单个句子;输出:句子的分类。例如:情感分析,文档分类。
- 词语标记:输入:单个句子;输出:每个单词的分类。例如:槽填充。
- 语句对关系预测:输入:两个句子;输出:关系。例如:自然语言推理。
- QA(阅读理解):输入:一系列文档和问题;输出:答案起始位置在文档中的标记。
11.3. GPT(Generative Pre-Trained Transformer)
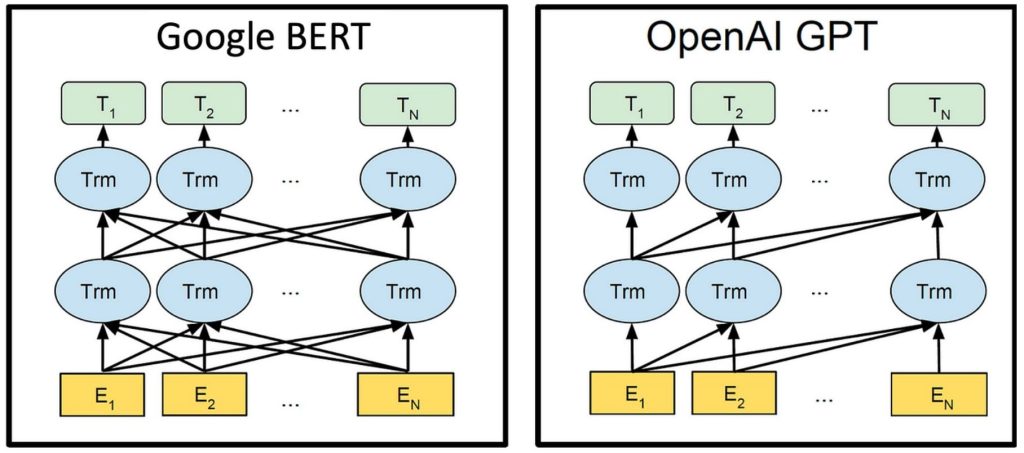
- BERT:
- 基于Transformer的双向编码器架构,通过同时从左到右和从右到左读取输入文本(双向上下文),可以更好地捕捉句子中的上下文信息。
- 主要采用 MLM 和 NSP 作为预训练任务,适合于理解任务。
- 主要用于自然语言理解(NLU)任务。
- GPT:
- 基于Transformer的单向解码器架构,采用从左到右的方式生成文本(单向上下文),适合生成任务。
- 目标是给定前文,预测下一个词,专注于生成任务。
- 主要用于自然语言生成(NLG)任务。
预训练 GPT:简单的语言模型:给定前 n – 1 个 tokens,预测第 n 个 token。
训练目标:\(l(\theta)=-\sum_{t=1}^{T} \log p_{\theta} (x_t \mid x_1,\dots,x_{t-1})\)
11.4. Utilize LLMs
- 微调(Fine-tuning)
- Full fine-tuning:计算复杂,容易过拟合;
- Parameter-Efficient Fine-Tuning(PEFT):效率高,资源节约,使用任务场景灵活
- Prompt Tuning:在原始输入前添加可学习的伪token(提示),仅优化这些伪token的嵌入表示。
- Low-Rank Adaptation,LoRA:通过低秩矩阵分解对模型权重更新进行表示。
- 涌现(Emergent):涌现能力指随着大规模语言模型(LLM)规模增加,突然出现的全新行为。这种能力表现为模型无需特定任务训练,仅通过自然语言描述即可完成任务,能力增长呈高度非线性。
- 提示工程(Prompting):任务描述的提示
- Few-Shot:少量演示例子的提示。
- Chain-of-Thought:通过逐步推理的方式,引导模型一步步解决问题。
- 检索增强生成(Retrieval-Augmented Generation,RAG):
- 核心组件:
- 嵌入模型:将输入文本转化为嵌入向量,便于快速检索。
- 向量数据库:存储知识及其对应的嵌入向量。
- LLM:基于检索到的知识生成响应。
- 工作流程:
- 索引阶段:将文档分块并嵌入为向量,方便后续检索。
- 检索阶段:根据用户查询生成查询向量,与数据库中的向量比较,找到最相关的前K个文档块。
- 生成阶段:将检索到的文档块与原始提示结合,输入 LLM 生成最终响应。
- 核心组件:
12. 卷积神经网络(Convolutional Neural Networks,CNN)
12.1. 机器如何理解图片?
- 如果将像素矩阵作为输入给分类器:过于敏感,图片稍微旋转或者其他效果变化(光照、遮挡、形变或背景干扰),都会导致输出变化,且很难关注图片周围的上下文和类内差异。
- 手动提取图片特征:需要大量的人工标注。
- 深度学习 MLP:
- 破坏图像空间结构:将图像视为像素序列会破坏其固有的二维空间结构(如局部纹理、形状关系)。
- 局部不敏感性:模型关注整体图像而非局部特征(例如无法有效识别边缘、角落等局部模式)。
- 平移敏感性:对特征的全局位置敏感(同一特征在不同位置会被视为不同特征,缺乏平移不变性)。
- 参数量过大:全连接层(Fully Connected Layers)导致参数量激增(例如输入为1000×1000图像时,单层参数可达10^9量级)。
- 设计目标:
- 保持空间结构(保留图像的二维几何关系,如相邻像素的拓扑连接性)
- 局部敏感性(强调模型对局部特征的响应能力,如边缘、纹理等)
- 处理输入图像的变体(适应图像的变化,如平移、旋转、光照差异等)
- 跨空间区域的参数共享(例如卷积核在图像不同位置复用参数,降低计算量)
12.2. 从 MLP 到 CNN
- 卷积的核心思想:
- 输入为二维图像:图像由像素值组成,可以通过扫描来检测特定特征。
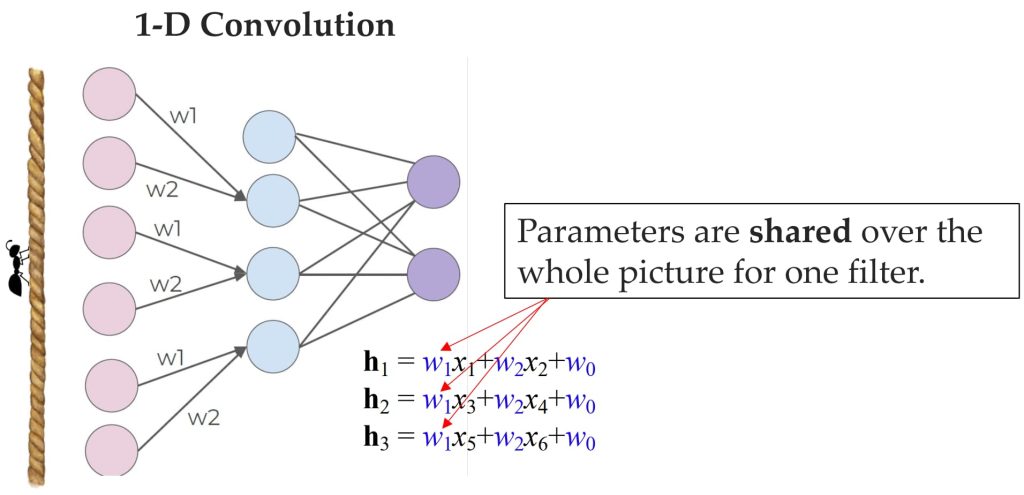
- 局部连接:将输入层的局部区域(图像中的一个小块)连接到后续层的单一神经元,用于特征提取。
- 滑动窗口操作:通过在图像上滑动窗口(局部区域),逐步计算特征变换。
- 权重共享:滑动过程中,所有神经元的权重必须共享,目的是减少参数数量,提高模型效率,并确保在不同位置检测相同特征。
- 重新设计 MLP:
- 限制隐藏单元的范围以关注局部特征:通过让每个隐藏单元只连接到输入单元的局部区域,可以更好地捕捉局部特征,而不是处理整个输入范围。
- 隐藏单元之间共享权重:通过共享权重,减少模型参数数量,同时增强模型的泛化能力。
12.3. 卷积和滤波器(Convolutions and Filters)
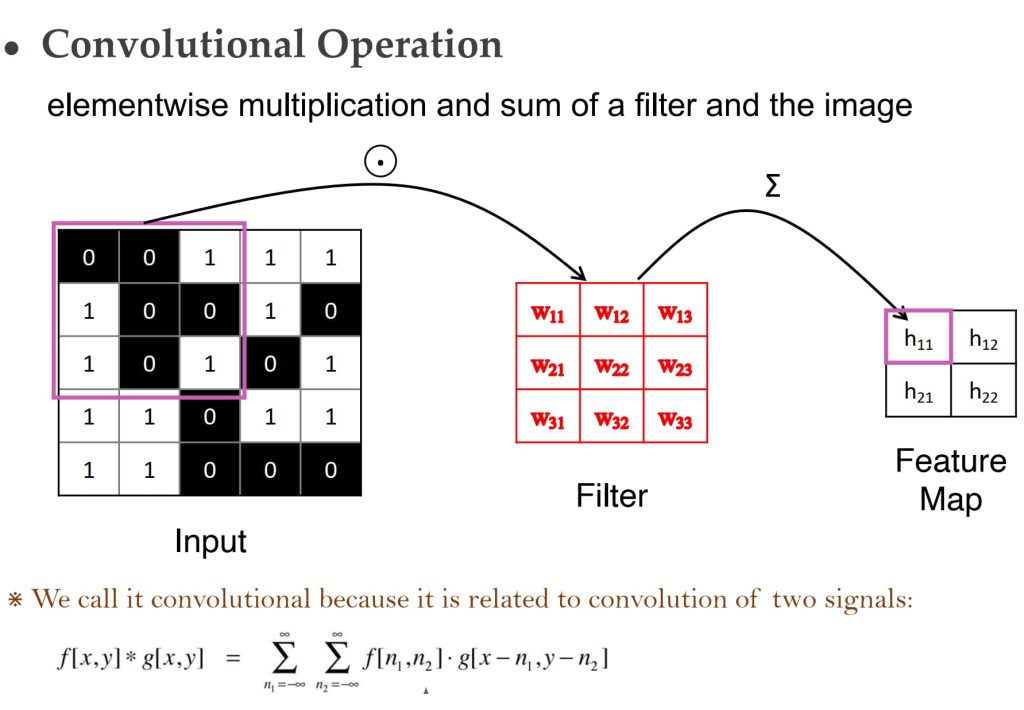
- 卷积核(Filter):卷积核是一个小的权重矩阵,用于对输入区域进行加权计算。它可以看作是一个检测局部特征的工具。
- 参数共享:一个卷积核的权重在整个输入数据中共享,这意味着它会对每个局部区域执行相同的计算。这种方式可以有效减少参数数量,提高计算效率。
- 滑动窗口操作:卷积核会在输入数据上滑动,逐步计算每个局部区域的特征值。
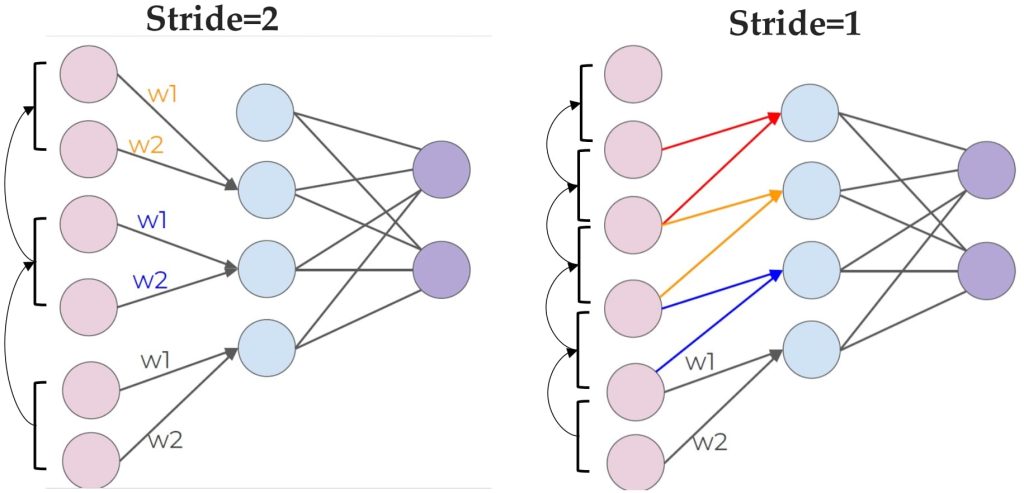
- 步长(Stride):步长决定了卷积核每次滑动时移动的距离。
- 多滤波器(Multiple Filters):可以使用多个卷积核,每个卷积核负责检测不同的特征。这使得模型能够捕捉数据中的多样性信息。
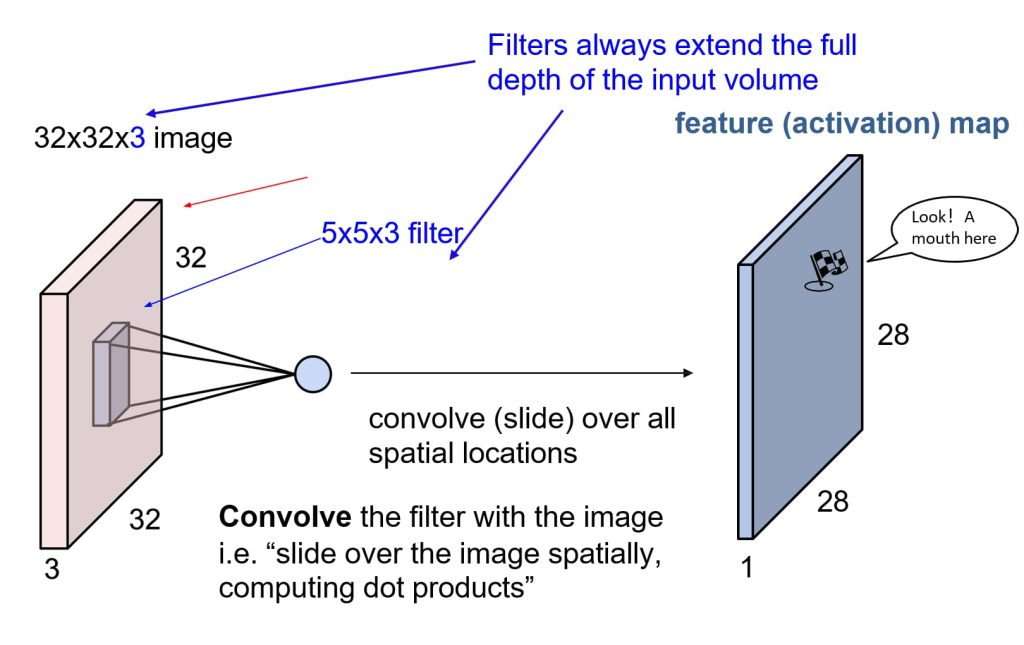
- 三维卷积的基本概念
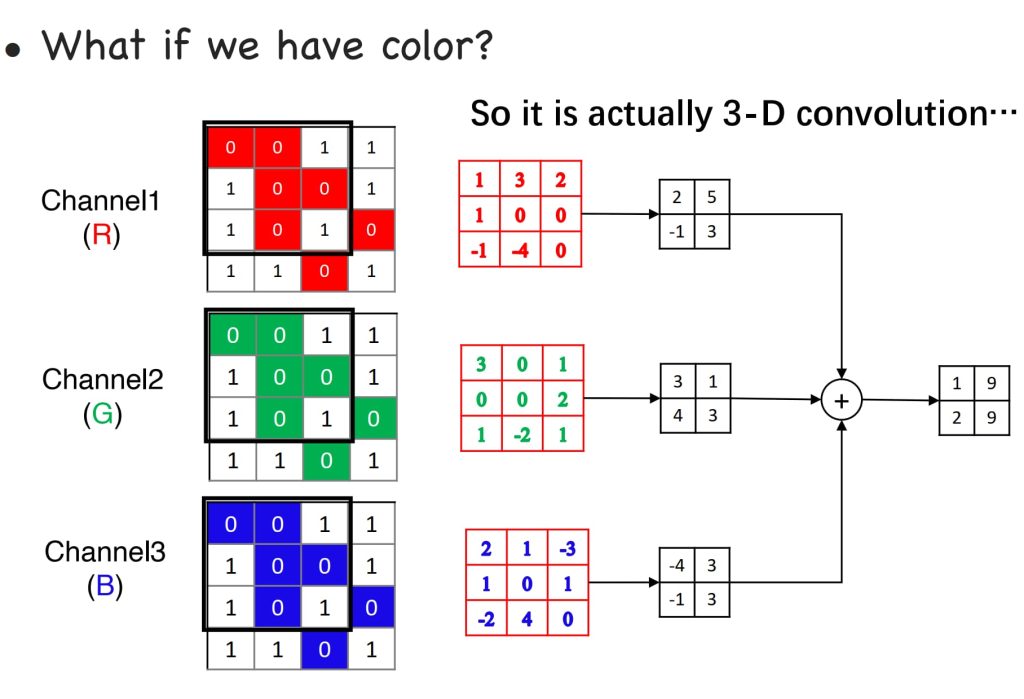
- 输入数据:三维卷积处理的是带有多个通道的输入数据(例如彩色图像有3个通道:RGB)。
- 卷积核(Filter):卷积核的深度与输入数据的通道数相同(例如,5×5×3的卷积核用于32×32×3的输入图像)。
- 操作:卷积核在空间维度上滑动(例如在32×32像素区域内滑动),计算点积以提取特征。
- 特征图(Feature Map)
- 定义:特征图是卷积操作后生成的结果,表示特定滤波器激活的区域。
- 过程:通过卷积核对输入数据的所有空间位置进行滑动,生成一个二维特征图。
- 尺寸变化:特征图的尺寸取决于卷积核大小、步长(stride)、以及输入数据的尺寸。
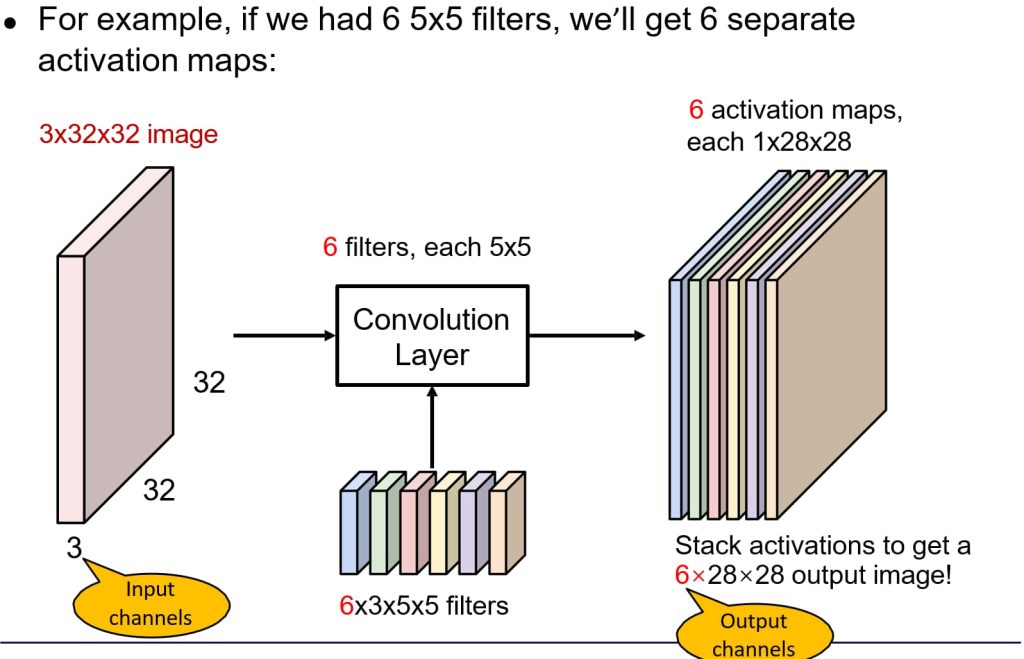
- 多滤波器(Multiple Filters)
- 多滤波器的作用:使用多个卷积核可以检测数据中的不同特征。
- 生成多个特征图:每个卷积核对应一个特征图。例如,6个5×5×3的卷积核会生成6个28×28的特征图。
- 输出通道:多个特征图会堆叠起来形成新的输出数据,作为下一层的输入。
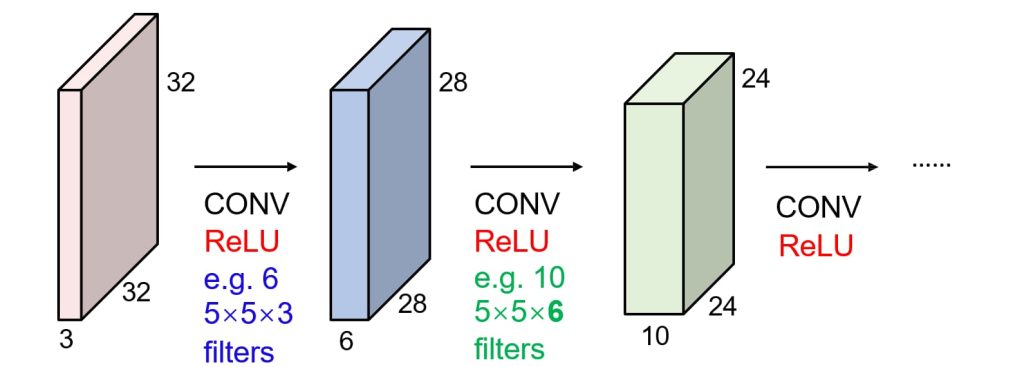
- 多层卷积(Multiple Layers)
- 层叠结构:多个卷积层依次堆叠,每层后通常跟随激活函数(例如ReLU),以增加非线性表达能力。
- 逐层学习:
- 第一层通常学习局部边缘、纹理等简单特征。
- 随着层数加深,模型能够学习更复杂、更抽象的特征(例如物体形状、类别等)。
- 特征图的变化:每层卷积操作后,特征图的数量增加,但空间尺寸可能减小。
- 卷积滤波器学习内容
- 低层滤波器:通常学习局部图像模板,例如边缘、颜色对比等。
- 高层滤波器:学习更加复杂的模式,例如物体的局部结构、整体形状等。
- 深层网络中的角色
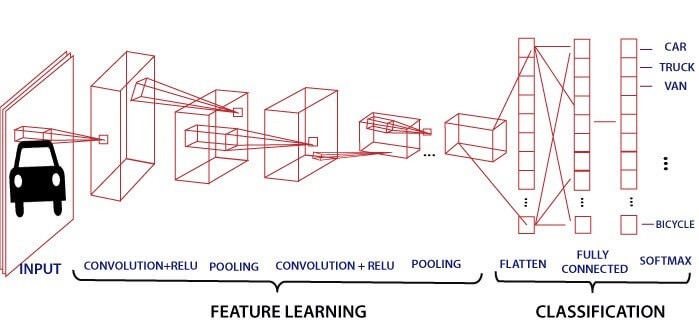
- 卷积层(CONV):提取特征。
- 激活层(ReLU):引入非线性。
- 池化层(POOL):降低特征图的尺寸,保留主要信息。
- 全连接层(FC):将提取的高层特征用于分类或回归任务。
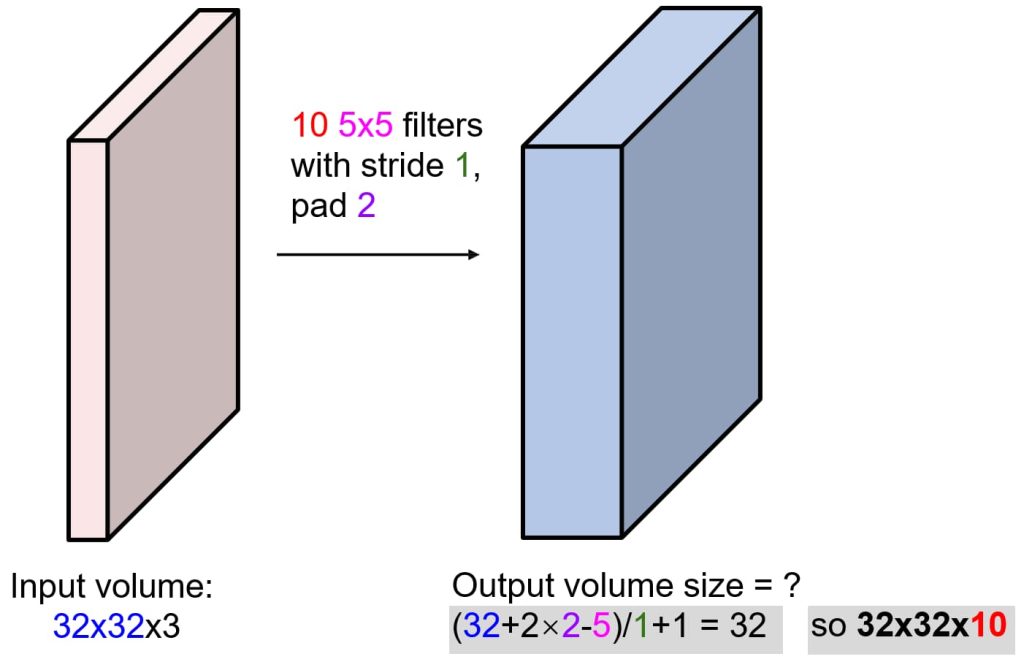
- 输入输出计算方式:output = (N + 2 * Padding – F) / stride + 1(N 输入图像尺寸,F 卷积核尺度)。
- 填充(Padding)
- 问题:卷积操作时,边缘像素可能无法完全被卷积核覆盖。
- 解决方法:
- Zero-Padding(零填充):在图像的边缘对称地添加零值,保留边缘信息,调整输入尺寸,使输出尺寸符合需求。
- Replication Padding(复制填充):复制边界像素进行填充;简单且常用,适合边缘特征较重要的任务;可能导致边缘特征过度重复。
- Reflective Padding(反射填充):镜像边缘的像素来填充;边缘的填充值更加符合实际的图像特征,减少零填充带来的不自然效果;对于某些任务可能引入过多的边缘信息。
- Constant Padding(常数填充):使用一个固定的常数值进行填充;可以根据任务需求灵活设置填充值。
- Circular Padding(循环填充):使用输入矩阵的元素进行循环填充;在某些周期性数据(如时间序列或循环图像)中非常有用。
- 优点:控制输出特征图的大小,有助于避免特征图尺寸随层数减小过快。
- 池化(Pooling)
- 目的:对特征图进行降采样,减少内存使用;使特征图更小、更易处理。
- 类型:
- Max Pooling:选择池化窗口中像素的最大值,保留图像的亮度特征或显著特征。
- Mean Pooling:选择池化窗口中像素的平均值,平滑图像,但可能丢失一些尖锐特征。
- 特点:没有可学习参数,引入空间不变性(Spatial Invariance),即对位置的轻微变化具有鲁棒性。
- 空间尺寸计算
- 公式:输出尺寸 = (输入尺寸 N + 2 * 填充 Padding – 滤波器尺寸 F) / 步长 stride + 1 。
- 池化计算:池化输出尺寸 = (输入尺寸 N – 池化窗口尺寸 F) / 步长 stride + 1
- CNN可以作为MLP吗?如何实现?
可以,通过将输入数据展平为一维向量并使用 1×11×1 卷积核,CNN能够模拟MLP的全连接层行为,同时保留其高效计算特点。 - CNN可以应用于文本吗?
可以,将文本转化为词向量或字符向量序列,用卷积核提取局部模式(如n-gram特征),并通过池化层总结信息,广泛用于文本分类、情感分析等任务。 - 为什么叠加太多卷积层效果反而变差?
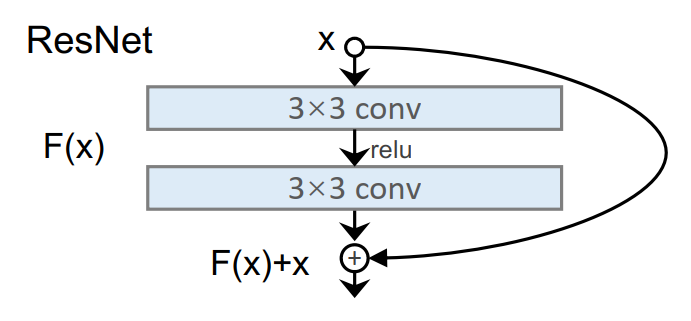
叠加过多卷积层可能导致信息丢失或漂移、梯度消失或优化困难,最终模型无法有效捕捉原始数据的关键特征。 - 残差网络(ResNet)如何解决上述问题?
残差网络通过引入跳跃连接,将原始输入直接传递到后续层,既保留了信息,又缓解了梯度消失问题,从而支持更深的网络结构。
13. 计算机视觉(Computer Vision)
- 计算机视觉任务:图片分类、图像分割、目标检测、图像描述生成、图像生成。
13.1. 图像分割(Image Segmentation)
- 直接对每个像素进行分类:图像中的像素数量非常多,逐个分类效率极低;单个像素缺乏空间信息,无法捕捉其上下文环境
- 通过滑动窗口 + CNN 分类图片块,分类图片块中央的像素:计算效率低下,因为每个窗口需要独立处理,计算成本非常高。
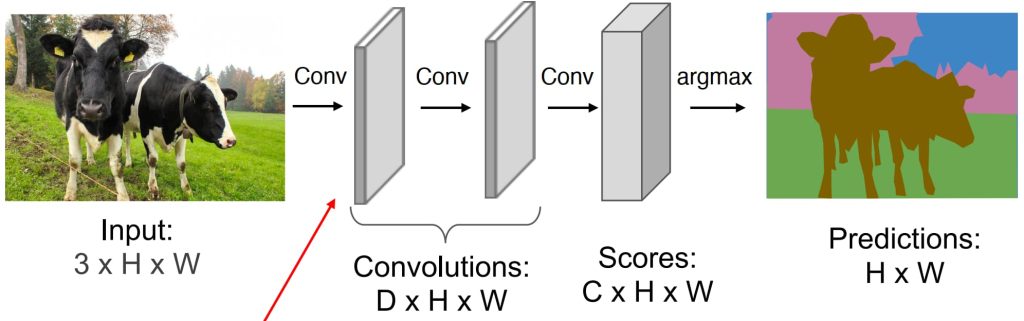
- Fully Convolutional Networks (FCNs):
- 基本思想:设计一个仅包含卷积层的网络,不使用下采样操作,直接对整个图像进行像素级预测。
- 可以一次性对所有像素进行预测,避免逐个处理;在原始图像分辨率上执行卷积操作计算量巨大,效率非常低。
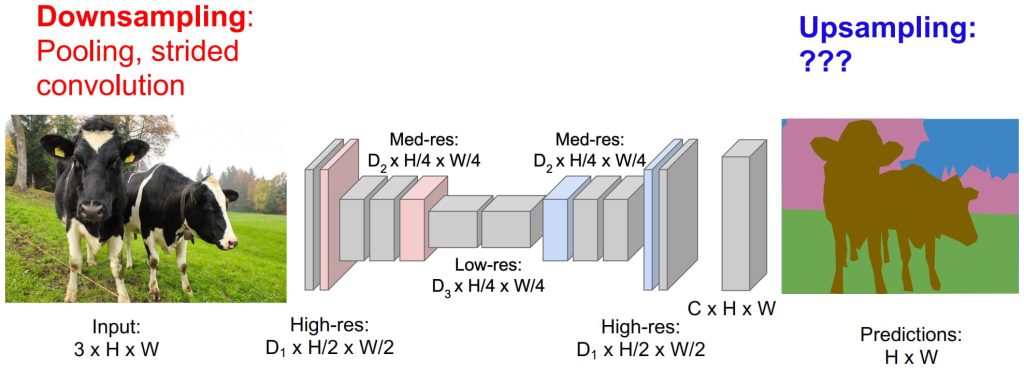
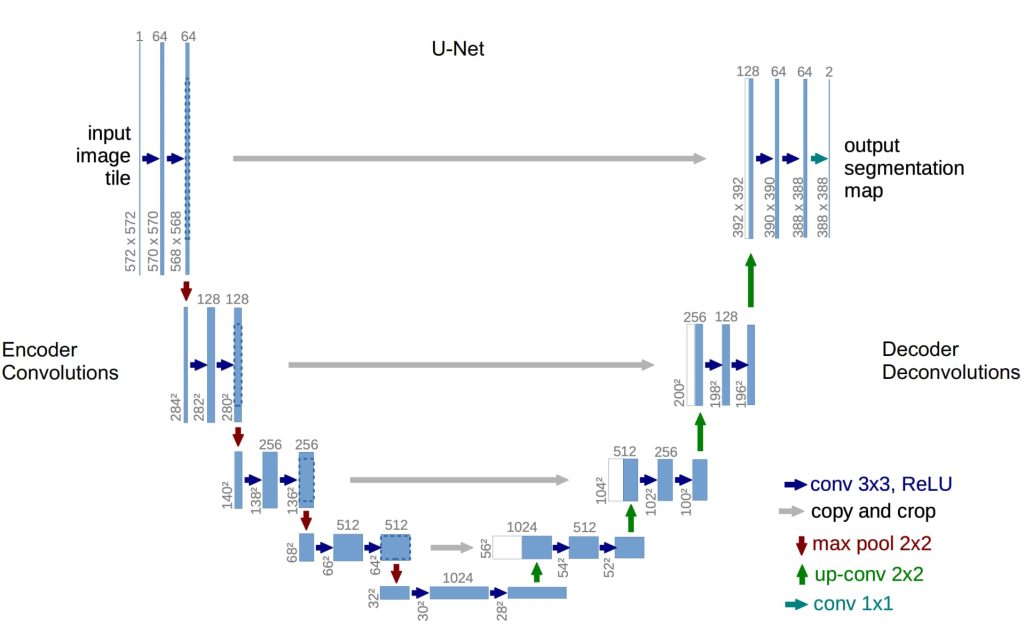
- 改进的 FCNs
- 更高效的方式:先在小图片上划出轮廓,再通过上采样操作复原成与原始图片大小相同的结果:
- 下采样:通过池化层或卷积层减少分辨率,提取高层次语义信息。
- 上采样:通过反卷积或插值恢复分辨率,实现像素级预测。
- 更高效的方式:先在小图片上划出轮廓,再通过上采样操作复原成与原始图片大小相同的结果:
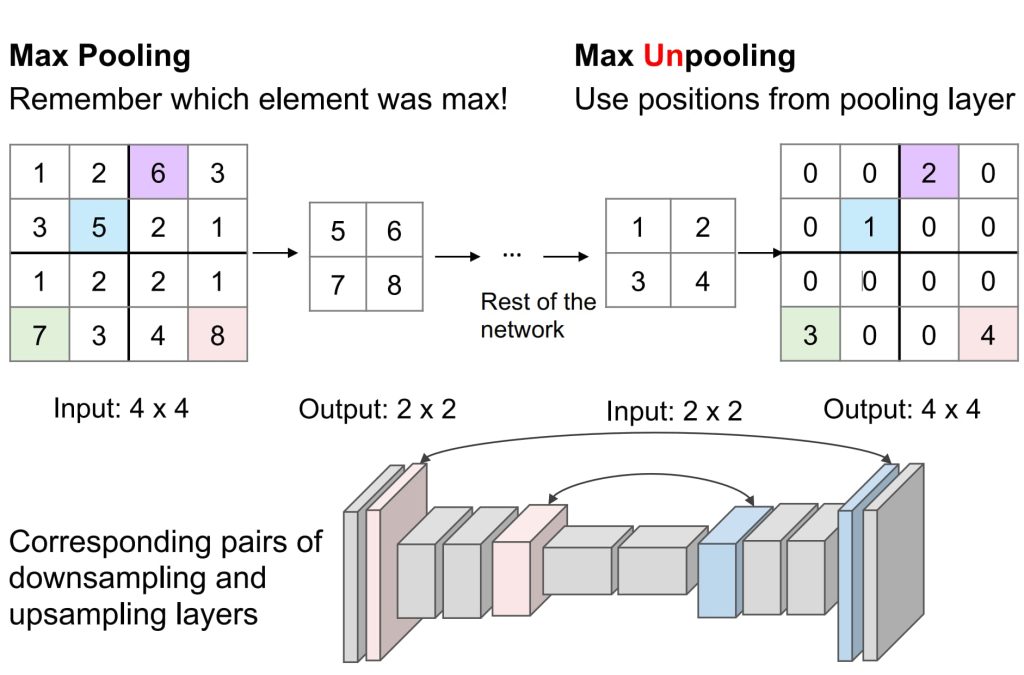
- 上采样,反池化(Unpooling)的方法:
- 最近邻插值(Nearest Neighbor):将输入的每个像素值复制到扩展的网格中。
- 钉床(Bed of Nails):将输入的像素值放置在输出矩阵的特定位置(通常是对应池化操作的位置),而其他位置全部填充为 0 。
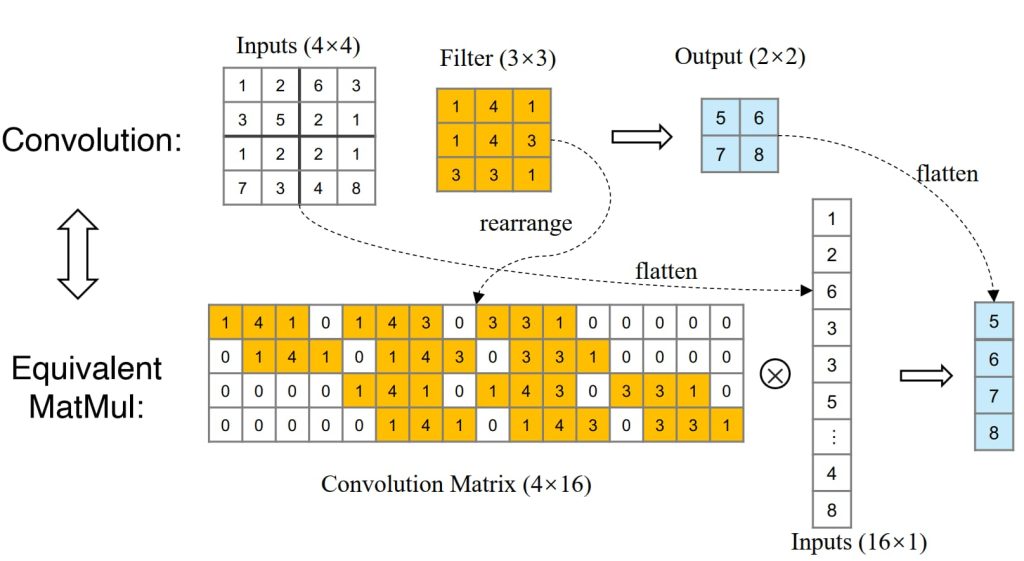
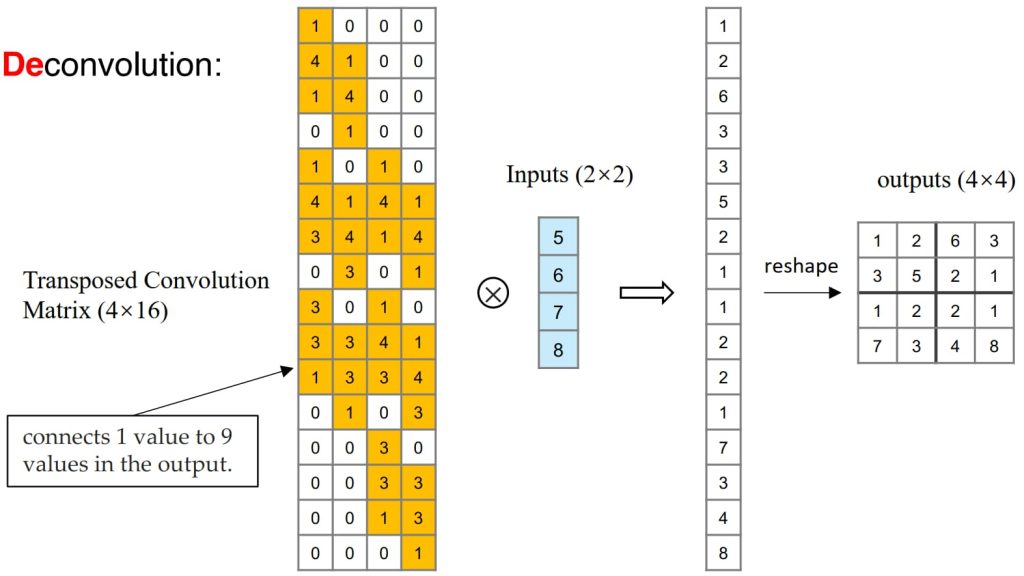
- 使用转置卷积进行上采样
- 可以通过将卷积核矩阵重新排列成一个通用矩阵的形式,将卷积操作重新表述为矩阵乘法;
- 将卷积矩阵 C(大小为 4×16)转置为 \(C^T\)(大小为 16×4)再与一个列向量(大小为 4×1)进行矩阵乘法,生成一个输出矩阵(大小为 16×1)。
13.2. 目标检测(Object Detection)
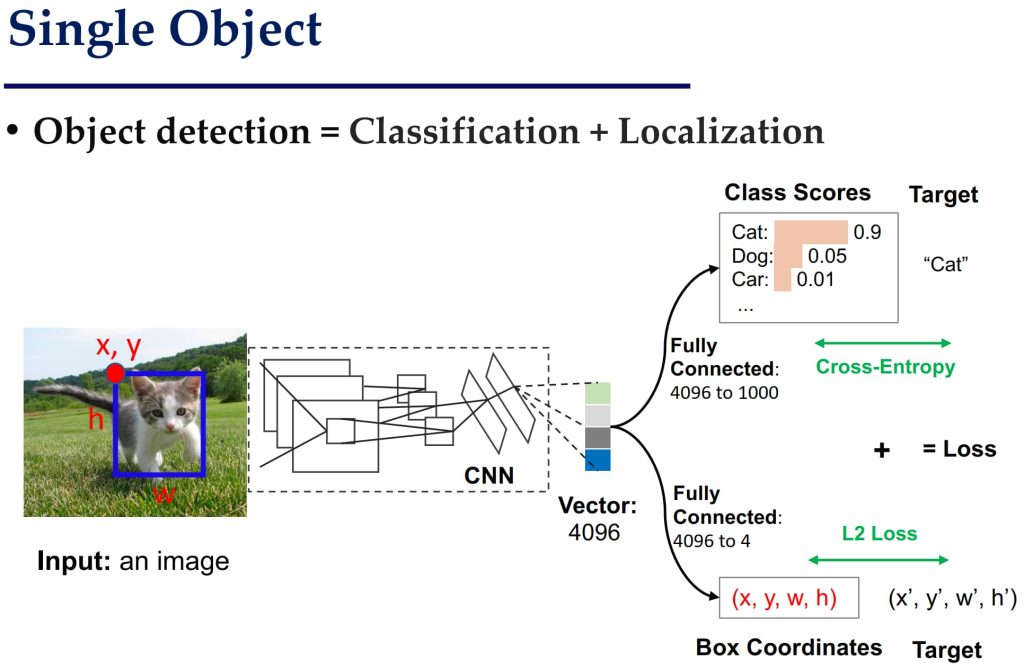
- 单对象检测:分类 (Classification): 确定图像中的目标属于哪一类(如猫、狗、车等);定位 (Localization): 确定目标的边界框 (Bounding Box),即目标所在的位置和大小 (x, y, w, h)。
- 多对象检测:每张图像可能包含不定数量的目标,每个目标需要独立的分类和定位输出
- 滑动窗口法:
- 枚举图像中的所有可能区域(使用滑动窗口),对每个区域应用 CNN,判断是否包含目标,并分类目标
- 每个窗口需要单独通过 CNN,计算量非常大;需要尝试多个窗口大小、比例和位置,导致效率低下。
- 区域建议 (Region Proposals):
- 通过某种算法快速生成可能包含目标的候选区域(即目标区域的候选框),对这些候选区域应用 CNN 进行分类和定位。
- Selective Search 是一种常见的区域建议方法:它通过图像的颜色、纹理、形状等信息找到 “块状” 区域,作为候选目标区域。优缺点:运行速度较快但生成区域数量仍较多。
- R-CNN (Region-based CNN)
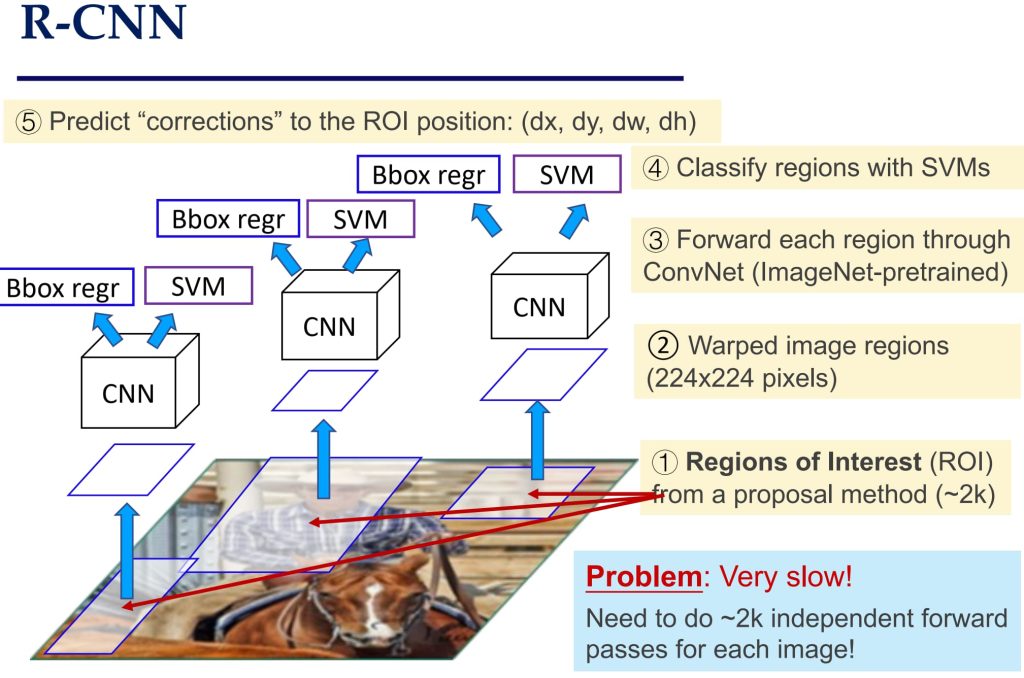
- 使用 Selective Search 生成候选区域,将每个候选区域变换为固定大小,单独输入 CNN 提取特征,使用 SVM 对每个区域进行分类,使用回归模型调整边界框的位置。
- 非常慢,每张图像需要对所有候选区域单独进行 CNN 前向传播,计算量巨大;需要单独训练分类器(SVM)和边界框回归器,训练复杂。
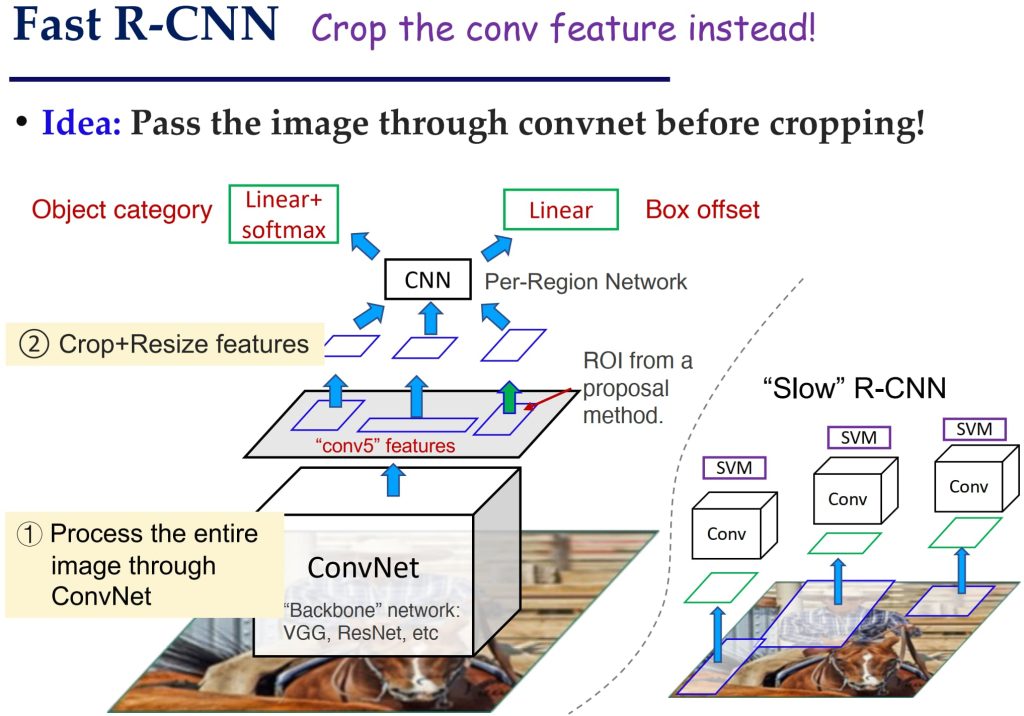
- Fast R-CNN
- 先处理整张图像:直接将整个图像输入 CNN 提取特征;ROI Pooling:对候选区域在特征图上进行裁剪和池化,避免重复计算 CNN;统一网络:分类和边界框回归在同一个网络中完成。
- 整张图像只需进行一次 CNN 前向传播,分类和回归共享特征,统一优化;区域建议仍依赖外部算法,效率较低。
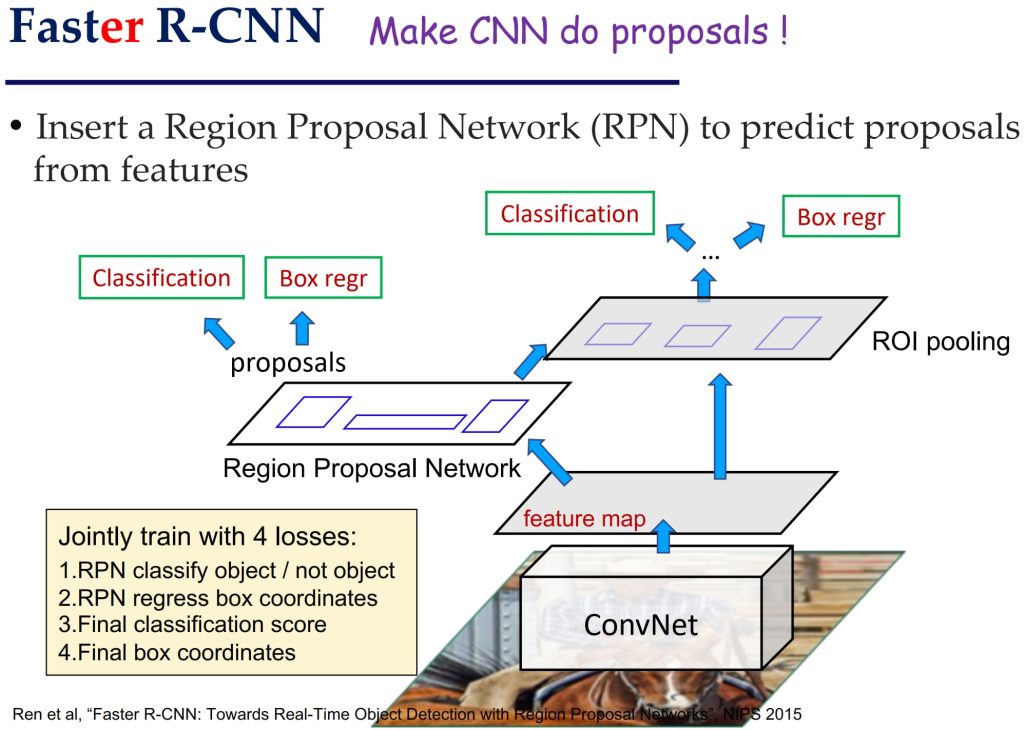
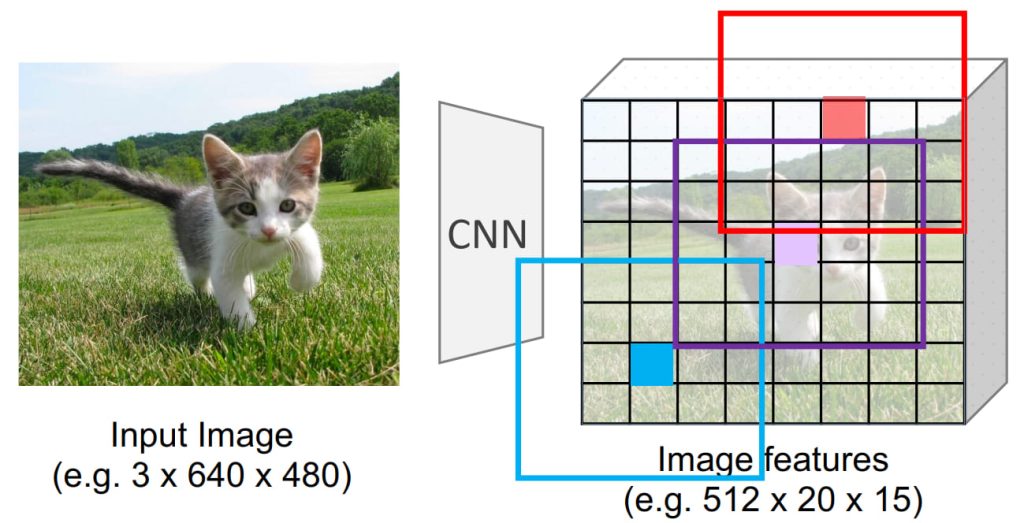
- Faster R-CNN
- 将区域建议与目标检测融合到一个统一网络中,使用 Region Proposal Network (RPN) 直接从特征图中生成候选区域。
- 高效率:区域建议由 CNN 生成,避免使用外部算法;联合训练:RPN 和目标检测共享特征,优化更加高效。
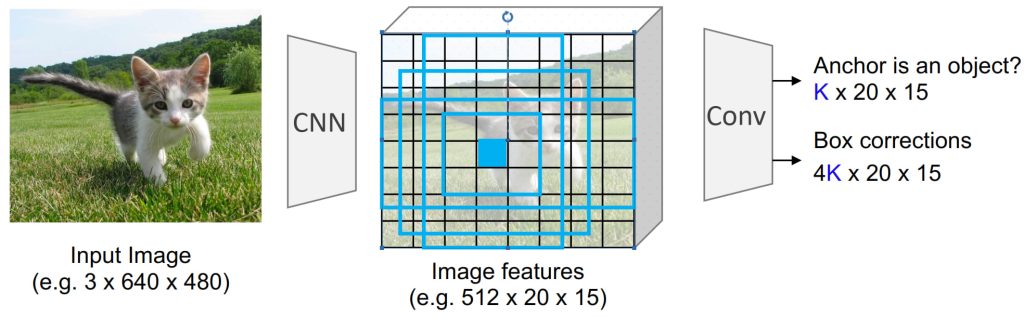
- Region Proposal Network (RPN)
- 在特征图的每个像素位置生成一组 Anchor Boxes,每组具有不同大小和比例。
- 对每个 Anchor Box:分类:是否包含目标,回归:预测边界框的调整。
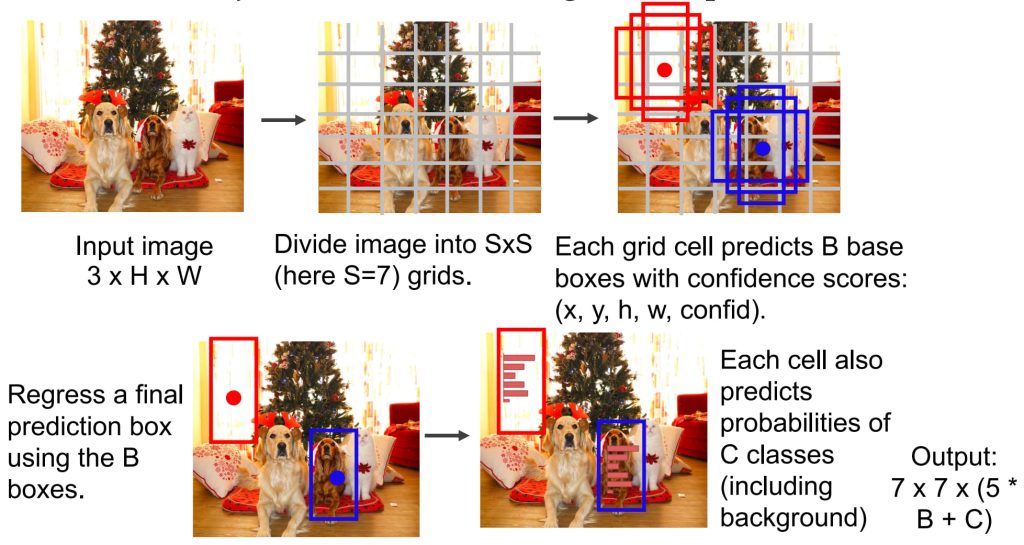
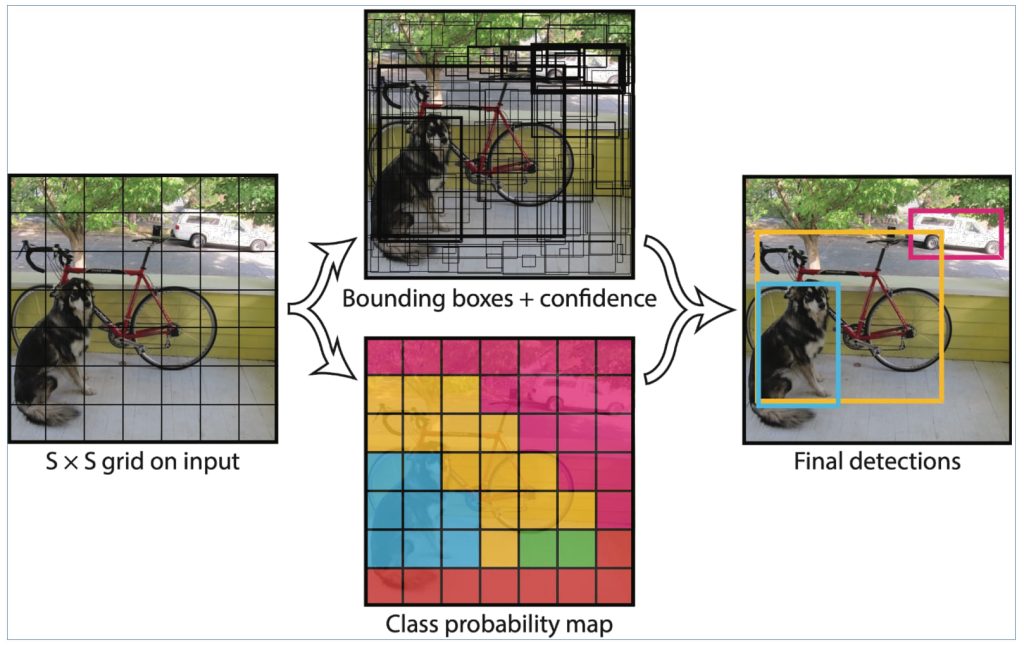
- YOLO (You Only Look Once)
- 将目标检测视为一个单一的回归问题:输入图像直接输出所有目标的类别和边界框;不再依赖区域建议,直接预测目标。
- 实时检测:一次前向传播即可完成所有目标预测;高效率:不需要多阶段处理。对小目标检测效果较差:由于网格划分限制,细粒度目标可能被遗漏;边界框的预测精度较 R-CNN 系列稍低
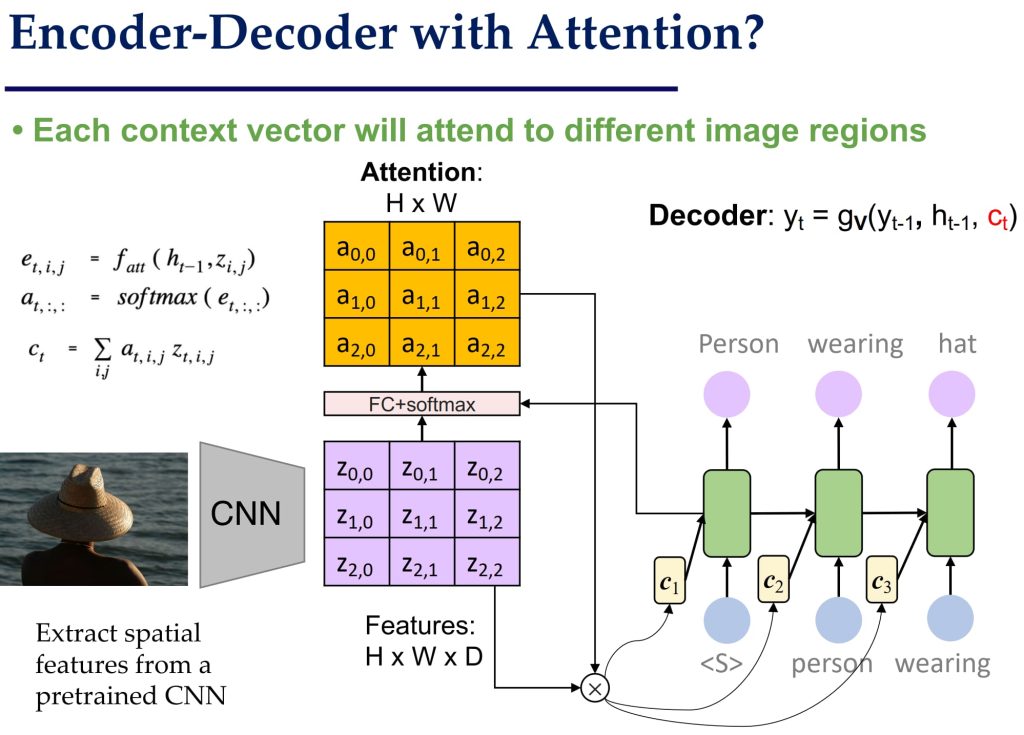
13.3. 图像描述生成(Image Captioning)
- 定义:对一张图片生成自然语言描述。
- 传统 Encoder-Decoder 架构:将图像特征通过 CNN 提取,然后使用 RNN(如 LSTM)作为解码器生成描述。
- 图像特征被压缩到单一的上下文向量(Context Vector),信息可能丢失;无法灵活地关注图像中的不同区域。
- 引入 Attention 机制:在 Encoder-Decoder 架构中加入 Attention,使每个生成的单词可以动态关注图像的不同区域。
- Attention 机制显著提升了生成描述的质量,能够捕捉图像中的局部信息。
- CNN 与 Self-Attention 的结合:将 Self-Attention 应用于 CNN 提取的特征,进一步增强图像特征的表达。
- Self-Attention 模块提高了图像特征的交互性和局部信息的捕捉能力;但仍依赖于 CNN 提取初始特征。
- Transformer 的引入:使用 Transformer 替代传统的 RNN 解码器。
- Transformer 的并行性和长程依赖能力显著提升了文字生成的流畅性。
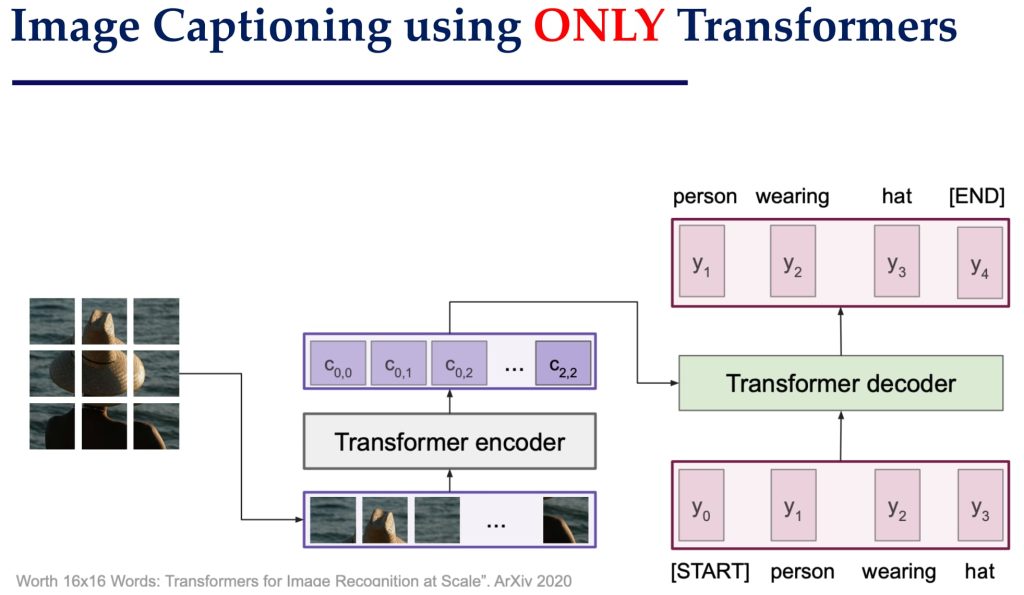
- 完全基于 Transformer 的架构:直接使用 Transformer 提取图像特征并生成描述。
- 将图像划分为网格(Patch),每个网格作为 Transformer 的输入 token;Transformer 的 Encoder 提取图像特征,Decoder 生成文字描述。
- 减少了模型复杂度,避免了 CNN 和 Transformer 功能的重复,可以达到甚至超越 CNN+Transformer 的效果。
13.4. 视觉语言模型(Vision language Models,VLMs)
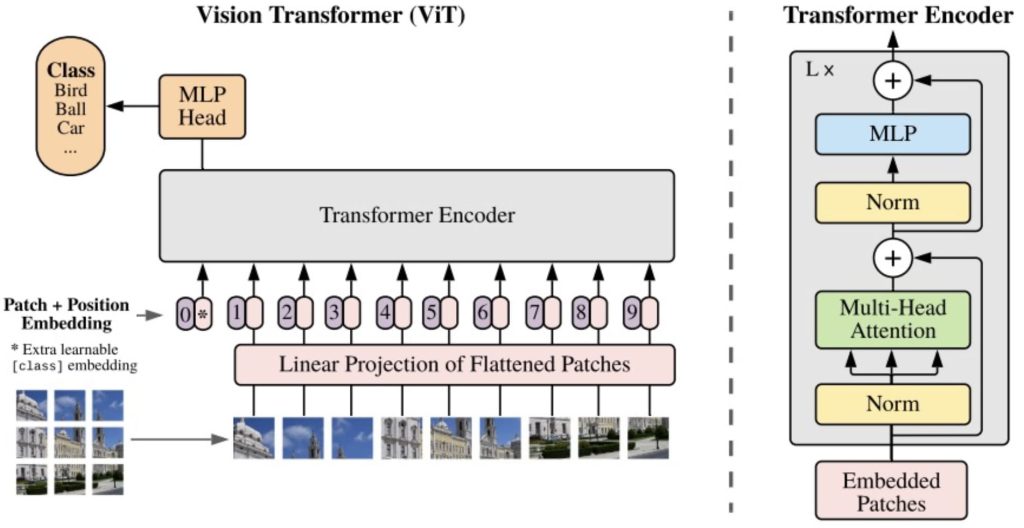
- Vision Transformer(ViT)
- 将图像划分为小的固定尺寸的网格(Patch),每个 Patch 类似于 NLP 中的 Token;使用 Transformer 直接对这些 Patch 进行建模,不再依赖 CNN 提取图像特征。
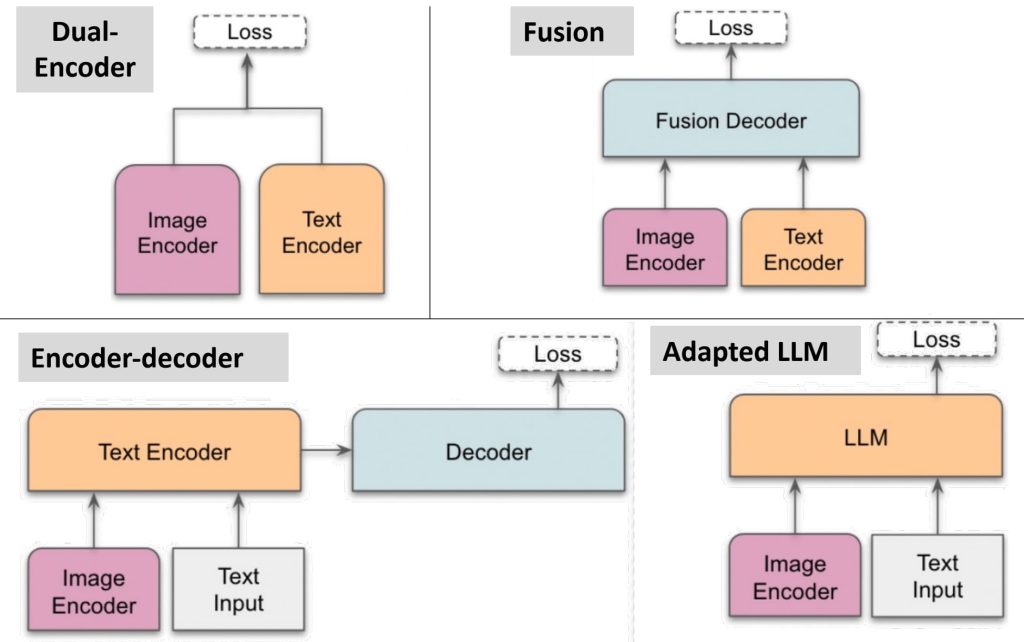
- Contrastive Language-Image Pretraining(CLIP)
- 将图像和文字嵌入到同一个语义空间,通过对比学习实现图文对齐。
- 两个独立的 Encoder(图像 Encoder 和文字 Encoder)分别编码图像和文字;通过对比损失(Contrastive Loss)优化,使匹配的图文对具有更高的相似度。
- LLaVA
- 核心组件:语言模型(如 LLaMA):处理文字输入和生成语言输出;图像编码器(如 CLIP):将图像转换为嵌入向量;投影层(Projection Layer):将图像嵌入映射到语言模型的嵌入空间。
- 流程:图像和文字输入统一转换为嵌入向量;嵌入向量拼接后输入到语言模型,生成目标输出(如回答问题或生成描述)。
14. 聚类(Clustering)(无监督)
- 监督学习(Supervised Learning)
- 目标: 在数据中发现模式,将数据属性与目标(类别)属性关联起来。
- 特点: 数据集提供了明确的标签或目标值,用于训练模型。
- 无监督学习(Unsupervised Learning)
- 目标: 数据没有目标属性。我们希望探索数据以发现其内部结构。
- 特点: 即使没有提供标签,我仍然可以从数据中学习模式。
14.1. 聚类
- 定义: 聚类是一种将无标签数据组织成相似群组(称为簇)的过程。
- 簇(Cluster): 簇是由数据项组成的集合,这些数据项之间“相似”,而与其他簇中的数据项“不同”。
- 相似: 数据项之间的相似性通常通过某种距离度量方法(如欧几里得距离、曼哈顿距离等)来定义。
- 不相似: 数据项之间的距离越大,它们就越不相似。
- 每个簇可以通过一个“中心点”(Centroid)来表示,该中心点代表整个簇。
- 中心点的性质:
- 中心点与簇内的实例比与其他簇的实例更相似;簇内的实例与该簇的中心点比与其他簇的中心点更相似。
- 簇的表示过程:
- 为每个簇选择一个中心点,该中心点能最好地代表簇;每个数据实例被分配一个标签,指示它属于哪个簇。
- 机器学习视角:如何优化“中心-成员关系”?
- 中心更新:簇的中心应该根据簇内实例之间的成对距离来调整,以使中心点更接近簇内数据。
- 标签更新:在获得中心点后,优化每个数据点的“成员关系”(标签),使其分配到最适合的簇。
- 迭代优化:中心更新与标签更新这两个步骤可以交替进行,直到达到收敛(即结果不再显著变化)。
14.2. K-Means
- 核心思想:它将数据划分为 K 个簇;每个簇的中心点(Centroid)定义为该簇中所有数据实例的均值(Mean)。
- 问题定义
- 给定一个数据集 \(D={x_1,\dots,x_N}\),其中每个数据点 \(x_i \in R^d\) 是一个 d-维向量。
- 目标是找到 K 个参考向量(即中心点 \(\mu^k\)),以最佳方式表示 K 个簇。
- 每个数据点 \(x_i\) 被分配一个变量 \(m_i \in {1,\dots,K}\),表示它所属的簇。
- 步骤
- 初始化:随机选择 K 个数据点作为初始的簇中心(称为种子,Seeds)。
- 分配数据点:将每个数据点根据距离分配给与其最接近的中心点(最近簇中心);使用欧几里得距离 \(L_2(x,\mu^k)\) 计算距离。
- 更新中心点:对每个簇,重新计算中心点(均值):\(\mu^k = \frac{1}{C_k} \sum_{x \in C_k} x\),其中 \(C_k\) 是簇 k 的数据点集合。
- 收敛准则 (Convergence Criterion)
- 数据点的重新分配:当数据点在不同簇之间的重新分配为零或最小,即簇分配不再发生显著变化。
- 中心点的变化:当质心(中心点)的位置变化为零或最小,即质心位置趋于稳定。
- 误差的减少:当误差函数(Sum of Squared Error, SSE)的减少达到最小值,SSE 收敛。
- \(\min\limits_{\{\mu^k\}^K_{k=1}} \sum\limits_{k=1}^K \sum\limits_{x \in C_k} L(x – \mu^k)\)
- 时间复杂度 (Time Complexity):
- 计算两个实例之间的距离:O(d),其中 d 是向量的维度;数据点的重新分配:O(knd),其中 k 是簇的数量,n 是数据点的数量;计算质心:O(nd),每个数据点被添加到某个簇。
- 假设以上两步在 I 次迭代中完成:总复杂度为 O(Iknd)。
- 局部最优 (Local Optimum):
- 全局最优:寻找全局最优解是 NP-hard 问题;局部最优:K-means 算法保证收敛到局部最优;不确定性来源:初始质心的选择可能导致不同的局部最优解。
- 对初始质心的敏感性 (Sensitivity to Initial Centroids):
- 初始质心的选择会显著影响聚类结果:随机选择质心可能导致慢速收敛或次优的聚类结果。
- 使用启发式方法或其他算法的结果来选择好的初始质心,如 k-mean++:
- 从数据点中随机选择一个点作为初始质心;对每个数据点 x,计算 D(x),即点 x 到已选质心的最近距离;使用加权概率分布选择新的质心,其中点 x 被选中的概率与 \(D(x)^2\) 成正比;重复步骤 2 和 3,直到选出 k 个质心;使用标准 K-means 算法进行聚类。
- 使用 肘部法则 (Elbow Method)选择簇的数量 k:
- 对每个 k,计算 簇内平方误差和(WSS):\(\text{WSS}=\sum\limits_{i=1}^{m}(x_i−c_i)^2\)
- 绘制 k 和 WSS 的关系图,选择 “肘部”(梯度下降急剧到变缓的转折点)位置的 k 作为最佳值。
- 优势:简单:易于理解和实现;高效:被认为是线性算法,适用于大规模数据。
- 劣势:假设每个簇都是球形;仅适用于定义了均值的情况;用户需要手动指定 k;对异常值(Outliers)敏感。
- 应用:图像分割、图像压缩等。
15. 降维(Dimensionality Reduction)(无监督)
- 维度灾难:随着数据维度的增加,需要更多的数据来准确地进行泛化;数据的维度越高,空间的稀疏性越大,导致模型难以学习分布。
- 降维:目标:减少数据的维度(特征数量),同时保留数据的内在特性;方法:通过发现数据的“隐藏”特性或结构,去除冗余特征,简化数据表示。
- 为什么需要降维:应对数据稀疏性:数据可能本质上存在于更低维的空间中,降维可以解决特征过多但数据不足的问题;降低计算成本:减少内存和时间开销;可视化数据:高维数据降到 2D 或 3D,有助于理解数据分布及其特性;提高模型性能:减少噪声和冗余特征,提高模型的泛化能力。
- 线性方法(Linear Methods):
- 主成分分析 (PCA):找到数据方差最大的方向,用这些方向作为新的特征。
- 线性判别分析 (LDA):用于分类任务,寻找能最大化类间分离的方向。
- 因子分析 (Factor Analysis):识别数据中的潜在因子,解释数据的内在结构。
- 非线性方法 (Non-linear Methods):
- 核主成分分析 (KPCA) 和 核线性判别分析 (KLDA):使用核函数处理非线性数据。
- 多维尺度法 (MDS):保留数据点之间的距离关系。
- t-SNE:非线性降维技术,保留局部数据结构,适用于可视化。
- 自动编码器 (Autoencoder):使用神经网络实现非线性降维。
15.1. 主成分分析(Principal Component Analysis,PCA)
- 核心思想:一种线性降维技术,用于发现数据中具有最大方差的方向(主成分);目标是将高维数据投影到较低维的子空间,同时尽可能保留数据的主要信息。
- 步骤:
- 数据预处理:将数据中心化,使其均值为零;
- 计算协方差矩阵 \(S = \frac{1}{N} X X^T\);
- 对协方差矩阵 S 进行特征值分解,并根据特征值大小对特征向量进行排序;
- 确定新空间的维度 k;
- 选择具有最大 k 个特征值的特征向量作为新空间的基。
- 选择维度 k:
- 通过保留特征值的累计方差来决定 k:\(\text{信息损失} = \frac{\lambda_{k+1} + \lambda_{k+2} + \dots + \lambda_d}{\lambda_1 + \lambda_2 + \dots + \lambda_d}\),通常限制信息损失在 5% 以下。
- 总而言之,PCA 旨在解决一个二次规划的约束最优化问题,是一种凸优化问题,S 是正半定矩阵(positive semi-definite \(x^TAx \ge 0 , \ A = A^T\))。
- \(\text{max}_u \mathbf{u}^T\mathbf{S}\mathbf{u}, \ s.t. \mathbf{u}^T\mathbf{u} = 1\)
- 应用:数据可视化,数据预处理,建模 – 为新数据设定先验,数据压缩,人脸识别
示例:
- 以数据为例:\(A = [2.5, 2.4],B = [0.4, 0.7],C = [2.2, 2.9]\)
- 计算样本均值及协方差矩阵:
- \(\bar{x} = \begin{bmatrix} \frac{2.5 + 0.4 + 2.2}{3} & \frac{2.4 + 0.7 + 2.9}{3} \end{bmatrix} = \begin{bmatrix} 1.7 & 2 \end{bmatrix}\)
- 定义协方差及协方差矩阵(以2维为例,若三维则为xyz),(n为样本数量)
- \(\text{cov}(X, Y) = \frac{\sum_{i=1}^{n}(X_i – \bar{X})(Y_i – \bar{Y})}{n – 1}\)
- \(S_{n \times n} = \begin{bmatrix} \text{cov}(x, x) & \text{cov}(x, y) \\ \text{cov}(y, x) & \text{cov}(y, y) \end{bmatrix}\)
- 例子中:
- \(\text{cov}(x, x) = \frac{(2.5 – 1.7)^2 + (0.4 – 1.7)^2 + (2.2 – 1.7)^2}{3 – 1} = 1.26\)
- \(\text{cov}(x, y) = \text{cov}(y, x) = \frac{(2.5 – 1.7)*(2.4 – 2) + (0.4 – 1.7)*(0.7 – 2) + (2.2 – 1.7)*(2.9-2)}{3 – 1} = 1.23\)
- \(\text{cov}(y, y) = \frac{(2.4 – 2)^2 + (0.7 – 2)^2 + (2.9-2)^2}{3 – 1} = 1.33\)
- \(S = \begin{bmatrix} 1.26 & 1.23 \\ 1.23 & 1.33 \end{bmatrix}\)
- 解协方差矩阵 S 的特征值 \(\lambda\),即 \(|S – \lambda I| = 0\) 的解:
- \(|S – \lambda I| = \begin{vmatrix} 1.26 – \lambda & 1.23 \\ 1.23 & 1.33 – \lambda \end{vmatrix} = (1.26 – \lambda)(1.33 – \lambda) – 1.23^2 = 0\)
- 解得 \(\lambda_1 = 0.06, \quad \lambda_2 = 2.53\)
- 进而得到与 \( \lambda \) 对应的特征向量,特征向量满足:\(Sv = \lambda v, (S – \lambda I)v = 0\)
- 需要求 v=[x, y],然后需输出 x, y 的比例,再归一化得到单位长度:
- 对于 \(\lambda_1 : \ \begin{bmatrix} 1.26 – 0.06 & 1.23 \\ 1.23 & 1.33 – 0.06 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\)
- 得 \(\frac{x}{y} = \frac{-1.23}{-1.2} \approx -1.27\)
- 以上两个约等于是因为计算误差导致的,实际上会是一个值,再进行归一化:\(v_1 = [0.713, -0.696]\)
- \(\lambda_2\) 同理,\(v_1 = [0.696, 0.713]\)(因为是二维所以可以直接看出来,三维不行)
- 两个主成分的表示:
- \(F_1 = v_{11}(x – \bar{x}) + v_{21}(y – \bar{y}) = 0.713(x – 1.7) – 0.696(y – 2)\)
- \(F_2 = v_{12}(x – \bar{x}) + v_{22}(y – \bar{y}) = 0.696(x – 1.7) + 0.713(y – 2)\)
- 主成分的贡献度p:(经证明主成分的方差就是特征值大小)\(p_i = \frac{\lambda_i}{\sum \lambda_i}\)
- 对于示例:
- \(F_1 \text{贡献度} = \frac{0.06}{0.06 + 2.53} \approx 0.02\)
- \(F_2 \text{贡献度} = \frac{2.53}{0.06 + 2.53} \approx 0.98\)
- 可以根据贡献度从大到小,对所有主成分进行排序,然后根据累计贡献度要求选出前几个主成分
15.2. PCA = 神经网络 = 自编码器(Auto-encoder)
- PCA(主成分分析)——另一种视角
- PCA通过基本组件(如\(u_1,u_2,\dots\))的线性组合来近似输入数据,从而实现数据压缩。
- 输入数据可以表示为:\(x \approx z_1\mathbf{u}_1 + \dots | z_k\mathbf{u}_k + \bar{x}\),其中 \(z_1, z_2, \dots, z_k\) 是低维特征表示。
- PCA = 神经网络
- PCA等效于一个带有单隐藏层的神经网络(线性激活),目标是最小化重构误差。
- 它通过优化(最小化重建误差) \(z_j = (x – \bar{x}) \cdot u_j\),将高维数据降维,生成低维嵌入表示。
- PCA = 自编码器(Auto-encoder)
- 自编码器是一种神经网络,包含编码器和解码器,目标是重构输入数据。
- 编码器将输入数据压缩到低维表示 z,解码器尝试从 z 重构原始数据。
- 深度自编码器(Deep Auto-encoder)
- 深度自编码器通过瓶颈隐藏层(Bo-leneck hidden layer)强制网络学习压缩的低维表示,得到潜在编码(Latent code)z ,同时通过重构损失使重构尽可能接近输入。
- 与PCA相比,深度自编码器可以捕获非线性特征,效果更强。
- 自编码器的应用:
- 图像搜索:使用自编码器的压缩表示(如256维特征)进行图像检索,比直接在像素空间检索更高效。
- 去噪自编码器(Denoising Auto-encoder):接收损坏的输入数据,训练网络预测原始数据,从而去除噪声。
- 基于CNN的自编码器:使用卷积神经网络(如U-Net架构)进行图像压缩和重构,适用于复杂图像数据。
16. 深度生成式模型(Deep Generative Models)(无监督)
- 回顾语言模型:一个关于给定字符串在某种“语言”中出现概率的概率模型。
- 生成:学习训练数据的概率分布;将图像作为 x 一个高维向量(例如 64×64×3 维的向量),使用概率密度函数评估图像在数据分布中的出现可能性。
生成式模型:
- 目标:生成模型的目标是找到一个概率分布 p_model(x),使其能够很好地逼近真实数据分布 p_data(x)。
- 如何表示 p_model(x):
- 使用生成器 (Generator, G),通常是一个神经网络,将随机噪声 Z∼N(0,1) 转化为复杂的分布 p_G(x),使生成的图像尽可能接近真实数据分布 p_data(x)。
- 如何实现 p_model(x) 接近 p_data(x):
- 使用判别器 (Discriminator, D),一个神经网络分类器,用于区分图像是否来自真实数据分布 p_data(x) 或生成器分布 p_model(x),如果判别器无法区分两者,则说明 p_model(x) 接近 p_data(x)。
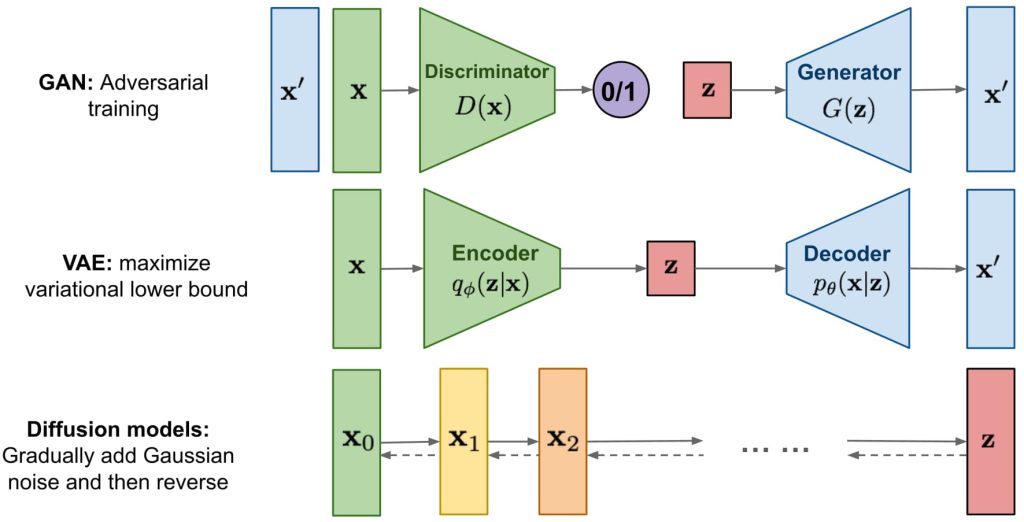
16.1. 生成式对抗网络(Generative Adversarial Network,GAN)
- 一种通过让两个神经网络相互对抗来实现的生成模型。
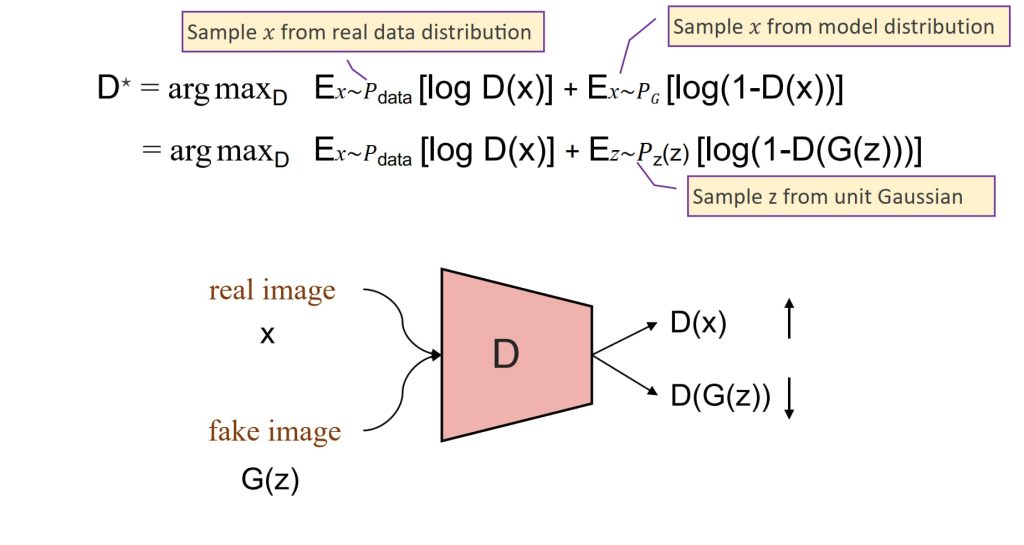
- 判别器(D)的目标:
- 需要将真实图像(来自数据分布)分类为“真实”(输出接近1),生成器生成的虚假图像分类为“虚假”(输出接近0)。
- 其目标函数基于二元交叉熵损失,通过最大化正确分类的对数概率来优化。
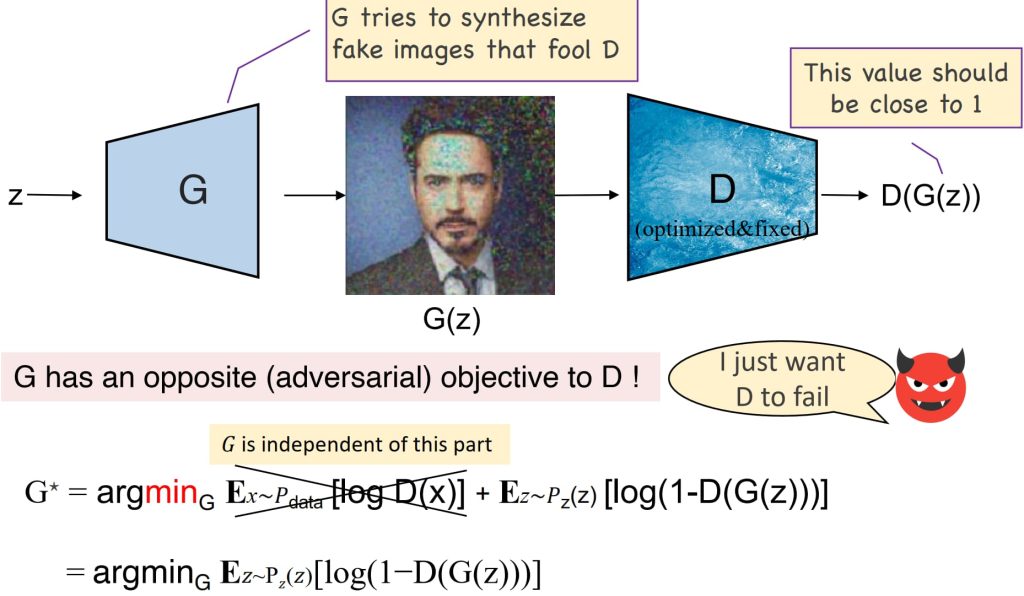
- 生成器(G)的目标:
- 生成能够欺骗判别器,使其将虚假图像分类为“真实”的数据。
- 最小化判别器正确分类虚假图像的能力,与判别器对抗,旨在优化虚假图像被分类为“真实”的概率。
- GAN的整体目标:
- 形成一个最小最大游戏,其中生成器尝试最小化损失,而判别器尝试最大化损失。
- 在全局最优状态下,生成器能够复现真实的数据分布,而判别器对真实和虚假图像的输出变得不可区分。
- \(\min\limits_G \max\limits_D V(G, D) = E_{x \sim P_{data}}[\log D(x)] + E_{z \sim P_z(z)}[\log(1 – D(G(z)))]\)
- 需要注意的是,训练开始时,需要有一个已经预训练过的判别器,否则训练结果不好。

16.2. Deep Convolutional GANs (DCGAN)
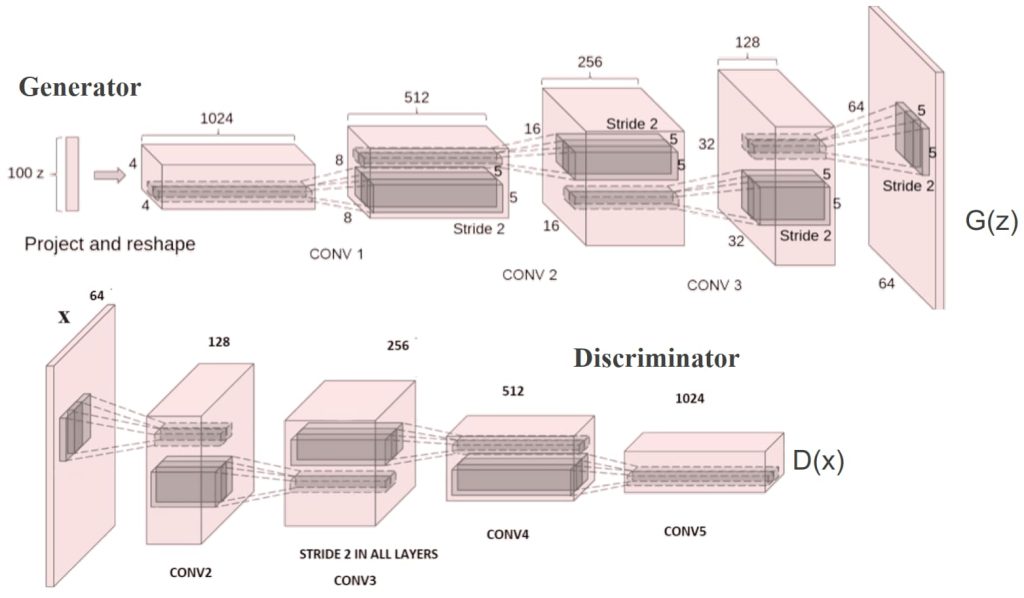
- 使用卷积(Convolution)和反卷积(Deconvolution)分别构建判别器(Discriminator)和生成器(Generator)。
- 改善了传统GAN的架构,使其更适合处理图像数据。
- 使用潜向量(Latent Vector)进行插值或操作,例如人脸的加减运算(通过对不同特征的人脸图像叠加可以生成指定特征的图像)。
16.3. Conditional GANs (CGAN)
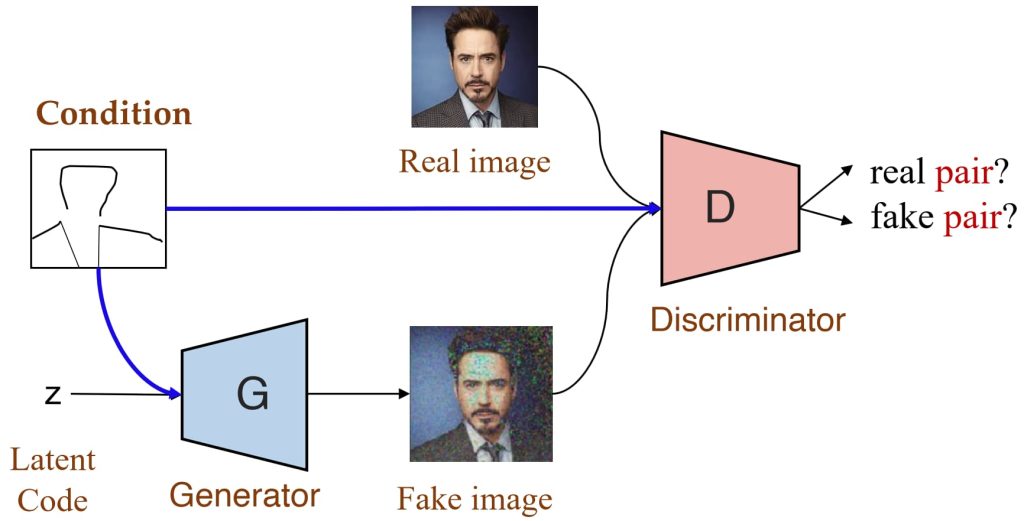
- 可以通过给定条件(例如标签)控制输出图像的性质。
- 判别器不仅判断图像真假,还判断图像是否与条件匹配。
- 应用:图像到图像翻译(Image-to-Image Translation)。
- 局限:需要监督学习(Supervised Learning)并依赖于成对的图像。
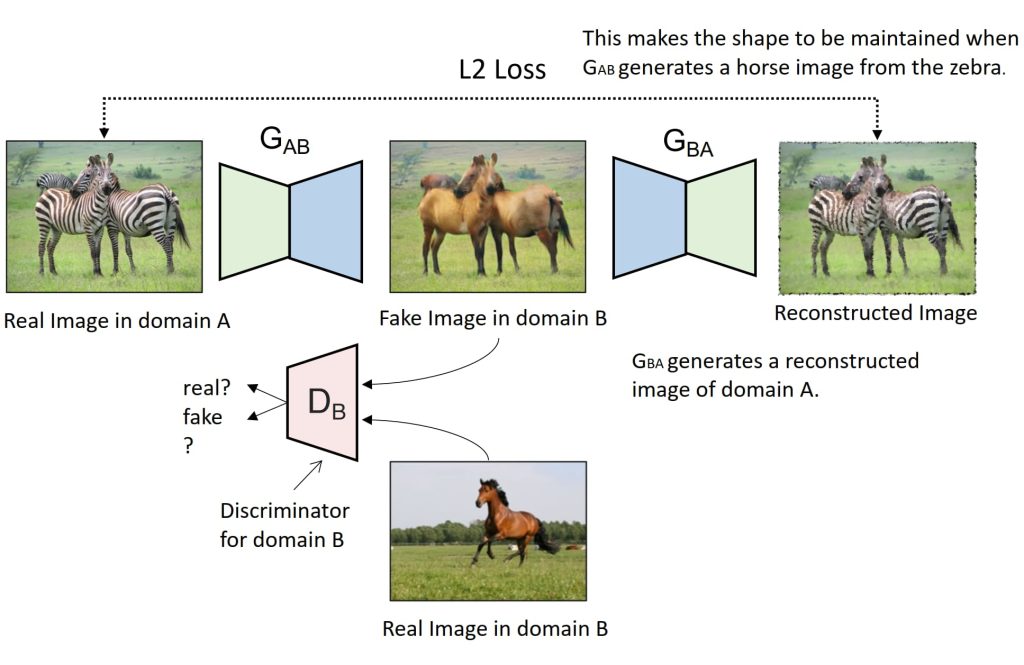
16.4. CycleGAN:图像域转换(Domain Transformation)
- GAN 本质上是一个从随机分布到图片概率分布的概率转换器;而 CycleGAN 需要的是从图片概率分布到图片概率分布的概率转换器
- 支持无监督学习,能够在没有配对样本的情况下进行图像域转换(Domain Transformation)。
- 通过循环一致性损失(Cycle Consistency Loss)确保转换后的图像能够恢复到原始域。
- 应用:将一个领域(Domain A)的图像转换为另一个领域(Domain B)。
- 工作机制:
- 使用生成器 G_AB 将域A的图像转换为域 B。
- 使用生成器 G_BA 将域B的图像转换回域 A。
- 使用循环一致性损失(L2 Loss)确保转换后的图像能够恢复原始。
16.5. 变分自编码器(Variational Autoencoder,VAE)
- 一种概率版的自编码器,其中潜在编码 z 是从编码器预测的高斯分布 (z∼N(μ,σ)) 中采样得到的,以确保潜在空间的平滑性和结构性。
- 组成部分:编码器:将输入 x 映射到高斯分布的均值 (μ) 和标准差 (σ);解码器:从潜变量 z 生成输出 x_gen。
- 训练问题:采样过程不可微分。
- 解决方案:使用重参数化技巧 (Reparameterization Trick),梯度可以在采样过程中正常传播,以实现反向传播。
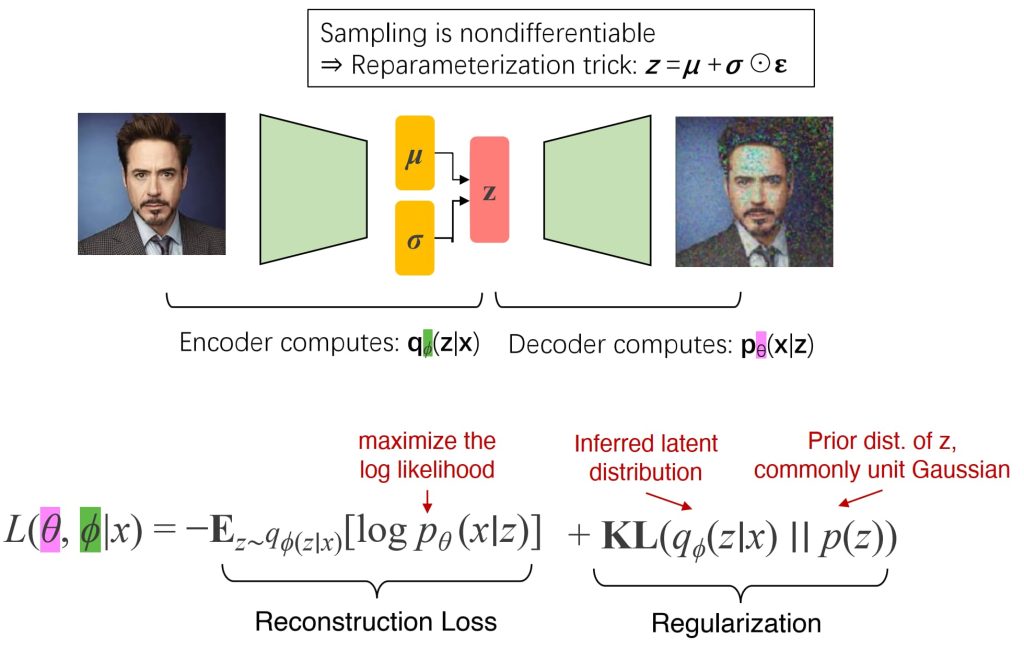
- 目标函数:损失函数包含两部分:重构损失(最大化重构 x 的可能性)+正则化(KL散度,对 q(z|x)进行正则化,使其逼近先验分布(如单位高斯分布)).
- 正则化(Regularization)的作用:确保潜在空间的平滑性和结构性
- 连续性:潜在空间中相近的点解码后应生成相似的内容。
- 完整性:从潜在空间中采样应始终生成有意义的解码内容。
- 效果:z 的不同维度可以编码不同的可解释特征(例如笑容、头部姿态),对单一潜变量进行扰动会导致生成图像中特定特征的逐渐变化。
- VAE(和GAN)的局限性
- 潜在空间的大小:z 的维度比原始图像 x 的维度小得多。
- 生成过程:内容是一次性生成的,而不是逐步生成(例如从粗到精)。
16.6. 去噪扩散模型(Denoising Diffusion Model)
- 定义:通过逐步去除噪声来生成数据。其核心思想是从完全随机的噪声开始,通过学习逆过程逐渐生成清晰的图像。两个核心过程:正向扩散过程和反向去噪过程
- 正向扩散过程 (Forward Diffusion Process)
- 目标:逐步向数据添加噪声,使原始数据 \(x_0\) 转化为完全随机的噪声 \(x_T\)。
- 噪声添加过程是固定的,通过高斯分布逐步实施。
- \(q(x_t | x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 – \beta_t} x_{t-1}, \beta_t \mathbf{I})\)
- \(\text{Let } \bar{\alpha}_t = \prod_{s=1}^t (1 – \beta_s) \rightarrow x_t \sim q(x_t | x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 – \bar{\alpha}_t) \mathbf{I})\)
- 反向去噪过程 (Reverse Denoising Process)
- 目标:逐步去除噪声,从噪声 \(x_T\) 恢复到数据 \(x_0\)。
- 反向过程是可训练的,通过神经网络学习去噪的步骤。
- \(p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \sigma^2_t \mathbf{I}) \quad p(x_T) = \mathcal{N}(x_T; \mathbf{0}, \mathbf{I}) \)
- 其中 N 是可训练的网络(U-net, Denoising Autoencoder)。
- 损失函数:
- 目标是学习(一个参数化数据分布均值的网络):\(p_\theta(x_{t-1} | x_t) = \mathcal{N}(x_{t-1}; \mu_\theta(x_t, t), \Sigma_\theta(x_t, t))\)
- 因此最小化 \(\text{MSE}(\mu_\theta(x_t, t), x_{t-1})\)
- 神经网络架构:
- 通常使用 U-Net 结构,结合 ResNet块 和 自注意力层。
- 神经网络预测噪声 \(\bm{\epsilon}_\theta(x_t, t)\),然后计算去噪的均值 \(\bm{\mu}_\theta(x_t, t)\)。
- 去噪的均值公式为:\(\bm{\mu}_\theta(x_t, t) = \frac{1}{1 – \beta_t} \left( x_t – \frac{\beta_t}{\sqrt{\alpha_t}} \bm{\epsilon}_\theta(x_t, t) \right)\)

17. 强化学习(Reinforcement Learning)
17.1. 基于马尔可夫决策过程(MDP)的问题建模
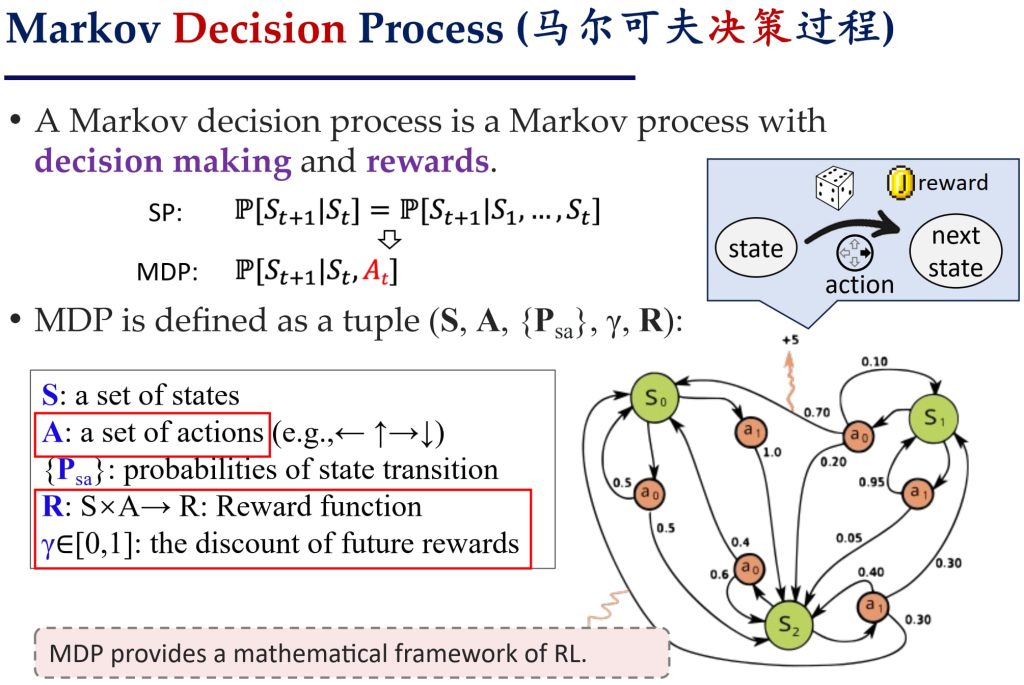
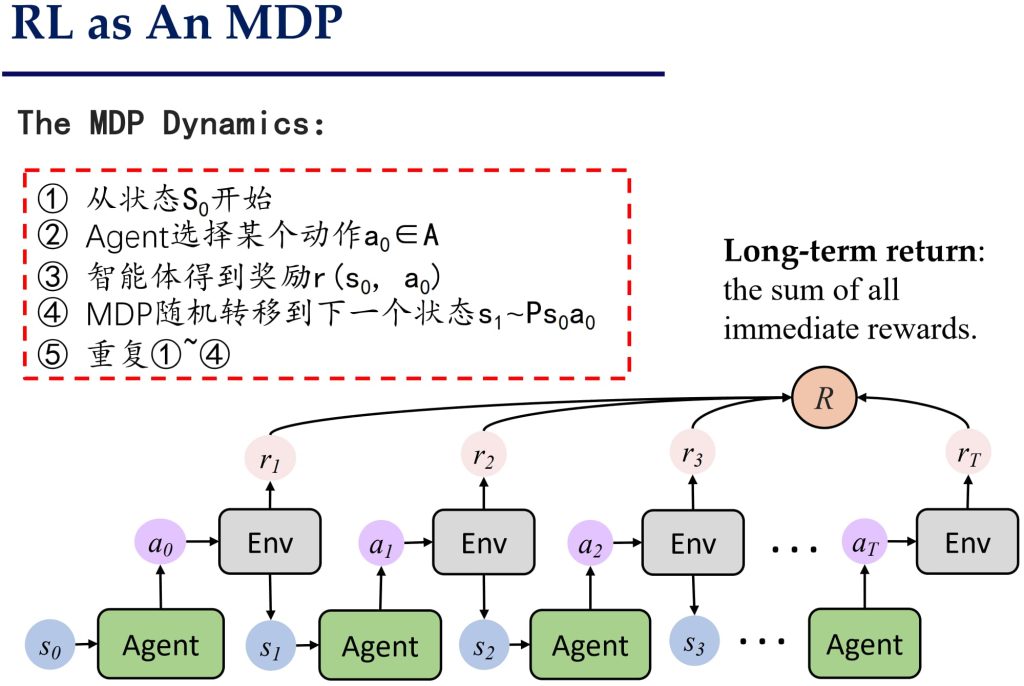
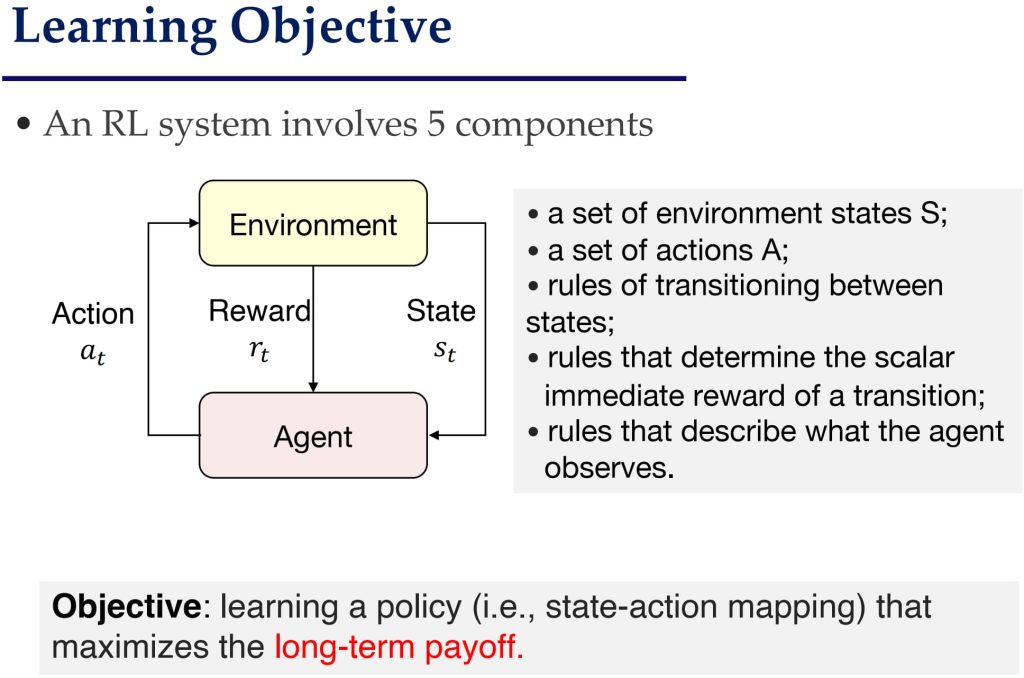
- 目标:学到一个策略(即状态到动作的映射关系),使得在每个状态下选择的动作能够最大化长期回报。
- 学习过程:智能体在状态空间中寻找一条路径,使得累积回报最大化。
- 核心问题:如何再每个状态下选择最佳动作
- 实际长期回报:\(R_t = \sum_{i=t}^\infty r_i\)
- 折扣长期回报:\(R_t = \sum_{i=t}^\infty \gamma^{i-t} r_i\)
- 其中:R_t 表示从时间 t 开始的长期回报。r_i 表示在时间 i 时获得的即时奖励。γ 是折扣因子,γ ∈ [0,1]。
17.2. Q-Learning
- Q-函数 Q(s,a) 表示在状态 s 下选择动作 a 后,预期的总未来奖励。公式为:
- \(Q(s_t, a_t) = \mathbb{E}[R_t | s_t, a_t]\),其中 \(R_t\) 是时间 t 开始的回报
- 最优策略 π∗(s) 是选择使得 Q(s,a) 最大化的动作:\(\pi^*(s) = \arg\max_a Q(s, a)\)
- Q-learning 通过构建 Q(s,a) 的表来学习状态-动作对的评分。更新规则为:
- 将未初始化的状态-动作值 Q(s,a) 设为 0,并加入 Q 值表。
- 以概率 p 选择 Q 值最大的动作 a(否则随机选择 a)。
- 执行动作 a,并获得即时奖励 r。
- 更新 Q(s,a) 的值:\(Q(s, a) \leftarrow r + \gamma \max\limits_{a’} Q(s’, a’)\),其中 r 是即时奖励,γ 是折扣因子,s′ 是下一状态。
- 将状态更新为 s’。
- 如何得到Q值:
- 蒙特卡洛:通过遍历后续所有情况/随机计算几种后续情况,计算平均的奖励值;但是会耗费大量时间。
- 递归估计:根据递推关系,采用动态规划的方式,填写一个Q值表,直至表填满(递归关系不唯一)。
- 问题:
- Q-learning 的主要问题是状态空间过大。当状态空间涉及 N 个二进制变量时,表的大小为 2的N次方。如果每个维度有 k 个值,则表大小为 k的N次方。
17.3. Deep Q Networks(DQN)
- 核心思想:
- 使用深度神经网络(如CNN)来逼近强化学习中的Q函数。
- 状态 + 动作 → 期望回报:网络预测给定状态和动作的Q值。
- 状态 → 所有动作的Q值:网络可以预测当前状态下所有动作的Q值,从而选择最佳动作。
- 训练过程:
- 输入:当前状态 \(s_t\) 和动作 \(a_t\)。输出:预测的Q值 \(Q_θ(s_t,a_t)\)。
- 目标 Q 值:\(\mathbb{E}(R_t | s_t, a_t) = r_t + \gamma \text{max}_aQ_θ(s_{t+1},a)\)
- 损失函数,最小化预测的Q值与目标Q值之间的均方误差(MSE):
- \(\ell \left( \theta \mid s_t, a_t, r_t \right) = \| \underbrace{\left( r_t + \gamma \max_a Q_\theta \left( s_{t+1}, a \right) \right)}_{{\text{target}}} – \underbrace{Q_\theta \left( s_t, a_t \right)}_{{\text{predicted}}} \|^2\)
- 训练步骤:使用梯度下降更新参数 θ,以最小化损失函数。
- 数据与目标:
- 采集数据:通过与环境交互,收集状态转移数据 \((s_t,a_t,r_t,s_{t+1})\)。
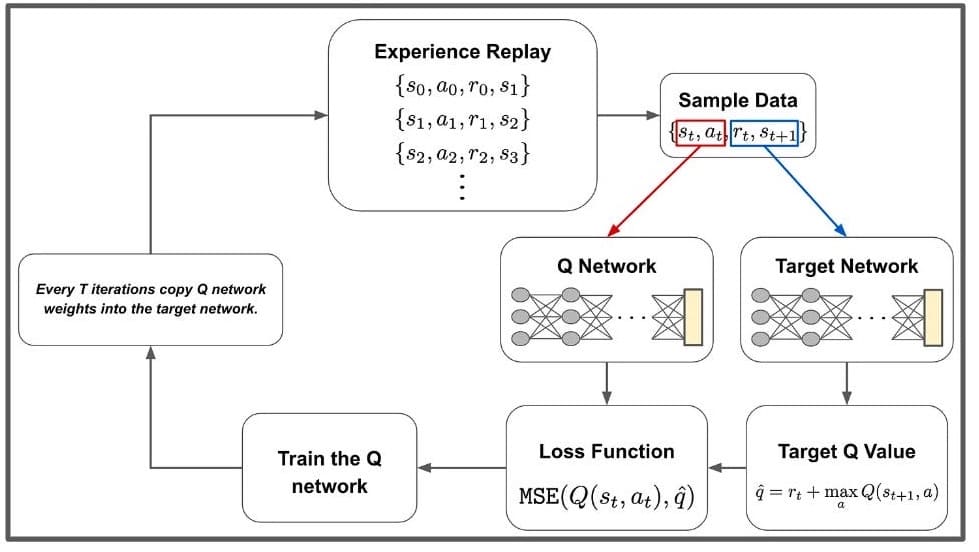
- 经验回放 (Experience Replay):将采集的转移数据存储到回放记忆库中;从记忆库中随机采样小批量数据,打破数据之间的相关性,提升训练稳定性。
- 对于一个批量数据 (s,a,r,s′),损失函数为:
- \(L \left( \theta \mid D \right) = \mathbb{E}_{(s, a, r, s’) \sim \mathcal{D}} [ \| \underbrace{\left( r + \gamma \max_a Q_\theta \left( s’, a’ \right) \right)}_{\text{target}} – \underbrace{Q_\theta \left( s, a \right)}_{\text{predicted}} \|^2 ]\)
- 训练DQN:
- 问题:Q目标值依赖于网络参数 θ,而 θ 会不断更新,导致训练不稳定。
- 解决方案:固定Q目标:使用一个单独的“目标网络”,其参数 θold 固定,仅每隔 C 步更新一次。
- \(\nabla_{\theta_t} L = \mathbb{E}_{(s, a, r, s’) \sim D} [ \underbrace{( r + \gamma \max_{a’} Q(s’, a’; \theta_{\text{old}})}_{\text{fixed, old Q-target}} – Q(s, a; \theta_t) ) \nabla_{\theta_t} Q(s, a; \theta_t) ]\)

17.4. 策略梯度(Policy Gradient)
- DQN(Deep Q-Network):使用 Q 函数来估计动作价值,并通过 π*(s) = argmax_a Q(s, a) 推导最优策略;使用深度神经网络(DNN)来近似 Q 函数。
- Policy Gradient:直接优化策略 π(s);使用 DNN 预测动作概率 P(a|s),选择动作 a_1 的概率最大。
- 训练过程:
- 目标:使用深度神经网络(DNN)建模策略 π_θ。网络输入:状态 s_t。网络输出:动作概率分布 Pθ(a|s)。
- 训练:估计参数 θ,使得策略 π_θ 的性能提高(通过交互经验训练)。
- 测试:根据策略分布 a ~ P_θ(a | s) 选择动作。
- 数据与目标:
- Episode:执行策略 π_θ,,直到终止,记录轨迹 \(τ = (s_1, a_1, r_1, s_2, a_2, r_2, …, s_T, a_T, r_T)\);总奖励 \(R(τ) = r_1 + \gamma r_2 + \gamma ^2r_3 + … + \gamma ^(T-1)r_T\)。
- 学习目标:运行多个轨迹 \(τ^{(1)}, τ^{(2)}, …, τ^{(N)}\) 以估计期望奖励 \(R_θ = \mathbb{E}_{\tau~p(\tau)}R(\tau)=\sum_{\tau}R(\tau)p_{\theta}(\tau)\)。
- 目标是最大化 \(R_{\theta}\),通过梯度更新参数 \(\theta \leftarrow \theta + \eta \nabla_{\theta}R_{\theta}\)。


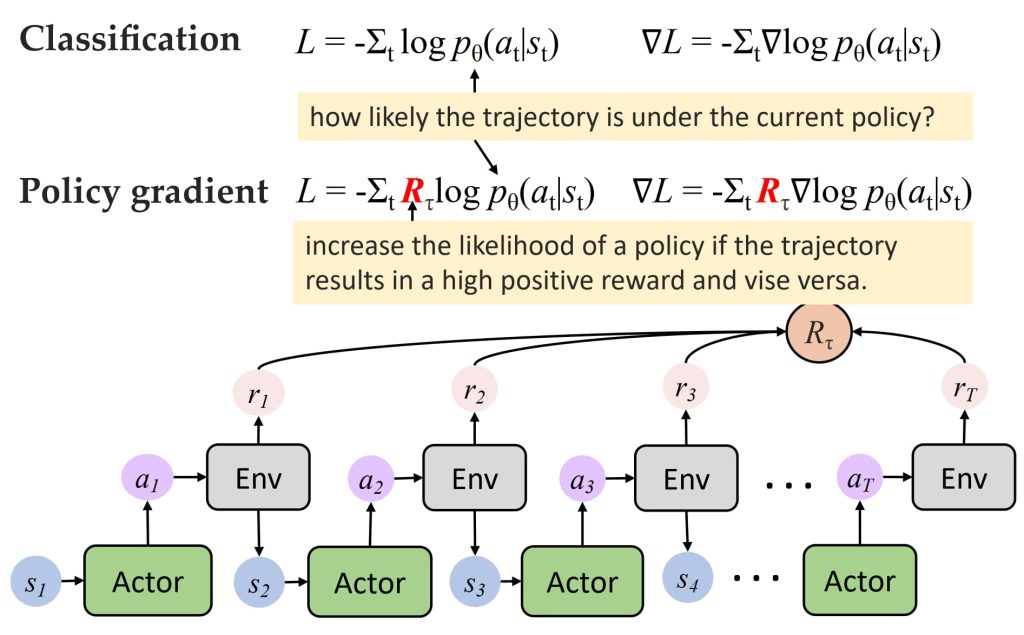
- Policy Gradient vs Classification
- 分类任务:关注轨迹在当前策略下的概率。
- Policy Gradient:增加奖励高的轨迹概率,减少奖励低的轨迹概率。
17.5. 蒙特卡洛树搜索(Monte-Carlo Tree Search,MCTS)
- Selection(选择):根据当前树结构选择最优路径。
- 策略:选择节点时综合考虑 Q (动作价值) 和 u(P) (探索值),公式: Q + u(P);u(P) 与节点的 访问次数 N 和 先验概率 P 成反比。
- Expansion(扩展):在树中扩展新的节点。
- 策略:使用 Policy Network (策略网络) 提供 P (先验概率),生成可能的动作;每次扩展一个或多个子节点。
- Evaluation(评估):评估新扩展节点的价值。
- 使用 Value Network (价值网络) 来估算新节点的状态价值 Vθ。
- Rollout(预演/模拟):使用随机策略或简单策略模拟游戏结果。
- 从当前节点开始模拟游戏,直到终局;返回游戏得分 r 和价值网络评估 Vθ。
- Backup(回溯):将模拟结果回溯更新到树的所有相关节点。
- 更新动作价值 Q;综合 Vθ (价值网络评估) 和 r (游戏得分),影响父节点的估值。
17.6. 强化学习在文本生成中的应用 (RL for Texts)
- 回顾 NLG(Neural Language Generation):
- 使用 Ground-Truth 数据指导模型生成。
- 目标: 最小化交叉熵 (最大化似然) \(\mathcal{L}(\theta | x, y) = – \sum_{t=1}^{T} \log p_\theta (y_t | y_{1:t-1}, x)\)
- MLE(Maximum Likelihood Estimation,最大似然估计)训练的问题
- 训练目标和测试目标不一致:训练: 最大化预测词的似然,偏向短期优化;测试: 关注对话的正确性、连贯性、流畅性、多样性,偏向长期优化。
- 深度强化学习模型 (Deep Reinforced Model for NLG)
- 目标:学习一个策略,使生成的文本能够最大化长期目标。
- 核心组件:States:编码器的隐藏状态和之前的输出;Actions:生成或复制一个词 y∈V;Rewards:质量指标 (BLEU, ROUGE, DISTINCT 等),有意义性、人类化等;Policy:决定在每个状态下生成哪个词。
- 训练:使用策略梯度优化目标函数,最大化奖励 R。
- 损失函数:\(\mathcal{L}(\theta) = -\sum_{t=1}^{T} R \log p_\theta (\hat{y}_t | \hat{y}_{1:t-1}, x)\)
17.7. RLHF(Reinforcement Learning from Human Feedback)
\(\text{Pre-Training} \rightarrow \text{SFT} \rightarrow \text{RLHF} \overset{\scriptsize \text{Fine-Tuning}}{\underset{\scriptsize \text{In-Context Learning}}{\rightarrow{}}} \text{Downstream Application}\)
- Supervised Finetuning(SFT)
- 目标:优化 LLM,使其能够生成用户期望的回复。
- 方法:使用人工标注的提示-回答对(prompt-response pairs)来微调初始语言模型;人工编写的回答能够帮助模型学习如何生成高质量的输出。
- 过程:输入:提示和文本数据集;输出:使用人类增强的文本对模型进行微调,生成更准确的初步模型。
- Create a Reward Model(RM)
- 目标:优化 LLM,使其能够生成用户期望的回复。
- 方法:使用 SFT 阶段微调后的模型生成候选回复;人类对这些回复进行排序(标注偏好),以形成排序数据;训练奖励模型,使其能够根据人类偏好输出奖励分数。
- 过程:输入:提示数据集和模型生成的候选回复;输出:奖励模型能够对生成的回复进行打分,反映人类偏好。
- Finetuning via Reinforcement Learning(RLHF)
- 目标:优化 LLM,使其能够生成用户期望的回复。
- 方法:使用奖励模型的分数作为强化学习的奖励信号;采用近端策略优化算法(PPO)来更新模型参数;在优化过程中会加入一个 KL散度惩罚项,以防止模型偏离初始 SFT 模型的分布过远。
- 过程:输入:SFT模型、奖励模型及提示数据集;输出:最终微调后的语言模型,能够更好地生成符合人类偏好的回复。